| ArcGIS数字线划图坐标转换实现与精度分析 |
全面启用2000国家大地坐标系后,在过渡期内需要将现有1954年北京坐标系、1980西安坐标系下测绘成果逐步转换到2000国家大地坐标系。转换内容包含控制点成果资料,以及数字线划地图、数字栅格地图、数字正射影像图、数字高程模型4D测绘产品。其中数字线划图格式复杂、数据量较大,因此研究数字线划图的坐标转换方法,通过研制坐标转换软件实现自动化批量转换,是加快2000国家大地坐标系推广使用需要解决的一项重要工作[1-3]。
ArcGIS软件广泛应用于城市规划、土地管理、地质、矿产等领域,多个行业内的大量图件均需要实现原有坐标系向2000国家大地坐标系的转换工作[4, 5]。
1 坐标转换方法 1.1 二维4参数转换模型对于小范围坐标转换,图件数据一般仅存储二维平面坐标信息,大多采用平面四参数模型。通过选取一定数目的公共点数据,求解平面4参数,最终根据求解获得的4参数完成坐标转换。
| $ \left[ {\begin{array}{*{20}{c}} {{x_2}}\\ {{y_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta {x_0}}\\ {\Delta {y_0}} \end{array}} \right] + \left( {1 + m} \right)\left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha }\\ {\sin \alpha }&{\cos \varepsilon } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{y_1}} \end{array}} \right] $ | (1) |
式中,(x1, y1)表示待转换坐标;(x2, y2)表示转换后坐标;Δx0、Δy0表示坐标变换平移参数;m表示尺度比参数;α表示旋转角参数。
1.2 三维7参数转换模型不同坐标系由于椭球大小、定位和定向的差异,引起坐标的变化。对于空间三维直角坐标,一般旋转角较小,采用布尔沙7参数模型。
| $ \left[ {\begin{array}{*{20}{c}} {{X_2}}\\ {{Y_2}}\\ {{Z_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta {X_0}}\\ {\Delta {Y_0}}\\ {\Delta {Z_0}} \end{array}} \right] + \left( {1 + m} \right)\left[ {\begin{array}{*{20}{c}} 1&{{\varepsilon _Z}}&{ - {\varepsilon _Y}}\\ { - {\varepsilon _Z}}&1&{{\varepsilon _X}}\\ {{\varepsilon _Y}}&{ - {\varepsilon _X}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_1}}\\ {{Y_1}}\\ {{Z_1}} \end{array}} \right] $ | (2) |
式中,(X1, Y1, Z1)表示待转换坐标;(X2, Y2, Z2)表示转换后坐标;ΔX0、ΔY0、ΔZ0为3个平移参数;εX、εY、εZ为3个旋转参数;m为尺度变化参数。
1.3 格网改正量模型格网改正量模型的主要思想是:将转换区域划分为规则格网,根据区域内公共点坐标分量差值,采用一定的数学模型求取各格网点坐标分量差值,生成坐标差格网数据。进行坐标转换时,根据格网数据内插待转换点坐标改正量。格网模型的建立,可以采用相似变换法、多元回归法、最小曲率法等多种方法[6-11]。
2 ArcGIS对坐标转换的实现 2.1 空间校正工具ArcGIS中二维4参数法可以采用空间校正工具来实现,校正方法选择相似变换,按照“ < ID> < from_y> < from_x> < to_y> < to_x>”的格式准备控制点文本链接文件,并查看残差和均方根误差剔除误差较大点。在编辑状态下,选择需要转换的图层,进行校正。
2.2 创建自定义地理变换变换工具ArcGIS工具箱中包含了“创建自定义地理变换变换”工具,支持基于方程和基于格网两种坐标转换方法,同时也内置了部分转换参数和格网,但缺少现行参心坐标系与2000国家大地坐标系的转换参数。
基于方程方法可归纳为4参数法、7参数法、Molodensky法和简化Molodensky法。使用7参数法时,在创建自定义地理变换变换工具中,设置源坐标系和目标坐标系,变换方法选择COORDINATE_FRAME,输入计算的布尔沙7参数,建立这两个坐标系间的转换模型。当需要对数据进行坐标转换时,选择投影工具,地理变换会自动匹配可用的转换模型。
基于格网方法首先需要根据格网文件格式准备好格网文件,将制作好的格网文件放到ArcGIS安装目录的pedata文件夹的相应格式中,设置转换方法和格网文件名称,便可以创建gtf格式自定义坐标转换方法。基于格网方法的文件存储格式主要有NTv2方法和NADCON方法两种。NTv2文件格式:支持多级格网的高精度插值,同时还存储了每个点的精度,可存储为*.asc的ASCII文本形式,以及*.gsb的二进制形式。如图 1所示。NADCON文件格式:以十进制秒为单位,将格网点纬度差和经度差分别存放在两个文件中,存储为*.laa、*.loa的ASCII文本形式,以及*.las、*.loa的二进制形式。如图 2、图 3所示。
 |
| 图 1 NTv2格网存储格式 Fig.1 Storage Format of NTv2 Grid |
 |
| 图 2 NADCON格网Iaa存储格式 Fig.2 Laa Storage Format of NADCON Grid |
 |
| 图 3 NADCON格网loa存储格式 Fig.3 Loa Storage Format of NADCON Grid |
3 坐标转换精度分析 3.1 坐标转换参数精度分析
选取1°×1°实验区范围,共收集1980西安坐标系和2000国家大地坐标系重合点80个,提取其中69个点计算模型参数,剩余11个作为检核点。分别计算3种模型1980西安坐标系向2000国家大地坐标系转换的参数,并利用80个点的1980西安坐标系坐标制作ArcGIS shp点文件,采用建立的方法进行坐标转换,分析不同模型转换图形的精度。如图 4、图 5所示。
 |
| 图 4 3种模型计算参数点转换残差 Fig.4 Transformation Residuals of Calculate Parameter Points for Three Models |
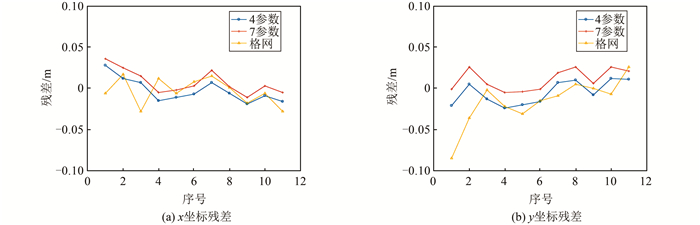 |
| 图 5 3种模型检核点转换残差 Fig.5 Transformation Residuals of Check Points for Three Models |
图 4和图 5反映了80个重合点的转换残差,可以看出转换残差主要分布在±5 cm范围内。对转换结果进行统计,如表 1和表 2所示,可以看出,标准差优于3 cm。
| 表 1 3种模型坐标转换内符合精度比较/m Tab.1 Comparison of Internal Accuracy for Three Models /m |
 |
| 表 2 3种模型坐标转换外符合精度比较 /m Tab.2 Comparison of External Accuracy for Three Models /m |
 |
3.2 数字线划图转换适用性和精度分析
为了验证数字线划图转换适用性,选取试验区范围内点、线、面三种要素类数据,利用建立的转换模型对其进行转换实验。限于篇幅,图 6显示了转换前局部图,图 7显示了格网法转换后结果。结果表明,转换精度、完整性、一致性均满足要求,从而进一步说明了基于ArcGIS参数法和格网法进行坐标转换的适用性。
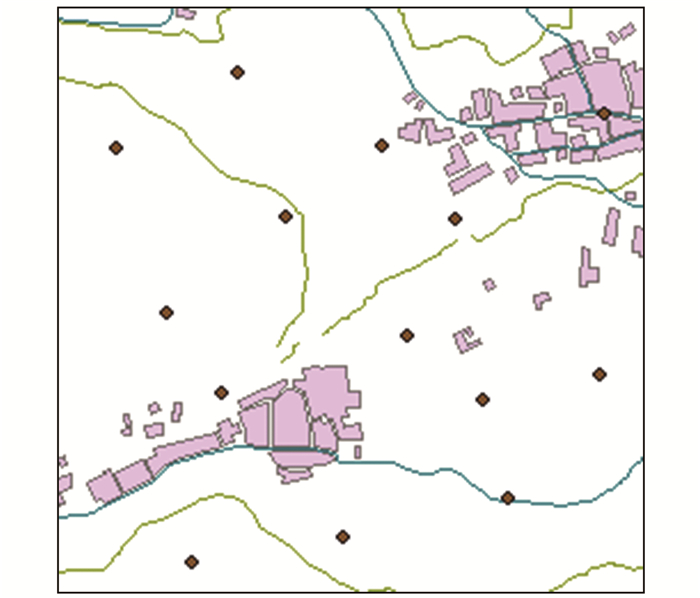 |
| 图 6 转换前局部图 Fig.6 Partial Map Before Transformation |
 |
| 图 7 转换前后叠加局部图 Fig.7 Overlay Partial Map Before and After Transformation |
4 结束语
通过实验数据转换分析,验证了ArcGIS对数字线划图坐标转换的实现,并对不同模型的转换精度进行了分析。结果表明,三种方法都能够满足ArcGIS图形转换精度要求。对于小区域可以选择4参数和7参数模型,而针对大范围情况,为避免分区接边,可以选择格网方法进行转换。本文分析了1980西安坐标系向2000国家大地坐标系适用性与精度,但方法同样适用于其他地方坐标系的转换工作。
| [1] |
张训虎, 刘晋虎, 何川, 等. 2000国家大地坐标系转换常见问题分析[J]. 测绘通报, 2016(9): 52-55. |
| [2] |
孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2010.
|
| [3] |
汤国安, 杨昕. ArcGIS地理信息系统空间分析实验教程[M]. 北京: 科学出版社, 2012.
|
| [4] |
蒋丽, 邹时林. CAD到GIS数据的属性匹配和转换的研究[J]. 测绘地理信息, 2017, 42(3): 58-62. |
| [5] |
李云岭, 薛雨, 贾沛哲, 等. 基于ArcGIS的大比例尺植物专题地图制作-以山东科技大学校园为例[J]. 测绘地理信息, 2018, 43(3): 55-58. |
| [6] |
Dewhurst W T. NADCON: the Application of Minimum-Curvature-Derived Surfaces in the Transformation of Position Data from the North American Datum of 1927 to the North American Datum of 1983[R]. NOAA Technical Memorandum, Rockville, 1999
|
| [7] |
Collier P. Development of Australia's National GDA94 Transformation Grids[C]. Consultant's Report to the Intergovernmental Committee on Surveying and Mapping, University of Melbourne, Australia, 2002
|
| [8] |
吕志平, 魏子卿, 李军, 等. CGCS2000高精度坐标转换格网模型的建立[J]. 测绘学报, 2013, 42(6): 791-797. |
| [9] |
袁修孝, 付迎春, 张过, 等. 多级空间信息网格间的平面坐标变换精度分析[J]. 武汉大学学报·信息科学版, 2005, 30(2): 110-114. |
| [10] |
郭充, 吕志平, 李岩, 等. 基于格网的坐标转换方法[J]. 信息工程大学学报, 2010, 11(2): 166-169. |
| [11] |
管真, 黄声享, 容金岩. 基于ArcGIS的地貌晕渲图制作实验分析[J]. 测绘地理信息, 2017, 42(2): 101-103. |
 2021, Vol. 46
2021, Vol. 46

