| 智能手机传感器标定的似线性模量方法 |
2. 中船勘察设计研究院有限公司,上海,200063
2. China Shipbuilding Industry Institute of the Engineering Investigation & Design Co., Ltd., Shanghai 200063, China
近年来,以智能手机为代表的智能移动客户端因其内置了微机电系统(micro electro mechanical systems, MEMS)而被广泛应用于与移动客户端相关的应用服务,如基于智能手机的室内地图导航、姿态识别、应急救援等[1-5]。但智能手机中的MEMS惯性传感器一般成本低、精度低且稳定性差,长时间应用也会严重影响测量精度。因此,对惯性传感器进行误差标定具有重要的应用价值。
目前,MEMS惯性传感器标定方法大多是基于九参数模型[6-9],并提出了多种误差标定的方法。现有方法可归纳为分量法和模量法两类。分量法也可称为直接解法,采用多位置标定数据,直接对误差模型中的各参数进行逐个求解或最小二乘整体求解,但需严格控制标定平台的位置或姿态[10-12]。现有模量法又可分为两步法和微分迭代法。其中,两步法是在误差模型基础上构建二次曲面模型,即椭球模型,以最小二乘法求解椭球模型参数,进而求解校正参数,计算过程繁杂[6, 13];而微分迭代法对椭球模型进行一阶泰勒展开,进而采用迭代方法求解,解算非常繁杂[14]。
本文详细探讨了九参数模型的6种形式,提出了一种适用于MEMS惯性传感器(加速度计、陀螺仪)的标定方法--似线性模量解法,其数据采集简便,迭代估计快速收敛,且无需严格的实验平台条件。基于实测的加速度计、陀螺仪数据对现有的分量解法与所提出的方法进行计算分析,结果验证了本文方法的正确性和有效性。
1 传感器标定方法 1.1 九参数模型对于传感器的误差标定,需根据其存在的误差特性进行误差模型的构建。传感器误差主要包括确定性误差和随机误差,其中确定性误差包括传感器各轴的零偏误差和标度因数误差,以及3轴间的非正交安装误差,随机误差包括不确定因素引起的随机误差,并受外界温度影响[15]。因此,文中仅对确定性误差在相对稳定常温条件下进行误差标定和校正参数估计,且忽略存在的二阶及以上动态小量误差。
对每个轴的零偏误差、标度因数误差以及3轴非正交误差进行标定,构成具有9个校正参数的传感器误差数学模型。现有文献介绍的九参数模型包括以下3种:
1) 模型1[4]。z轴与理论z轴重合,x轴与z轴间非正交系数θx z,y轴与x、z轴间非正交系数θy x、θy z。
2) 模型2[5]。z轴与理论z轴重合,y轴与z轴间非正交系数θy z,x轴与y、z轴间非正交系数θx y、θx z。
3) 模型3[6]。x轴与理论x轴重合,y轴与x轴间非正交系数θy x,z轴与x、y轴间非正交系数θz x、θz y。
分析以上3种模型可知,完备的九参数模型还应包括以下3种模型形式:
4) 模型4。x轴与理论x轴重合,z轴与x轴间非正交系数θz x,y轴与x、z轴间非正交系数θy x、θy z,模型为:
| $\begin{gathered} \left( \begin{gathered} {{\hat x}_{{\text{sensor}}}} \hfill \\ {{\hat y}_{{\text{sensor}}}} \hfill \\ {{\hat z}_{{\text{sensor}}}} \hfill \\ \end{gathered} \right) = \hfill \\ {\left[ {\begin{array}{*{20}{c}} {1 + {k_x}}&0&0 \\ {{\theta _{yx}}}&{1 + {k_y}}&{{\theta _{yz}}} \\ {{\theta _{zx}}}&0&{1 + {k_z}} \end{array}} \right]_{{\text{sensor}}}}\left( \begin{gathered} {x_{{\text{sensor}}}} \hfill \\ {y_{{\text{sensor}}}} \hfill \\ {z_{{\text{sensor}}}} \hfill \\ \end{gathered} \right) + {\left( \begin{gathered} {d_x} \hfill \\ {d_y} \hfill \\ {d_z} \hfill \\ \end{gathered} \right)_{{\text{sensor}}}} \hfill \\ \end{gathered} $ | (1) |
5) 模型5。y轴与理论y轴重合,x轴与y轴间非正交系数θx y,z轴与x、y轴间非正交系数θz x、θz y,模型为:
| $\begin{gathered} \left( \begin{gathered} {{\hat x}_{{\text{sensor}}}} \hfill \\ {{\hat y}_{{\text{sensor}}}} \hfill \\ {{\hat z}_{{\text{sensor}}}} \hfill \\ \end{gathered} \right) = \hfill \\ {\left[ {\begin{array}{*{20}{c}} {1 + {k_x}}&{{\theta _{xy}}}&0 \\ 0&{1 + {k_y}}&0 \\ {{\theta _{zx}}}&{{\theta _{zy}}}&{1 + {k_z}} \end{array}} \right]_{{\text{sensor}}}}\left( \begin{gathered} {x_{{\text{sensor}}}} \hfill \\ {y_{{\text{sensor}}}} \hfill \\ {z_{{\text{sensor}}}} \hfill \\ \end{gathered} \right) + {\left( \begin{gathered} {d_x} \hfill \\ {d_y} \hfill \\ {d_z} \hfill \\ \end{gathered} \right)_{{\text{sensor}}}} \hfill \\ \end{gathered} $ | (2) |
6) 模型6。y轴与理论y轴重合,z轴与y轴间非正交系数θz y,x轴与y、z轴间非正交系数θx y、θx z,模型为:
| $\begin{gathered} \left( \begin{gathered} {{\hat x}_{{\text{sensor}}}} \hfill \\ {{\hat y}_{{\text{sensor}}}} \hfill \\ {{\hat z}_{{\text{sensor}}}} \hfill \\ \end{gathered} \right) = \hfill \\ {\left[ {\begin{array}{*{20}{c}} {1 + {k_x}}&{{\theta _{xy}}}&{{\theta _{xz}}} \\ 0&{1 + {k_y}}&0 \\ 0&{{\theta _{zy}}}&{1 + {k_z}} \end{array}} \right]_{{\text{sensor}}}}\left( \begin{gathered} {x_{{\text{sensor}}}} \hfill \\ {y_{{\text{sensor}}}} \hfill \\ {z_{{\text{sensor}}}} \hfill \\ \end{gathered} \right) + {\left( \begin{gathered} {d_x} \hfill \\ {d_y} \hfill \\ {d_z} \hfill \\ \end{gathered} \right)_{{\text{sensor}}}} \hfill \\ \end{gathered} $ | (3) |
式(1)~式(3)中,sensor表示某传感器类型;xsensor、ysensor、zsensor表示传感器的3轴测量值;
将文献[4]中模型1的待求参数表示为向量形式,则可转化成矩阵形式为:
| $\begin{gathered} \left( \begin{gathered} {{\hat x}_{{\rm{sensor}}}} \hfill \\ {{\hat y}_{{\rm{sensor}}}} \hfill \\ {{\hat z}_{{\rm{sensor}}}} \hfill \\ \end{gathered} \right) = {\left[ {\begin{array}{*{20}{c}} x&0&0&1&0&0&z&0&0 \\ 0&y&0&0&1&0&0&x&z \\ 0&0&z&0&0&1&0&0&0 \end{array}} \right]_{{\rm{sensor}}}} \cdot \hfill \\ \mathit{\boldsymbol{\beta }} + \left( \begin{gathered} {x_{{\rm{sensor}}}} \hfill \\ {y_{{\rm{sensor}}}} \hfill \\ {z_{{\rm{sensor}}}} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} $ | (4) |
式中,β=[kx ky kz dx dy dz θyx θzx θzy]T。
当采集3个及以上标定位置的数据,便可利用式(4)列误差模型,以最小二乘方法拟合求解校正参数。该方法存在的不足是数据采集时需要专门的试验平台,对传感器标定位置或姿态进行严格控制,以获得传感器3轴分量的预设值;优点是该方法为线性模型,基于最小二乘便可进行求解,参数估计过程无需迭代。
同理,其他5种模型均可转化为与式(4)类似的矩阵形式,限于篇幅,不再赘述。
1.3 似线性模量法加速度计在静止或匀速运动状态下仅受地球重力场的影响,其3轴观测加速度矢量与当地重力矢量g相等;而陀螺仪的数据受地球自转的影响可忽略不计,将其置于单轴匀速转台时,陀螺仪3轴观测角速度向量的模不变,角速度ω与转台相等。因此,可认为传感器的校正值满足条件为:
| $\hat x_{{\text{sensor}}}^1 + \hat y_{{\text{sensor}}}^2 + \hat z_{{\text{sensor}}}^2 = \left\| R \right\|_{{\text{sensor}}}^2$ | (5) |
式中,‖·‖为矢量的2范数;R表示传感器理论值或实际值,当传感器为加速度计时,R为当地重力值;当传感器为陀螺仪时,R为转台速率值。
上述等式为非线性方程,一般采用一阶泰勒线性化进行迭代估计,该估计过程较为繁杂[7]。为此,本文将文献[4]中的模型1代入式(5),采用多项式分解的原理,将式(5)转化成矩阵形式为:
| $\left[ {{A_1}\;\;{A_2}\;\;{A_3}\;\;{A_4}\;\;{A_5}\;\;{A_6}\;\;{A_7}\;\;{A_8}\;\;{A_9}} \right] \cdot \mathit{\boldsymbol{\beta = }}L$ | (6) |
式中,设计矩阵和常数向量为:
| $\left\{ \begin{align} & {{A}_{1}}={{x}^{2}}\left( 2+{{k}_{x}} \right) \\ & {{A}_{2}}={{y}^{2}}\left( 2+{{k}_{y}} \right) \\ & {{A}_{3}}={{z}^{2}}\left( 2+{{k}_{z}} \right) \\ & {{A}_{4}}=2x\left( 1+{{k}_{x}} \right)+z{{\theta }_{xz}}+{{d}_{x}} \\ & {{A}_{5}}=2y\left( 1+{{k}_{y}} \right)+x{{\theta }_{yx}}+z{{\theta }_{yz}}+{{d}_{y}} \\ & {{A}_{6}}=2z\left( 1+{{k}_{z}} \right)+{{d}_{z}} \\ & {{A}_{7}}={{z}^{2}}{{\theta }_{xz}}+2xz\left( 1+{{k}_{x}} \right)+z{{d}_{x}} \\ & {{A}_{8}}={{x}^{2}}{{\theta }_{yx}}+2xy\left( 1+{{k}_{y}} \right)+xz{{\theta }_{yz}}+x{{d}_{y}} \\ & {{A}_{9}}={{z}^{2}}{{\theta }_{yz}}+2yz\left( 1+{{k}_{y}} \right)+xz{{\theta }_{yx}}+z{{d}_{y}} \\ & L={{R}^{2}}-{{x}^{2}}-{{y}^{2}}-{{z}^{2}} \\ \end{align} \right.$ | (7) |
分析式(6)可知,仅设计矩阵含有校正参数,其形式上与线性模型非常相似,故本文称为似线性模量法。当采集9个及以上标定位置的数据,便可利用式(6)、式(7)列误差模型,以最小二乘拟合求解校正参数。该方法的不足是其本质上为非线性方法,估计过程需要迭代处理(初始值设置为β(0)=0);其优点是不要求已知传感器3轴分量的预设值,因此,无需设计数据采集平台对传感器标定位置或姿态进行严格控制。此外,本文方法不需要对常数向量进行迭代更新,仅需要更新设计矩阵,因而较常规的一阶泰勒迭代方法简便快捷。
同理,其他5种模型均可代入式(5),经多项式分解可得到与式(6)相仿的似线性方程,限于篇幅,不再赘述。
2 智能手机实验结果与分析 2.1 标定实验方案为验证似线性模量法的正确性和有效性,采用该方法和现有分量法在室内常温情况下进行多个位置标定对比实验。实验以三星S3手机作为数据采集设备,利用Android语言开发的软件进行加速度和角速率数据采集(频率为50 Hz)。手机自然坐标系定义为:x轴为屏幕水平向右(正常手握手机),z轴为屏幕正面朝外,x、y、z符合右手系。实验过程中利用水准泡(4″)对数据采集设备进行整平,以满足现有分量法对采集设备姿态控制的要求。
为提高校正参数的估计精度,采集方案均设计3个多余标定位置。对于分量法,采用6个非倾斜姿态标定位置进行标定;对于似线性模量法,采用12个标定位置进行标定,包含6个非倾斜姿态和6个倾斜姿态标定位置。数据采集方案如下。
1) 加速度数据采集。对于非倾斜姿态,智能手机水平放置于静止平台上(当地重力加速度值为9.796 7 m/s2),如图 1所示,依次调整6个标定位置,利用水准气泡精确整平并采集加速度数据。对于倾斜姿态,智能手机按一定倾角放置于平台上,6个标定位置如图 2所示,依次将x、y、z轴中的一轴置于水平面内,另两轴平面与竖直方向夹角约为45°。
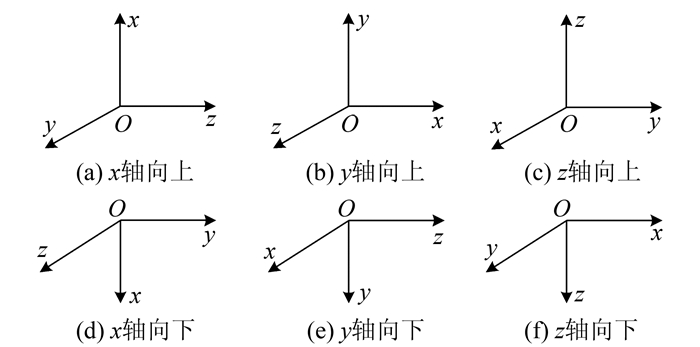 |
| 图 1 非倾斜姿态示意图 Figure 1 Diagram of Non-Tilted Attitude |
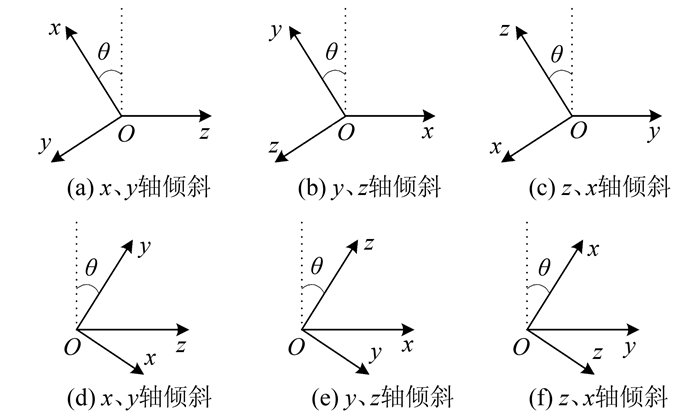 |
| 图 2 倾斜姿态示意图 Figure 2 Diagram of Tilted Attitude |
2) 陀螺仪角速率数据采集。智能手机放置于匀速单轴转台上(角速率为0.751 4 rad/s),与加速度数据采集方式相同,分别按图 1、图 2采集非倾斜姿态和倾斜姿态数据,采集时间均为3 min。
2.2 计算结果及分析对于不同的惯性传感器,在前文介绍的6种九参数模型中,存在一种最适用的模型。为检验各种模型的适用性,分别利用分量法和似线性模量法对各个模型进行校正参数计算。标定参数结果表明,模型1适用于三星S3手机加速度传感器校正,模型5适用于三星S3手机陀螺仪传感器校正。为节省篇幅,仅列出了基于模型1的加速度计校正参数和基于模型5的陀螺仪校正参数,如表 1所示。
| 表 1 两种方法的校正参数对比 Table 1 Calibration Parameters of Accelerometer and Gyroscope with Two Methods |
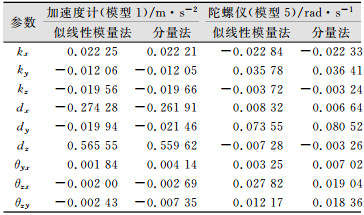 |
由表 1可知,加速度计和陀螺仪经过似线性模量法和分量法标定后,得到的相对应的校正参数值基本相等,验证了似线性模量法的正确性。为进一步验证似线性模量法的有效性,选取6个静态非倾斜位置的两类传感器数据,分别将分量法和似线性模量法求解的校正参数代入模型中,对加速度计、陀螺仪的数据分别进行校正,并与各对应位置数据的预设值作差求取残差,计算传感器经两种方法校正后的残差。加速度计x轴经两种方法校正后的残差对比结果如图 3所示,陀螺仪x轴经两种方法校正后的残差如图 4所示,传感器两种方法的残差中误差统计如表 2所示。
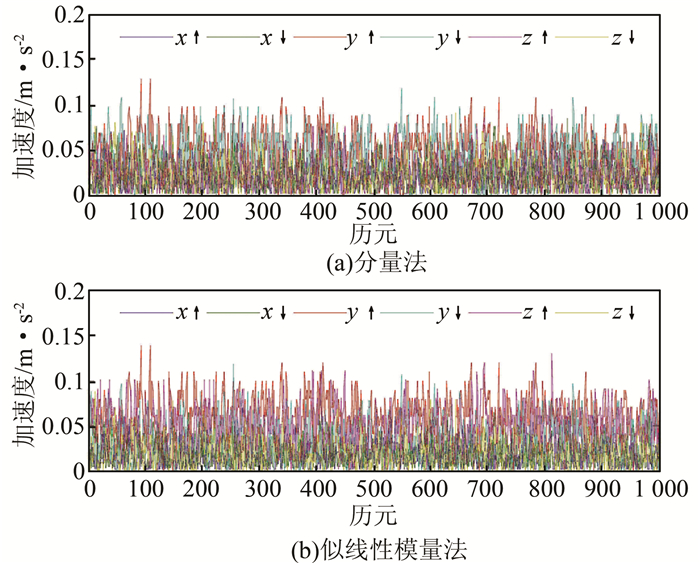 |
| 图 3 加速度计x轴误差校正的残差 Figure 3 Residual of Accelerometer x-Axis After Error Correction |
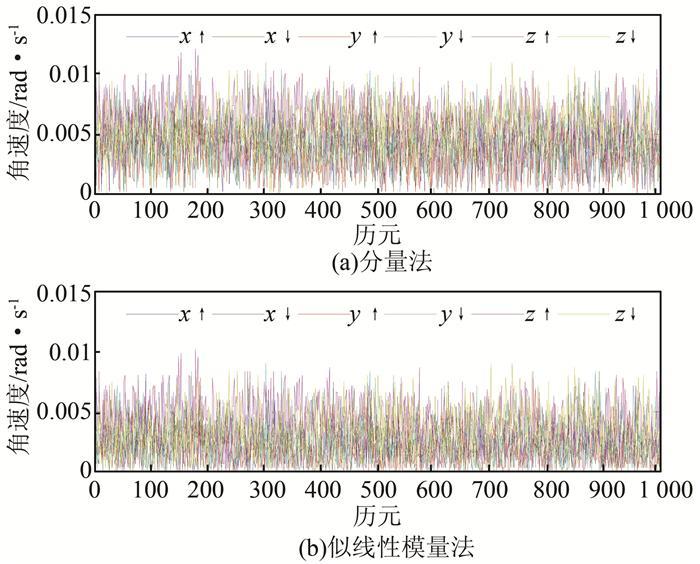 |
| 图 4 陀螺仪x轴误差校正的残差 Figure 4 Residual of Gyroscope x-Axis After Error Correction |
| 表 2 两种方法误差校正的残差中误差 Table 2 Residual RMSE of Two Methods After Error Correction |
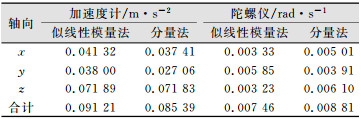 |
比较图 3(a)与图 3(b)可知,6个静态非倾斜位置的x轴加速度数据经过分量法、似线性模量法分别标定后,其残差的绝对值均在(0, 0.1) m/s2范围内,且分量法略优于似线性模量法。比较图 4(a)与图 4(b)可知,6个静态非倾斜位置的x轴角速率数据经过分量法、似线性模量法分别标定后,其残差值的绝对值均处于(0, 0.01) rad/s范围内,似线性模量法要优于分量法。进一步分析表 2可知,对于加速度计3轴标定中误差,分量法总体略优于似线性模量法;对于陀螺仪3轴标定中误差,似线性模量法总体略优于分量法。由此可知,本文所提方法与分量法的标定精度相当,同时验证了本文所提方法的正确性和有效性。
3 结束语本文对现有传感器误差标定方法的优缺点进行了总结与分析,给出了九参数模型的6种完备形式,并在此基础上提出了一种传感器误差标定的似线性模量解法。该方法在椭球模型基础上进行多项式分解,得到一种简便的似线性化迭代模型,且校正精度与分量法相当。需指出的是,似线性模量解法本质仍为非线性模型,需给定参数初值迭代求解。该方法的优点是,不要求已知传感器3轴分量的预设值,迭代估计快速收敛(迭代初始值取0时,一般5次即可收敛),且标定过程中无需严格控制平台姿态或位置,数据采集过程高效简便。
| [1] |
徐元坤. 基于Wi-Fi和Android平台的室内定位技术研究[J].
测绘地理信息,2014,39(5) : 21–24.
Xu Yuankun. Indoor Location Based on Wi-Fi and Android Platform[J]. Journal of Geomatics,2014,39(5) : 21–24. |
| [2] |
李景辉, 杨立才. 基于多传感器信息融合的人体姿态解算算法[J].
山东大学学报(工学版),2013,43(5) : 49–54.
Li Jinghui, Yang Licai. An Attitude Estimation Algorithm for Human Body Based on Multi-Sensor Information Fusion[J]. Journal of Shandong University (Engineering Science),2013,43(5) : 49–54. |
| [3] |
王海鹏, 王正良, 许威威, 等. 基于三维模型的Android手机端人脸姿态实时估计系统[J].
计算机应用,2015,35(8) : 2321–2326.
Wang Haipeng, Wang Zhengliang, Xu Weiwei, et al. Real-Time Face Pose Estimation System Based on 3D Face Model on Android Mobile Platform[J]. Journal of Computer Applications,2015,35(8) : 2321–2326. |
| [4] | Yang L, Dashti M, Jie Z. Indoor Localization on Mobile Phone Platforms Using Embedded Inertial Sensors[C]. The 10th Workshop on Positioning, Navigation and Communication, IEEE, Dresden, Germany, 2013 |
| [5] | Placer M, Kova S. Enhancing Indoor Inertial Pedestrian Navigation Using a Shoe-Worn Marker[J]. Sensors,2013,13(8) : 9836–9859. DOI:10.3390/s130809836 |
| [6] |
龙达峰, 刘俊, 张晓明, 等. 基于椭球拟合的三轴陀螺仪快速标定方法[J].
仪器仪表学报,2013,34(6) : 1299–1305.
Long Dafeng, Liu Jun, Zhang Xiaoming, et al. Triaxial Gyroscope Fast Calibration Method Based on Ellipsoid Fitting[J]. Chinese Journal of Scientific Instrument,2013,34(6) : 1299–1305. |
| [7] | Dorveaux E, Vissiere D, Martin A P, et al. Iterative Calibration Method for Inertial and Magnetic Sensors[C]. IEEE Conference on Decision & Control, Shanghai, 2009 http://www.oalib.com/references/17028163 |
| [8] | Artese G, Trecroci A. Calibration of a Low Cost MEMSINS Sensor for an Integrated Navigation System[C]. The 21st ISPRS, Beijing, 2008 |
| [9] |
任建新, 杜亚宁, 杨星辉, 等. 实用的MEMS惯性器件外场标定方法[J].
传感器与微系统,2014,33(6) : 27–30.
Ren Jianxin, Du Yaning, Yang Xinghui, et al. Outfield Calibration Method for Practical MEMS Inertial Device[J]. Transducer and Microsystem Technologies,2014,33(6) : 27–30. |
| [10] |
宋丽君, 秦永元. 微机电加速度计的六位置标定[J].
传感技术学报,2009,22(11) : 1557–1561.
Song Lijun, Qin Yongyuan. Six-Position Testing of MEMS Accelerometer[J]. Chinese Journal of Sensors and Actuators,2009,22(11) : 1557–1561. |
| [11] |
李巍, 任顺清, 赵洪波. 三轴转台误差对陀螺仪标定精确度的影响[J].
电机与控制学报,2011,15(10) : 101–106.
Li Wei, Ren Shunqing, Zhao Hongbo. Influence of Three-Axis Turntable Error on Gyro Calibration Accuracy[J]. Electric Machines and Control,2011,15(10) : 101–106. |
| [12] |
乌伟, 赵严, 宁永权, 等. 微惯性测量单元的标定技术研究[J].
电光与控制,2013,20(8) : 54–57.
Wu Wei, Zhao Yan, Ning Yongquan, et al. On Calibration of Micro Inertial Measurement Unit[J]. Electronics Optics & Control,2013,20(8) : 54–57. |
| [13] | Foster C C, Elkaim G H. Extension of a Two-Step Calibration Methodology to Include Nonorthogonal Sensor Axes[J]. Aerospace and Electronic Systems, IEEE Transactions on,2008,44(3) : 1070–1078. DOI:10.1109/TAES.2008.4655364 |
| [14] |
范玉宝, 李杰, 张晓明, 等. 基于椭球拟合的微惯性测量组合现场快速标定方法[J].
传感技术学报,2011,24(11) : 1547–1550.
Fan Yubao, Li Jie, Zhang Xiaoming, et al. A Rapid Field Calibrating Method for Micro Inertial Measurement Unit Based on Ellipsoid Fitting[J]. Chinese Journal of Sensors and Actuators,2011,24(11) : 1547–1550. |
| [15] |
王化会, 袁冬莉. MEMS惯性测量单元的精确定标技术[J].
计算机测量与控制,2011,19(6) : 1315–1317.
Wang Huahui, Yuan Dongli. A Precision-Calibration Technique for Inertial Measurement Units Based on MEMS[J]. Computer Measurement & Control,2011,19(6) : 1315–1317. |
 2016, Vol. 41
2016, Vol. 41


