| 几何精度衰减因子对两种到达时间差算法定位精度的影响分析 |
GDOP最早应用于GPS定位中,文献[1]将其定义为“几何精度衰减因子”,即传感器相对于待测点的几何布局对定位精度衰减作用的量化表达。在定位算法和提高定位精度的研究中,分析GDOP对定位结果的影响及其重要。国内外学者对GDOP进行了大量研究。Chaffee等[2]分析了基于到达时间(time of arrival,TOA)的伪距定位中GDOP与定位精度理论下界CRLB(Cramér-Rao lower bound)的关系;Yarlagadda等[3]研究了多颗卫星GDOP的最小值和单颗卫星的GDOP贡献值,并给出了单颗卫星贡献值的计算表达式; 丛丽等[4]分析了坐标系变换对GDOP的改变以及不同卫星加权GDOP对定位精度的影响;盛琥等[5]修正了文献[3]的GDOP最小值;Tseng等[6]提出了GDOP协助定位方法,通过设立虚拟基站提高定位精度。
随着定位技术的发展,定位关注热点逐渐从室外走向室内。基于到达时间差(time difference of arrival,TDOA)的定位方法是室内定位中一种经典的测距定位方法,其通过测量待测点到不同已知传感器点的到达时间差得到测距值,然后利用双曲线模型估计待测点坐标[7],在电磁波视距传输(light of sight,LOS)情况下具有较高精度,并且与指纹定位相比工作量较小[8]。常见的基于TDOA的定位算法有Taylor算法、Chan算法及相关衍生算法。Taylor算法通过泰勒公式将观测方程线性化后舍去高次项,然后采用局部最小二乘准则进行迭代求解,在初始值接近真值的情况下获得较高的定位精度[9]。Chan等[10]提出了一种不需要指定初始值的两步定位算法,简称Chan算法。仿真表明,在测距误差较小时,Chan算法与Taylor算法的定位精度相当,理论上可以达到精度下界CRLB。
然而,文献[10]中对两种算法定位精度以及CRLB的比较仅限于几种特定情景,尤其没有考虑到不同GDOP值对定位精度的影响。实际上,两种经典算法依赖的数学模型都在舍去误差高次项时产生了截断误差。当传感器与待测点之间的几何布局变差,即GDOP值逐渐增大时,截断误差对定位精度的影响会被逐渐放大,甚至导致结果发散。不同数学模型的截断误差不同,相应的定位精度对GDOP值的敏感程度也有差异。因此,本文从GDOP的角度出发,通过理论推导和仿真分析,揭示了不同GDOP值下Chan算法与Taylor算法的定位精度差异,并阐述了两种算法定位精度与CRLB的接近程度。
1 GDOP与算法定位精度的关系设传感器数目为n,假设待测点到各个传感器的测距值r={r1, r2, …, rn}相互独立,并且所有测距值的误差服从同一N(0, σ2)分布。则TDOA观测值为:
| $ r_{i, 1}=r_{i}-r_{1}=\tilde{r}_{i, 1}-\varepsilon_{i, 1}, i=2, 3, \cdots, n $ | (1) |
式中,误差向量ε=[ε2, 1, ε3, 1, …, εn, 1]服从N(0, D)分布。由于ri, 1(i=2, 3, …, n)均含有r1,因此相互不独立。方差阵D的对角线元素为2σ2,非对角元素为σ2。令σ为单位权中误差,则协因数阵Q
| $ \boldsymbol{P}=\boldsymbol{Q}^{-1}=\left[\begin{array}{cccc} \frac{n-1}{n} & -\frac{1}{n} & \cdots & -\frac{1}{n} \\ -\frac{1}{n} & \frac{n-1}{n} & \cdots & -\frac{1}{n} \\ \vdots & \ddots & \ddots & \vdots \\ -\frac{1}{n} & -\frac{1}{n} & \cdots & \frac{n-1}{n} \end{array}\right]_{(n-1) \times(n-1)} $ | (2) |
下面分别推导GDOP与两种算法定位精度的关系。
1.1 Taylor算法TDOA观测方程可以表达为:
| $ \begin{array}{c} r_{i, 1}=r_{i}-r_{1}= \\ \sqrt{\left(x_{i}-x\right)^{2}+\left(y_{i}-y\right)^{2}+\left(z_{i}-z\right)^{2}} \\ \sqrt{\left(x_{1}-x\right)^{2}+\left(y_{1}-y\right)^{2}+\left(z_{1}-z\right)^{2}} \\ i=2, 3, \cdots, n \end{array}, $ | (3) |
式中,(x, y, z)为待测点坐标;(xi, yi, zi)为已知传感器坐标。
将式(3)从真值点处(
| $ \begin{array}{c} r_{i, 1}=\tilde{r}_{i, 1}-\left[e_{x, i}-e_{x, 1}, e_{y, i}-e_{y, 1}, e_{z, i}-e_{z, 1}\right] \Delta \theta \\ i=2, 3, \cdots, n \end{array} $ | (4) |
式中,
整理式(4)得到:
| $ \Delta r=\boldsymbol{B} \Delta \theta $ | (5) |
式中,
经过加权最小二乘法计算,可以得到:
| $ \Delta \theta=\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{P} \Delta r, \boldsymbol{D}_{\Delta \theta}=\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{B}\right)^{-1} \times \sigma^{2} $ | (6) |
式中,
因此,GDOP矩阵为(BTPB)-1, GDOP值为矩阵迹的平方根
Chan算法是一种不需要初始值的两步估计定位算法。由待测点到传感器的距离方程可得:
| $ \begin{array}{c} r_{i}^{2}=\left(x_{i}-x\right)^{2}+\left(y_{i}-y\right)^{2}+\left(z_{i}-z\right)^{2}= \\ K_{i}-2 x_{i} x-2 y_{i} y-2 z_{i} z+x^{2}+y^{2}+z^{2} \\ i=1, 2, 3, \cdots, n \end{array} $ | (7) |
式中,
| $ \begin{aligned} r_{i, 1}^{2}-K_{i}+K_{1}=-2 &\left(x_{i, 1} x+y_{i, 1} y+z_{i, 1} z+r_{i, 1} r_{1}\right), \\ & i=2, 3, \cdots, n \end{aligned} $ | (8) |
即得:
| $ \boldsymbol{h}_{1}=\boldsymbol{G}_{1} \boldsymbol{\theta}_{1} $ | (9) |
式中,
由式(9)可得误差向量ψ1:
| $ \boldsymbol{\psi}_{1}=\boldsymbol{h}_{1}-\boldsymbol{G}_{1} \tilde{\boldsymbol{\theta}}_{1}=\boldsymbol{B}_{1} \varepsilon+0.5 \varepsilon \odot \varepsilon $ | (10) |
式中,
舍去式(10)中的误差高次项,可以得到:
| $ \begin{aligned} \boldsymbol{D}_{1} &=E\left[\boldsymbol{\psi}_{1} \boldsymbol{\psi}_{1}^{\mathrm{T}}\right]=\boldsymbol{B}_{1} \boldsymbol{D} \boldsymbol{B}_{1} \\ \boldsymbol{P}_{1} &=\left(\frac{1}{\sigma^{2}} \boldsymbol{D}_{1}\right)^{-1}=\boldsymbol{B}_{1}^{-1} \boldsymbol{P} \boldsymbol{B}_{1}^{-1} \end{aligned} $ | (11) |
式中,D1为误差向量ψ1的方差阵;P1为第一步估计的权阵。
第一步估计考虑未知参数之间相互独立,采用加权最小二乘准则求解得到一步估值θ1:
| $ \begin{array}{c} \boldsymbol{\theta}_{1}=\left(\boldsymbol{G}_{1}^{\mathrm{T}} \boldsymbol{P}_{1} \boldsymbol{G}_{1}\right)^{-1} \boldsymbol{G}_{1}^{\mathrm{T}} \boldsymbol{P}_{1} \boldsymbol{h}_{1} \\ \boldsymbol{D}_{\boldsymbol{\theta}_{1}}=\left(\boldsymbol{G}_{1}^{\mathrm{T}} \boldsymbol{D}_{1}^{-1} \boldsymbol{G}_{1}\right)^{-1} \end{array} $ | (12) |
式中,Dθ1为θ1的估计精度。
由式(7)可知,第一步估计中未知参数(x, y, z)和r1实际上并不相互独立。因此建立第二步估计方程:
| $ \boldsymbol{h}_{2}=\boldsymbol{G}_{2} \boldsymbol{\theta}_{2} $ | (13) |
其中,
用第一步估值θ1代替h2中的真值,仿照第一步估计推导可得:
| $ \begin{array}{c} \boldsymbol{\psi}_{2}=\boldsymbol{h}_{2}-\boldsymbol{G}_{2} \tilde{\boldsymbol{\theta}}_{2}=2 \boldsymbol{B}_{2} \varepsilon_{1}+\varepsilon_{1} \odot {\varepsilon_{1}} \approx 2 \boldsymbol{B}_{2} \varepsilon_{1} \\ \boldsymbol{D}_{2}=E\left[\boldsymbol{\psi}_{2} \boldsymbol{\psi}_{2}^{\mathrm{T}}\right]=4 \boldsymbol{B}_{2} \boldsymbol{D}_{1} \boldsymbol{B}_{2} \\ \boldsymbol{P}_{2}=\left(\frac{1}{\sigma^{2}} \boldsymbol{D}_{2}\right)^{-1}=\frac{1}{4} \boldsymbol{B}_{2}^{-1} \boldsymbol{P}_{1} \boldsymbol{B}_{2}^{-1} \end{array} $ | (14) |
式中,ψ2为第二步估计的误差向量;D2为误差ψ2的方差阵;P2为第二步估计的权阵;θ1为第一步估值θ1的误差,
采用加权最小二乘准则求解得到两步估值θ2:
| $ \boldsymbol{\theta}_{2}=\left(\boldsymbol{G}_{2}^{\mathrm{T}} \boldsymbol{P}_{2} \boldsymbol{G}_{2}\right)^{-1} \boldsymbol{G}_{2}^{\mathrm{T}} \boldsymbol{P}_{2} \boldsymbol{h}_{2} $ | (15) |
对θ2开根号可以得到两个解,经过判断取舍与[x1 y1 z1]T相加即得到最终估值。最终的点位坐标估值精度表达式为:
| $ \boldsymbol{D}_{\theta}=\left(\boldsymbol{B}_{3} \boldsymbol{G}_{2}^{\mathrm{T}} \boldsymbol{B}_{2}^{-1} \boldsymbol{G}_{1}^{\mathrm{T}} \boldsymbol{B}_{1}^{-1} \boldsymbol{P} \boldsymbol{B}_{1}^{-1} \boldsymbol{G}_{1} \boldsymbol{B}_{2}^{-1} \boldsymbol{G}_{2} \boldsymbol{B}_{3}\right)^{-1} \times \sigma^{2} $ | (16) |
式中,
记B′=B1-1G1B2-1G2B3,由于B1、B2、B3是对角矩阵,所以式(16)等价于:
| $ \boldsymbol{D}_{\theta}=\left(\boldsymbol{B}^{\prime \mathrm{T}} \boldsymbol{P} \boldsymbol{B}^{\prime}\right)^{-1} \times \sigma^{2} $ | (17) |
理论坐标精度计算时用真值代替方程中的观测值,得到:
| $ \begin{array}{ccc} \boldsymbol{B}_{2}^{-1} \boldsymbol{G}_{2} \boldsymbol{B}_{3}=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ e_{x, 1} & e_{y, 1} & e_{z, 1} \end{array}\right] \boldsymbol{B}_{1}^{-1} \boldsymbol{G}_{1}=\\ -\left[\begin{array}{cccc} \frac{x_{2, 1}}{\tilde{r}_{2}} & \frac{y_{2, 1}}{\tilde{r}_{2}} & \frac{z_{2, 1}}{\tilde{r}_{2}} & \frac{\tilde{r}_{2, 1}}{\tilde{r}_{2}} \\ \frac{x_{3, 1}}{\tilde{r}_{3}} & \frac{y_{3, 1}}{\tilde{r}_{3}} & \frac{z_{3, 1}}{\tilde{r}_{3}} & \frac{\tilde{r}_{3, 1}}{\tilde{r}_{3}} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{x_{n, 1}}{\tilde{r}_{n}} & \frac{y_{n, 1}}{\tilde{r}_{n}} & \frac{z_{n, 1}}{\tilde{r}_{n}} & \frac{\tilde{r}_{n, 1}}{\widetilde{r}_{n}} \end{array}\right]\\ \boldsymbol{B}^{\prime}=\boldsymbol{B}_{1}^{-1} \boldsymbol{G}_{1} \boldsymbol{B}_{2}^{-1} \boldsymbol{G}_{2} \boldsymbol{B}_{3}= \\ {\left[\begin{array}{ccc} e_{x, 2}-e_{x, 1} & e_{y, 2}-e_{y, 1} & e_{z, 2} -e_{z, 1} \\ e_{x, 3}-e_{x, 1} & e_{y, 3}-e_{y, 1} & e_{z, 3} -e_{z, 1} \\ \vdots & \vdots & \vdots \\ e_{x, n}-e_{x, 1} & e_{y, n}-e_{y, 1} & e_{z, n}-e_{z, 1} \end{array}\right]=\boldsymbol{B}} \end{array} $ | (18) |
因此,DΔθ=Dθ,即理论上同一GDOP值对两种算法定位精度的衰减影响相同。
CRLB是无偏估计量的方差理论下界[11],文献[10]指出理论上Chan算法的定位精度能够达到CRLB。由以上推导可知Taylor算法的理论定位精度同样也可以达到。然而,在实际计算过程中,Taylor算法初值未知,且高次项忽略可能导致发散现象;Chan算法在推导过程中多次舍去误差二次项,并且用近似值代替真值。因此,通过仿真对比分析两种算法的实际定位精度和理论下界CRLB是有必要的。
2 仿真分析 2.1 随机场景仿真设测距误差独立且N(0, σ2)分布,由于两种方法的定位结果均在噪声小时不容易发散,仿真时测距误差标准差σ设为0.1 m。通常情况下GDOP最小值与传感器数量的平方根
| $ \operatorname{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^{10000}\left[\left(x_{i}-\tilde{x}\right)^{2}+\left(y_{i}-\tilde{y}\right)^{2}+\left(z_{i}-z\right)^{2}\right]}{10000}} $ | (19) |
仿真过程中,GDOP值大于10的样本数目很小,不便于统计分析,因此将GDOP阈值设为10。通过Matlab计算结果提示,去掉两次Taylor算法发散结果,仿真结果如图 1所示。
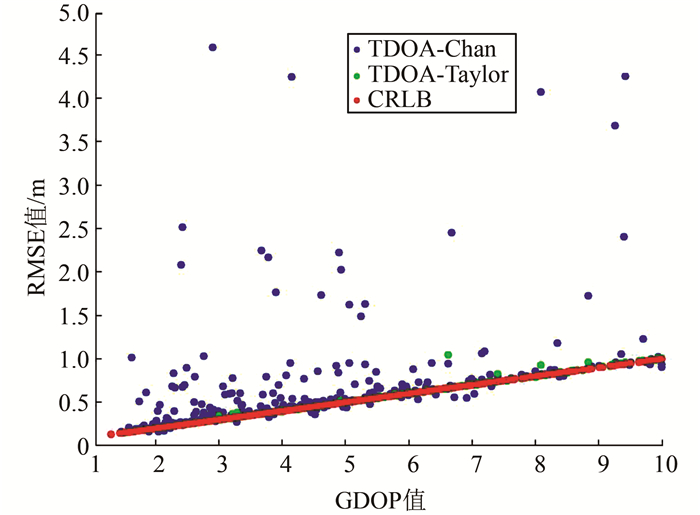 |
| 图 1 不同GDOP下两种算法定位精度与CRLB的比较 Fig.1 Comparison of Positioning Accuracy of Two Algorithms and CRLB in Different GDOP |
从图 1可以看出,在GDOP值1.5~10范围内,Taylor算法的实际定位精度基本上达到CRLB,并且几乎没有波动;而Chan算法的实际定位精度则稍差于CRLB,并且容易出现波动,RMSE最大差距可达到4 m。仿真结果显示其主要原因是在Chan算法考虑未知参数相关性的第二步估计时式(15)中求逆矩阵的条件数太大。
2.2 特定场景下仿真仿真类似地下车库场景的室内定位,场景范围为100 m×50 m×10 m,传感器数量n设为6,除传感器布局和待测点坐标外其他参数与§2.1相同。当传感器均布设在顶面上时,传感器共面会导致Chan算法的系数矩阵G1秩亏。因此,调整其中一个传感器的z坐标,将传感器坐标设置为:(0, 0, 10)m、(50, 0, 10)m、(100, 0, 10)m、(0, 50, 8)m,(50, 50, 10)m、(100, 50, 10)m。此时地面点的GDOP值分布如图 2所示。
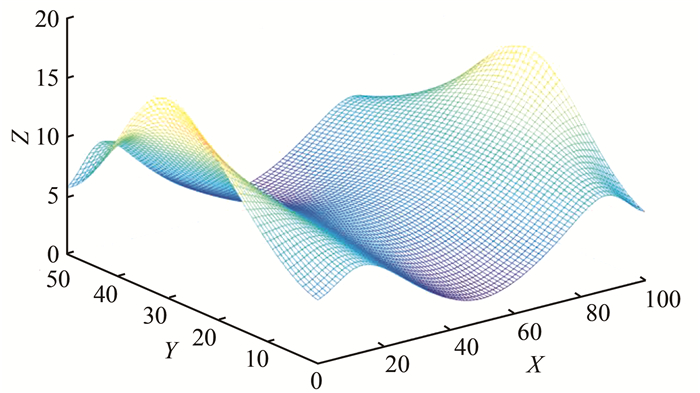 |
| 图 2 地面点GDOP值分布 Fig.2 GDOP Value Distribution of Ground Points |
从图 2可以看出,待测点从地面中心点沿X轴平行线向两边移动时,GDOP值逐渐增大。因此,以步长2 m从中心点按此线路依次采集26个样本点的GDOP值,并计算每一个样本点的定位精度RMSE。仿真得到两种算法的实际定位精度与CRLB的对比如图 3所示。Chan算法的实际定位精度和CRLB的差值与GDOP值的关系如图 4所示。
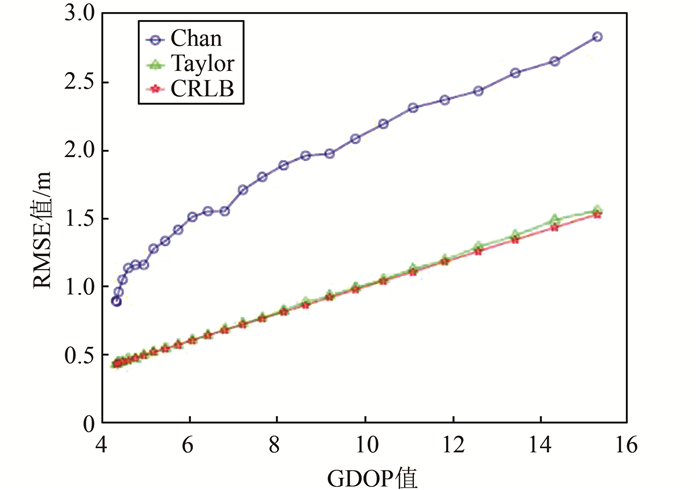 |
| 图 3 GDOP值与两种算法定位精度的关系 Fig.3 Relationship Between GDOP Value and Positioning Accuracy of Two Algorithms |
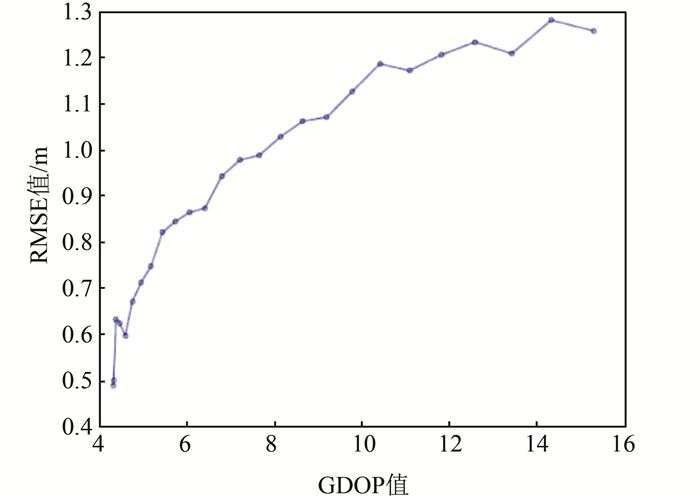 |
| 图 4 GDOP值与Chan-CRLB精度差值的关系 Fig.4 Relationship Between GDOP Value and Positioning Accuracy Difference of Chan and CRLB |
从图 3可以看出,在GDOP值4~15的范围内,Taylor算法的实际定位精度RMSE接近CRLB,Chan算法的实际定位精度RMSE无法达到理论最小值CRLB,最小差距为0.4 m。从图 4可以看出,随着GDOP值的增大(传感器几何布局变差),Chan算法的实际定位精度逐渐偏离CRLB,即Chan算法的实际定位精度和CRLB的差值与GDOP值基本呈正相关。
考虑到Chan算法的实际定位精度不如Taylor算法,但是用Chan算法可以为Taylor展开提供初值并使其收敛,而Taylor算法可以提高Chan算法在较差几何布局下的定位精度。因此,将Chan算法与Taylor算法结合进行仿真(简称Chan-Taylor混合算法),仿真设置与上面相同,结果如图 5所示。
 |
| 图 5 GDOP值与Chan-Taylor混合算法定位精度的关系 Fig.5 Relationship Between GDOP Value and Positioning Accuracy of Chan-Taylor Hybrid Algorithm |
从图 5可以看出,在GDOP值4~15范围内Chan-Taylor混合算法的实际定位精度与CRLB的最大差值小于0.1 m,远高于Chan算法的实际定位精度。因此,在增加计算量的前提下,Taylor算法改善了Chan算法的实际定位精度,使其接近CRLB;同时,Chan算法也为Taylor算法提供了初始值。所以,在计算资源足够的情况下,建议选择Chan-Taylor结合算法来改善定位精度。
3 结束语本文从GDOP的角度考虑,将基于TDOA的Taylor算法和Chan算法的实际定位精度与理论下界CRLB进行了对比分析。理论上,两者定位精度受GDOP的影响相同并且可以达到CRLB。实际上,算法中数学模型存在截断误差,两种算法的实际定位精度受GDOP值的影响存在差异。仿真结果显示,在随机GDOP值(几何布局)下Chan算法的实际定位精度容易波动,并且稍大于CRLB;Taylor算法的实际定位精度稳定且接近CRLB。在特定传感器布局下,Taylor算法的实际定位精度高于Chan算法,可以达到CRLB;Chan算法的实际定位精度无法达到CRLB,并且和CRLB的差值与GDOP值呈正相关。选择Chan算法与Taylor算法的结合进行定位,可以有效改善Chan算法的这一劣势。
室内定位完好性体系与传感器几何布局密切相关,优化几何布局在提高定位精度的同时也改善了定位系统的完好性指标。因此,通过GDOP和室内定位算法定位精度的关系来分析室内定位完好性风险指标将是下一步研究方向。
| [1] |
Kaplan E D, Hegarty C. Understanding GPS: Principles and Applications[M]. London: Artech House, 2005.
|
| [2] |
Chaffee J, Abel J.GDOP and the Cramer-Rao Bound[C]. Proceedings of 1994 IEEE Position, Location and Navigation Symposium, Las Vegas, NV, USA, 1994
|
| [3] |
Yarlagadda R, Ali I, Al-Dhahir N, et al. GPS GDOP Metric[J]. IEE Proceedings-Radar, Sonar and Navigation, 2000, 147(5): 259-264. |
| [4] |
丛丽, Abidat A I, 谈展中. 卫星导航几何因子的分析和仿真[J]. 电子学报, 2006, 34(12): 2204-2208. |
| [5] |
盛琥, 杨景曙, 曾芳玲. 伪距定位中的GDOP最小值[J]. 火力与指挥控制, 2009, 34(5): 22-24. |
| [6] |
Tseng P H, Feng K T. Geometry-Assisted Localization Algorithms for Wireless Networks[J]. IEEE Transactions on Mobile Computing, 2013, 12(4): 774-789. |
| [7] |
Mautz R.Indoor Positioning Technologies[D]. Zurich: Südwestdeutscher Verlag für Hochschulschriften, 2012
|
| [8] |
阮陵, 张翎, 许越, 等. 室内定位:分类、方法与应用综述[J]. 地理信息世界, 2015, 22(2): 8-14. |
| [9] |
赖琴.多径环境下的TDOA定位算法研究[D].武汉: 华中科技大学, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10487-1015906197.htm
|
| [10] |
Chan Y T, Ho K C. A Simple and Efficient Estimator for Hyperbolic Location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905-1915. |
| [11] |
齐民友. 概率论与数理统计[M]. 第2版. 北京: 高等教育出版社, 2011.
|
| [12] |
Levanon N. Lowest GDOP in 2-D Scenarios[J]. IET Radar, Sonar & Navigation, 2000, 147(2): 149-155. |
 2020, Vol. 45
2020, Vol. 45

