| 国产高分三号卫星干涉测量试验 |
合成孔径雷达(synthetic aperture radar,SAR)是一种利用图像处理技术合成大型虚拟天线的先进雷达系统,其空间分辨率远远高于实际孔径雷达。作为一种主动式微波传感器,SAR系统主动发射和接收目标区域回波散射的信号,且长波雷达信号大多不受天气或云层的影响。因此SAR能在大多数天气条件下有效工作,并能实现全天时、全天候对地观测,甚至可以透过地表或植被获取其掩盖的信息。因此,其逐渐成为地球空间信息获取的一种先进的技术手段,被广泛应用于测绘、海洋、城市环境监测、土地利用、军事等领域[1-3]。
随后发展起来的合成孔径雷达干涉测量(interferometric synthetic aperture radar,InSAR)技术也为获取球面表面的数字高程模型(digital elevation model,DEM)提供了一种全新的高精度测量方法。该方法利用雷达电磁波的干涉相位信息进行地表信息提取,相比立体摄影测量方法能获取更高的测距精度。InSAR技术的使用起源于美国喷气推进实验室,Rogers等[4]利用干涉技术探测金星和月球地形;Graham[5]证明了利用干涉几何可获取足够数量的点来描述地形表面并将该技术用于地形制图;Zebker等[6]在加州帕萨迪纳喷气推进实验室进行了第一次实际的干涉实验,发表了用机载双天线SAR进行地形测绘的结果,并提出了该技术存在的局限性并对干涉算法进行了改进。自此,InSAR技术受到国内外众多学者的关注,并逐渐走向成熟,成为获取DEM的重要技术之一。
由于SAR在各领域得到广泛应用,自美国发射的第一颗星载SAR卫星Seasat开始,世界各国相继发射各自的SAR卫星,2016年8月中国在太原卫星发射中心用长征四号丙运载火箭成功发射GF-3卫星[7],该卫星已初步具备干涉成像的能力,但由于卫星平台轨道控制技术的限制,利用高分三号卫星影像进行InSAR数据处理仍存在较多挑战。本文对InSAR数据处理过程中关键技术进行研究,并利用GF-3卫星数据应用InSAR技术提取试验区域DEM,验证其干涉成像能力。
1 GF-3卫星成像模式GF-3卫星是中国高分辨率对地观测系统重大工程中唯一的微波成像民用卫星,也是中国首颗1 m分辨率C频段多极化SAR卫星[8]。GF-3以太阳同步的黄昏-黎明轨道绕地球运行,高度755 km,倾角98.411°,轨道重复周期约29 d。它具有高分辨率成像、大成像宽度、高幅度精度、多成像模式等特点。其卫星平台指标如表 1所示。
| 表 1 GF-3卫星平台指标 Tab.1 Platform Indicators of GF-3 Satellite |
 |
GF-3卫星也是世界上成像模式最多的SAR卫星,共具有12种成像模式。主要包括:条带成像模式,该模式下天线的指向不随雷达平台的移动而变化,天线匀速扫过地面,得到连续的图像;扫描成像模式,通过在多个子测绘带间来回切换来实现大幅宽成像;滑动聚束成像模式,通过控制天线辐照区在地面的移动速度来控制方位分辨率;波成像模式通过对大面积、均匀的地球表面进行离散采样,获取一系列离散图像,且其成像区域为方形,沿方向位等间隔分布等。此外,GF-3卫星还可在聚束、条带、波浪、全球观测等多种成像模式下实现自由切换,达到“一星多用”的效果。
2 InSAR数据处理InSAR技术的基本原理是利用具有干涉成像能力的两部SAR天线(或一部天线重复观测)来获取同一地区具有一定视角差的两幅具有相干性的单视复数(single look complex,SLC)影像,利用其干涉相位信息获取地表高程信息。随着InSAR技术的逐渐成熟,由InSAR技术获取DEM的流程也已基本成型,具体如图 1所示。
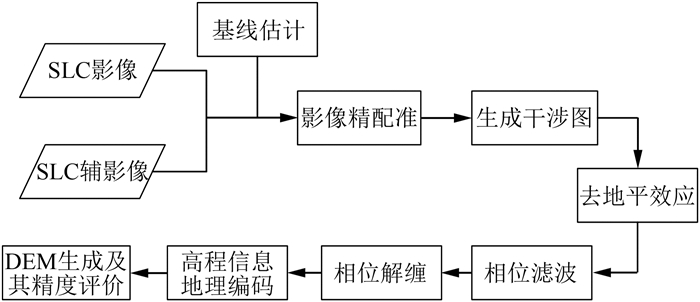 |
| 图 1 InSAR提取DEM流程图 Fig.1 Flow Chart of InSAR Extracting DEM |
本文将针对处理中的影像精配准、相位滤波、相位解缠等关键技术进行讨论。
2.1 影像精配准影像配准是指将含有相同场景或目标的SAR图像进行空间几何对准的过程。InSAR处理过程中,为保证干涉图的质量以及最终DEM的精度,影像的配准精度一般要求达到亚像素级别。本文采用基于卫星精密轨道数据的影像配准方法[9],该方法主要分为粗配准、像元级配准和亚像元级配准。经精配准后配准精度可达1/8个像元,满足InSAR配准精度要求。
2.2 相位滤波为获得更好的相位解缠效果以提高DEM精度,在解缠之前需要对干涉图进行相位滤波操作,减小影像中存在的噪声对解缠的干扰。目前常用的相位滤波方法主要可以分为空间域滤波和频率域滤波。其中常用方法包括:
1) Boxcar滤波[10]。它是一种滑动窗口内取平均像素值的滤波方法,对于单通道SAR图像,滤波后的像素值Xi, j与滑动串口内的像素值的关系:
| $ X_{i, j}=Y_{i, j} \frac{1}{N^{2}} \sum\limits_{p=-(N-1) / 2}^{N / 2} \sum\limits_{q=-(N-1) / 2}^{N / 2} Y_{i+p, j+q} $ | (1) |
式中,N为滤波窗口的尺寸;i、j分别为图像中被滤波的像素所在的行、列号。
2) Goldstein滤波[11]。它首先对得到的干涉图进行分块,然后对已经分好的小块干涉图进行傅里叶变换,最后到它的频谱,再根据平滑处理的幅值对各个小块干涉图进行处理。该方法对相互重叠的滑动窗口的傅里叶谱进行平滑:
| $ Z^{\prime}(u, v)=S\{|Z(u, v)|\} \cdot Z(u, v) $ | (2) |
式中,S{}为平滑算子;u和v为空间频率。通过对平滑后的傅里叶因子进行逆傅里叶变换即可得到滤波结果。
3) 自适应滤波[12]。它是在进行滤波处理时,其滤波器参数会自动根据之前已获得的滤波器参数等结果进行调节。
2.3 相位解缠相位解缠是指将相位由主值或相位差值恢复为真实值的过程,是InSAR数据处理过程中的关键步骤,解缠结果将直接影像DEM精度。目前所有的解缠结果均可以分为两个步骤:①计算解缠相位的相位梯度估算值;②对相位值进行积分。根据积分方法的不同,解缠方法主要可以分为3大类:路径跟踪法(包括枝切法、区域生长法等)、最小范数法[13, 14](包括多网格算法、Picard迭代法等)、基于网络规划的相位解缠算法(包括MCF(minimum cost flow)法等)。本文主要利用区域生长法、MCF法进行试验分析。区域生长法从高质量的相位数据出发,沿动态路径进行相位解缠所确定的路径均是高可信度的解缠路径;MCF法是为相干图选取一个阈值,提取出所有相干系数高于该阈值的相位,建立一个Delaunay三角网,构建其对偶图,并在源三角网中求得残差将其映射到对偶网络中,在对偶网络中,应用MCF方法链接各正负残差点对,计算MCF集合,对相位矩阵进行积分, 得到解缠结果, 再从高质量区域向低质量区域进行积分, 得到全局结果。
3 实验与分析 3.1 试验数据本试验采用国产GF-3卫星精细条带I模式下L1级产品数据,数据包括一个XML格式头文件和一个TIFF格式影像文件。头文件中包含卫星传感器信息、平台信息、轨道点信息、影像信息等。
干涉影像对覆盖区域主要位于中国河南省登封市西部及北部嵩山区域,见图 2红框内区域。
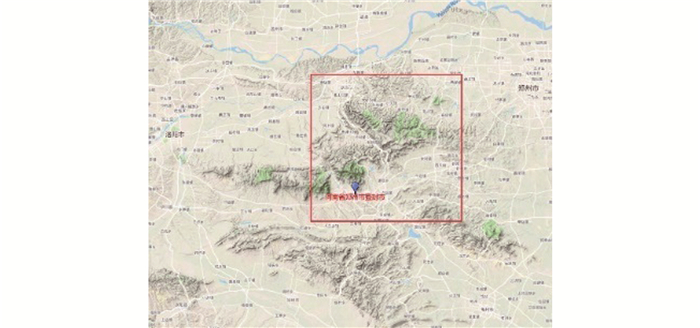 |
| 图 2 试验区域地形图 Fig.2 Topographic Map of Test Area |
试验区域为覆盖大面积山体,地形起伏较大,适合进行实验。干涉像对信息如表 2所示。
| 表 2 干涉对影像信息 Tab.2 Information of Interference Image Pair |
 |
3.2 干涉实验
为评价干涉像对的质量,首先对干涉像对进行基线估计,计算其基线、轨道偏移和其他系统参数。经基线估计后,试验数据基线长度为634.538 m,时间基线为29 d。在配准之前,对原始影像对做方位向和距离向的预滤波处理,以减少斑点噪声对配准精度的影响。本实验中采用多视处理滤波方法,处理得到干涉像对强度图如图 3所示。
 |
| 图 3 干涉像对强度图 Fig.3 Intensity Map of Interference Image Pair |
为凸显试验效果,后续试验截图均为局部放大图,放大部分见图 3(a)红框内。
在影像配准阶段,本试验采用基于外部DEM的配准方法。参考DEM为SRTM3 version4数据。SRTM数据由美国航空航天局(National Aeronautics and Space Administration,NASA)在2000年利用奋进号航天飞机上的雷达测观测所得,是目前最常用的高程数据之一,有SRTM1和SRTM3两种。目前公开的覆盖中国区域的只有SRTM3,精度为90 m。同时version4相对version2使用了新的插值算法和更好的辅助调制解调器,对无值区域用辅助数据做了填充之后,生成干涉图,采用的多视处理为2∶2,同时对干涉图进行去地平效应处理。由于雷达影像中存在较多斑点噪声,为减少噪声对后续相位解缠的影响,需要对干涉图进行滤波处理,本试验分别采用GoldStein滤波、Boxcar滤波、自适应滤波3种方法进行处理并进行对比分析。试验结果如图 4所示。
 |
| 图 4 干涉图结果及相干系数图 Fig.4 Results of Interferogram and Coherent Coefficient Map |
由图 4(c)、4(d)、4(e)可以看出,3种滤波方法都能够有效地减少干涉图中的噪声。其中Goldstein滤波方法处理结果最好,在滤除噪声的同时保持了相位波形的形状,干涉条纹最为清晰,边缘平滑,区分明确;Boxcar滤波方法虽然去噪效果良好,但干涉条纹边缘杂乱,且丢失了干涉图中部分有效信息;自适应滤波方法去噪效果相对较差,干涉条纹杂乱,存在变形和位移的情况。故本实验选取Goldstein滤波处理后数据结果进行下一步处理。
对相干系数图中的值进行统计,其中最大值为0.994 9,平均值为0.393 5,标准差为0.191 8。在相干图中越亮的区域相干性越高,越暗的区域相干性越低。从图 4(f)中可以看出,右上角地势相对平坦的区域相干性较高,而在中部、右下角等地形复杂的山区相干性较低。
对滤波后的干涉图做相位解缠、轨道精化和重去平后处理后结果如图 5所示。本试验分别采用MCF法和区域生长法进行相位解缠,解缠阈值均设为0.15。
 |
| 图 5 解缠结果 Fig.5 Results After Phase Unwrapping |
对比可见,对于本实验数据,区域生长法的解缠效果优于MCF法,该解缠结果沉降区域清晰可见,色彩的连续性和平滑性也较好,同时重去地平后的干涉图条纹边缘更加平滑。
最后利用区域生长法解缠结果通过相位高程转换及地理编码得到最终解求的数字高程模型,并对结果进行三维展示,如图 6所示。
 |
| 图 6 试验结果 Fig.6 Results of the Test |
由此,本次实验利用国产GF-3卫星影像成功恢复试验区域的地形结构,获取了试验区域的DEM,DEM整体效果良好。
3.3 DEM精度评价依次对提取的DEM做定性、定量分析对其精度进行评价。首先将干涉试验中提取的DEM透明半叠加到Google Earth上,验证DEM结果相对试验区域是否存在水平偏移。结果如图 7所示。
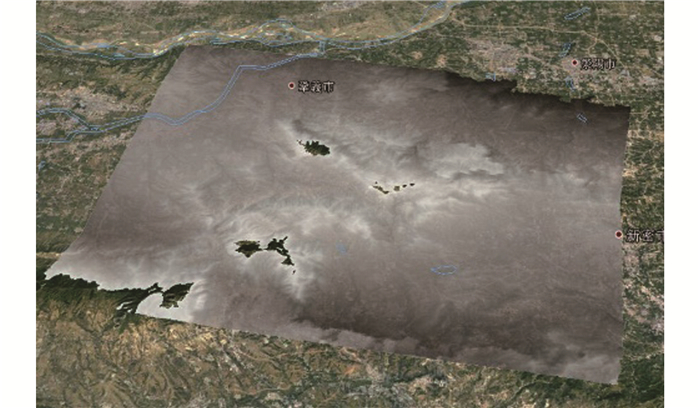 |
| 图 7 DEM叠加效果图 Fig.7 DEM Overlay Effect Map |
从图 7可以看出,提取的DEM与试验区域基本吻合,无较大水平、垂直偏移。
之后从试验区域选择均匀分布的10个点,获取DEM中高程值并与参考DEM中的高程值进行对比分析,如表 3所示。
| 表 3 高程值对比 Tab.3 Comparison of Altitude Values |
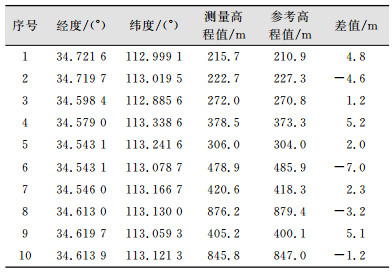 |
由以上10个点求得高程中误差为4.08 m。
4 结束语国产GF-3卫星已初步具备干涉成像能力,利用GF-3卫星影像可以成功提取影像范围内的DEM。现有的影像配准、相位滤波、相位解缠等技术方法对GF-3数据亦可适用并达到不错的效果。但依然存在以下几个问题:
1) 对于GF-3InSAR处理,由于实时定轨精度较差,基线误差较大,导致方位角调制误差和范围内的坡度误差,不利于实时生成数字高程模型;
2) 当影像内存在复杂地形或噪声较多时,相干性较差,影响后续解缠效果;
3) 解缠过程中,由于噪声无法避免以及目前解缠技术的限制,解缠结果中依然存在一些无值区域,尤其在低相干区域,影响DEM精度。
目前,InSAR处理过程中各关键技术算法在处理国产GF-3卫星影像时依然存在各方面的局限性,后续需要研究更适应于国产SAR卫星数据的算法,充分挖掘和拓展国产SAR卫星数据的用途。
| [1] |
卢莹, 颜意庆, 杨俊凯, 等. 不同分辨率DEM对InSAR变形监测精度的影响分析[J]. 测绘地理信息, 2018, 43(6): 106-109. |
| [2] |
Tarquis A M, Platonov A, Matulka A, et al. Application of Multifractal Analysis to the Study of SAR Features and Oil Spills on the Ocean Surface[J]. Nonlinear Processes in Geophysics, 2014, 21(2): 439-450. DOI:10.5194/npg-21-439-2014 |
| [3] |
Margarit G, Mallorqui J J, Lopez-Martinez C. Grecosar, a SAR Simulator for Complex Targets: Application to Urban Environments[C]. IEEE International Geoscience & Remote Sensing Symposium, Barcelona, Spain, 2007
|
| [4] |
Rogers A E, Ingalls R P. Venus: Mapping the Surface Reflectivity by Radar Interferometry[J]. Science, 1969, 165(3 895): 797-799. |
| [5] |
Graham L C. Synthetic Interferometer Radar for Topographic Mapping[J]. Proceedings of the IEEE, 2005, 62(6): 763-768. |
| [6] |
Zebker H A, Goldstein R M. Topographic Mapping From Interferometric Synthetic Aperture Radar Observations[J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B5): 4 993-5 002. DOI:10.1029/JB091iB05p04993 |
| [7] |
姚天宇. 长征四号丙运载火箭成功发射GF-3卫星[J]. 中国航天, 2016(8): 8. |
| [8] |
Bing H, Chibiao D, Lihua Z, et al. The GF-3 SAR Data Processor[J]. Sensors, 2018, 18(3): 835-839. DOI:10.3390/s18030835 |
| [9] |
刘广, 郭华东, 范景辉. 基于外部DEM的InSAR图像配准方法研究[J]. 遥感技术与应用, 2008(1): 72-76. |
| [10] |
Lee J S, Cloude S R, Papathanassiou K P, et al. Speckle Filtering and Coherence Estimation of Polarimetric SAR Interferometry Data for Forest Applications[J]. Geoscience & Remote Sensing IEEE Transactions on, 2003, 41(10): 2 254-2 263. |
| [11] |
Goldstein R M, Werner C L. Radar Interferogram Filtering for Geophysical Applications[J]. Geophysical Research Letters, 1998, 25(21): 4 035-4 038. DOI:10.1029/1998GL900033 |
| [12] |
Wagner C, Wittum G. Adaptive Filtering[J]. Numerische Mathematik, 1997, 78(2): 305-328. DOI:10.1007/s002110050314 |
| [13] |
孙龙, 胡茂林, 张长耀. InSAR相位解缠最小二乘算法的研究[J]. 雷达科学与技术, 2005, 3(4): 216-220. DOI:10.3969/j.issn.1672-2337.2005.04.006 |
| [14] |
许才军, 王华. InSAR相位解缠算法比较及误差分析[J]. 武汉大学学报·信息科学版, 2004, 29(1): 67-71. |
 2021, Vol. 46
2021, Vol. 46

