| DDA算法在地表面积计算中的应用研究 | [PDF全文] |
2. 武汉大学精密工程与工业测量重点实验室, 湖北 武汉, 430079
2. Key Laboratory of Precision Engineering and Industrial Measuring, Wuhan University, Wuhan 430079, China
随着三维可视化技术的快速发展,建立在数字化、可视化、可测量基础上的三维地形越来越多地被各行各业所关注利用[1]。在三维地形数字分析中,涉及较多的数据是地表面积,但是由于地形起伏,难以用数学函数拟合,不能直接计算[2]。
对于地表三维空间面积计算,工作人员需要在给定的栅格数据上圈定任意范围来计算其地表三维面积。有学者给出该类问题的解决方法,有两种基本思路。一种思路是将栅格数据分成完整栅格和非完整栅格两部分单独求取各部分面积,两者加和求取总地表面积,这种方法差异在对非完整栅格的处理上,有构建三角网方法[3]和边界获取最小矩形法[4]。另一种思路是将栅格数据作为一个整体计算地表面积,有递归三角形构网法[5]、一个像素分为两个三角形法[6]、不断分割多边形法[7]及一个像素格分为8个空间三角形法[8]。相比之下,对栅格数据进行整体处理的方法在使用效率方面不占优势且判定条件太多,而将栅格数据分成两部分进行处理,前人研究结果无法平衡精确度和算法的复杂度,因此,笔者提出了一种新的解决思路。
笔者将栅格数据分成两部分进行计算。针对完整栅格进行分割,结合海伦公式对地表三维面积进行累加计算;针对不完整栅格采用计算机图形学中DDA算法[9]计算交点坐标(一种基于直线的微分方程来生成直线的方法),通过射线法判断点在多边形内还是在多边形外并相应计算面积。利用实际数据对该算法进行验证,从数据类型及算法效率上对结果进行解释分析。
1 基于DDA算法计算地表面积的方法及步骤首先,笔者对任意多边形进行内部重构格网,对于得到的完整格网笔者将每个格网划分成4个小三角形,利用海伦公式计算求和,最后累加即可;对于非完整格网笔者利用DDA算法依据步进求出多边形边与格网的交点坐标,依据双线性内插获得交点高程值,依据射线法判断点是否在多边形内,以此通过交点坐标结合其接近点来求取四边形面积(将该四边形划分为两个三角形)。具体步骤如下所示:①读取任意封闭区域范围,生成对应封闭矩形区域;②将坐标(B, L, H)转换为(X, Y, Z);③任意封闭区域与封闭矩形区域作交,得到完整格网与非完整格网;④计算完整栅格地形表面积;⑤计算非完整栅格的地形表面积;⑥两部分计算面积之和即为任意封闭区域的地形表面面积。
1.1 计算完整栅格面积首先,要统计完整栅格个数,本程序通过判断是否存在高程值来确定完整栅格;其次,将单位栅格分割成4个小三角形来拟合小栅格的地形表面面积;最后,将这些完整栅格的面积按照栅格统计个数累加即可求得完整栅格的地形表面面积。
对于一个单元栅格,笔者将其分割成4个三角形,分割点为栅格中心点。栅格中心点的高为栅格4个顶点高程值的平均值,中心点的长宽为单位栅格长宽一半。根据空间关系可以确定栅格4个顶点到该中心点的空间距离。示意图如图 1所示。
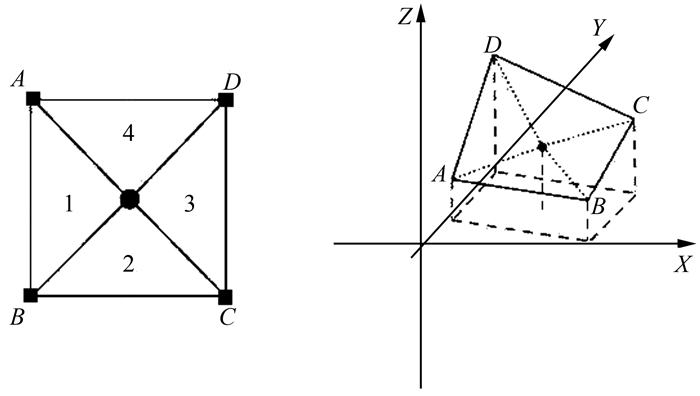 |
| 图 1 单元栅格分割示意图 Fig.1 Unit Grid Split Schematic Diagram |
基于单位整格网构建4个三角形后,依据海伦定理计算每个三角形面积,加和得到单元格网地表面积、地表面积与两点间的空间长度分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {{S_{ABC}} = \sqrt {S(S - a)(S - b)(S - c)} }\\ {S = \frac{1}{2}(a + b + c)}\\ {{S_{ij}} = \sqrt {{{\left( {{X_j} - {X_i}} \right)}^2} + {{\left( {{Y_j} - {Y_i}} \right)}^2} + {{\left( {{Z_j} - {Z_i}} \right)}^2}} } \end{array}} \right. $ | (1) |
式中, a、b、c为三角形的边长;两点的空间直角坐标为(Xi, Yi, Zi)和(Xj, Yj, Zj)。
1.2 计算非完整栅格面积结合DDA算法特性,对于多边形每一条边上的两个顶点所在的直线,按照步长总数逐次求解该直线与网格两个交点P1(X1, Y1)和P2(X2, Y2)的平面坐标。主要计算思路和步骤如下:
1) 计算出直线P1P2在X轴和Y轴上所经过步长总数为:
| $ \left\{ {\begin{array}{*{20}{l}} {{S_X} = \left( {{X_2} - {X_1}} \right)/{p_X}}\\ {{S_Y} = \left( {{Y_2} - {Y_1}} \right)/{p_Y}} \end{array}} \right. $ | (2) |
式中,pX为网格上每个格子沿X轴的增量;pY为沿Y轴的增量;SX为直线在X轴上的步长,SY为直线在Y轴上的步长。
2) 以最大步长Smax作为基准, 计算出直线P1P2沿X轴和Y轴的增量dX和dY为:
| $ \left\{ {\begin{array}{*{20}{l}} {{d_X} = \left( {{X_2} - {X_1}} \right)/{S_{\max }}}\\ {{d_Y} = \left( {{Y_2} - {Y_1}} \right)/{S_{\max }}} \end{array}} \right. $ | (3) |
由于直线具有方向性,因此, 在计算增量的时候,需要考虑dX和dY的正负性。
3) 计算相邻两点Pi和Pi+1坐标为:
| $ \left\{ {\begin{array}{*{20}{l}} {{P_i} = \left( {{X_1} + {d_X} \times i, {Y_1} + {d_Y} \times i} \right)}\\ {{P_{i + 1}} = \left( {{X_1} + {d_X} \times (i + 1), {Y_1} + {d_Y} \times (i + 1)} \right)} \end{array}} \right. $ | (4) |
4) 求解Pi和Pi+1相邻两点构成的非完整格网区域。直线斜率对直线增长影响如图 2所示,当|k|≤1时候,直线在X轴上以一个整格子增长;当|k|>1时候,直线在Y轴上以一个整格子增长。
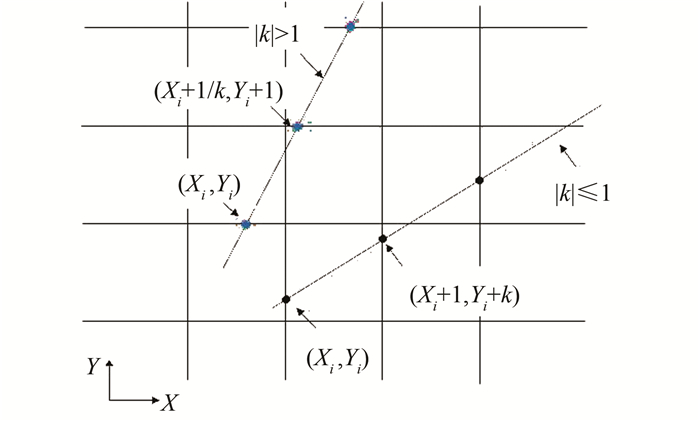 |
| 图 2 直线斜率控制步长 Fig.2 Linear Slope Control Step Length |
考虑直线的增长模式(沿着X轴或者Y轴增长),直线在网格上的交集只会出现两种模式:一种为2个交点都在1个格网中;另一种为2个交点分别在2个相邻的格网中。
以X轴为参考,直线会出现斜交于X轴(图 3(a))及平行于X轴(图 3(b)),当Pi和Pi+1在X轴上以一个整格子增长,这两点在同一格网中或者不在同一格网中。由图 3(a)可知,在该直线左侧,点P1(Xi, YI)与点P2(Xi+1, Yi+k)沿X轴方向在相邻的两个格网中;在该直线的右侧,点P1与点P2沿X轴方向在同一格网中。由图 3(b)可知, 对于平行于X轴时,点P1(Xi, Yi)与点P2(Xi+1, Yi)沿X轴方向在同一格网内。
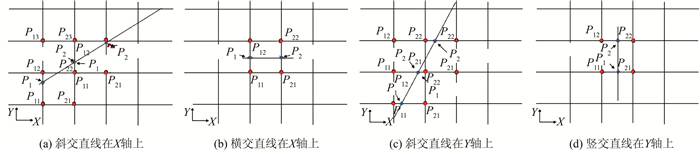 |
| 图 3 斜交直线在坐标轴上以一个整格子增长 Fig.3 Oblique Line Is Growing on the X-Axis with a Whole Grid |
以Y轴为参考,直线会出现斜交于Y轴(图 3(c))及平行于Y轴(图 3(d)),当点Pi和点Pi+1在Y轴上以一个整格子增长时,这两点在同一格网中或者不在同一格网中。由图 3(c)可知,在该直线左侧,点P1(Xi, Yi)与点P2(Xi+1/k, Yi+1)沿Y轴方向在同一格网中;在该直线的右侧,点P1与点P2沿Y轴方向在相邻两个格网中。由图 3(d)可知,对于平行于Y轴的情况,点P1(Xi, YI)与点P2(Xi, Yi+1)沿Y轴方向在同一格网内。
通过以上分析可以看出,点Pi和点Pi+1将参考格网分为左右或上下两部分。笔者通过射线算法[10]判断哪一部分的顶点在多边形内部,以此来确定笔者需要求面积的不完整格网。由于点Pi和点Pi+1在多边形的边上,当点Pi和点Pi+1在同一格网时,通过其他最多2个点就能确定需要计算面积的不完整栅格部分;当点Pi和点Pi+1在相邻的两个格网上时,通过其他最多3个点就可以确定需要计算面积的不完整栅格部分。
射线算法是计算机图形学中,判断点是否在多边形内的一种实现思路。主要思路是以点P为端点,向左方做射线L,然后沿着L从无穷远处开始向点P移动,当遇到多边形的某一条边时,记为与多边形的第一个交点,表示进入多边形内部,继续移动,当遇到另一个交点时,表示离开多边形内部。由此可知,当L与多边形的交点个数是偶数时,表示点P在多边形外;当L与多边形交点个数是奇数时,表示点P在多边形内部。
2 实验及结果分析实验使用的测试数据为栅格数据,在ArcGIS里进行测量计算,可以得到该区域完整栅格的面积。在本程序中,笔者通过ArcGIS获取多边形地形栅格数据的矢量格式并提取多边形的顶点坐标,作为录入数据之一,可以得到包含不完整栅格的总体区域面积。
实验采用的原始数据行数为8 915、列数为13 438,3个波段真彩色杭州影像图,栅格单元长宽都为20.009 917 45 m。本次实验一共做了23组对比测试,依据对原始数据圈定不同边数,不同区域大小,分别求取其投影平面面积及三维地形面积。笔者借助ArcGIS平台[11]对同样数据进行测量计算(记为A),并与本程序测量结果(记为B)做对比,总结出规律,结合数据类型转换,对结果进行解释。
第1组测试,从原始数据中截取多边形中边数最少的三角形,不包含高程为0区域;第2组测试,从原始数据中截取四边形,测试数据包含了高程值为0区域;第3组测试,从原始数据中截取五边形,测试数据包含了高程值为0区域。计算三角形、四边形和五边形的2维及3维面积,将得到的结果与在ArcGIS中计算出的结果进行比较,计算差异百分比,得到表 1的差异统计结果。
| 表 1 三角形、四边形和五边形的面积误差 Tab.1 Triangle, Quadrilateral, and Pentagon Area Error |
 |
从表 1可以看到,3组的面积差异同时存在于2维面积和3维面积中,本程序计算的结果总是比ArcGIS计算的结果大,并且差异百分比均不超过1%。第2组四边形和第3组五边形的测试中还发现,当所计算区域包含高程值为0的区域后,3维面积结果与ArcGIS基本一样。
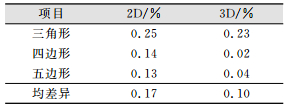
笔者将这3组测试数据的结果进行汇总,计算出整体差异百分比,结果如表 2所示,很明显看到2维和3维面积平均差异都不超过1%,且本程序计算结果总是比ArcGIS计算结果大。理论上由于笔者在栅格数据上画多边形时保留边缘,因此,笔者计算的总体面积比ArcGIS的结果必然要大一些。这种规律明显的测试结果,与理论上是一致的,说明笔者的结果可接受,计算结果更精确。
| 表 2 多边形面积误差 Tab.2 Polygonal Area Error |
 |
3 结束语
本文重点阐述了地形表面面积的计算理论及步骤,从实际计算结果分析了计算的精度,并对计算结果呈现的明显规律进行解释。经过实际验证,提出对于不完整栅格面积计算的思路简单可行,可对地形表面面积计算提供有价值的参考。
| [1] |
乔志勇, 徐敬仙. 三维规划辅助决策系统研究[J]. 测绘地理信息, 2015, 40(4): 90-92. |
| [2] |
钟登华, 李明超, 王刚, 等. 水利水电工程三维数字地形建模与分析[J]. 中国工程科学, 2005, 7(7): 65-70. DOI:10.3969/j.issn.1009-1742.2005.07.012 |
| [3] |
韩买侠, 程传录, 王维. 地表面积计算方法研究[J]. 测绘通报, 2015(9): 72-74. |
| [4] |
谢成磊, 赵荣, 梁勇. 基于地理坐标的地理国情统计单元表面面积精确计算[J]. 遥感信息, 2014, 29(4): 47-51. DOI:10.3969/j.issn.1000-3177.2014.04.010 |
| [5] |
魏东, 张秀程. 基于递归算法的三维地形面积计算方法研究[J]. 工程地质计算机应用, 2007, 47(3): 5-7. |
| [6] |
江帆, 吕晓华, 王仲兰. 基于复化公式的DEM表面积算法分析[J]. 测绘学院学报, 2005(4): 263-265. DOI:10.3969/j.issn.1673-6338.2005.04.009 |
| [7] |
王长海. DEM模型的三维地表面积算法研究[J]. 红水河, 2010, 29(3): 153-154. DOI:10.3969/j.issn.1001-408X.2010.03.042 |
| [8] |
Jenness J S. Calculating Landscape Surface Area from Digital Elevation Models[J]. Wildlife Society Bulletin, 2004, 32(3): 829-839. DOI:10.2193/0091-7648(2004)032[0829:CLSAFD]2.0.CO;2 |
| [9] |
张义宽. 计算机图形学[M]. 西安: 西安电子科技大学出版社, 2004.
|
| [10] |
苗春葆. 点与多边形关系的射线法[J]. 电脑编程技巧与维护, 2008(3): 56-58. DOI:10.3969/j.issn.1006-4052.2008.03.011 |
| [11] |
吴秀琴, 张洪岩, 李瑞改, 等. ArcGIS9地理信息系统应用与实践[M]. 北京: 清华大学出版社, 2008.
|
 2019, Vol. 44
2019, Vol. 44

