| 基于轮廓纵向膨胀的核安全壳裂缝提取算法 |
2. 武汉大学精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉, 430079
2. Key Laboratory of Precise Engineering & Industry Surveying, National Adminstration of Surveying, Mapping and Geoinformation, Wuhan University, Wuhan 430079, China
核电站安全壳作为保证核电生产安全的关键性建筑,不仅受自然因素的侵蚀作用,还不可避免地经常处于高温高压等极端环境下,因此,安全壳表面裂缝的检测成为核电工业安全防护的重点。图像上裂缝的特征提取技术是核安全壳裂缝自动检测的关键。
由于安全壳墙体表面受到自然因素的影响,因此污迹、剥落和凹凸坑较多,裂缝图像噪声密集。同时还受到人工因素的影响,形态和裂缝相似的修补痕迹成为裂缝提取的强干扰。且裂缝宽度在0.05~0.3 mm之间,裂缝信息量占全图信息量比例极小,与墙面背景的对比度低,提取难度较大。传统的图像边缘检测算法包括Prewitt算子、Sobel算子、Canny算子等能对特定方向上的边缘做出最大响应,但去噪能力差,对于高噪声、强干扰的安全壳墙体裂缝图像,很难保证裂缝提取的正确性和完整性[1]。文献[2]提出了一种基于BP神经网络的分块图像特征提取方法;文献[3]提出了一种基于视觉模型的仿生学裂缝检测算法;文献[4]提出了一种基于数学形态学原理进行裂缝检测的方法;文献[5]提出了两种基于偏微分方程的裂缝增强方法。这些方法需要选择较好的训练模型,要求裂缝本身的信息足够强,不适于安全壳高噪声背景图像中极其细微裂缝的提取。为此,针对核电站安全壳高噪声裂缝图像[6-18],本文提出一种基于轮廓纵向膨胀去噪的裂缝提取算法,即利用裂缝区别于非目标点群的形态特征——整体连续性,对点群进行纵向膨胀操作,基于轮廓的长度、面积和形心比等形态参数计算裂缝判断置信度,以此滤除大量的噪声和相似性干扰点群,正确提取出裂缝。
1 轮廓纵向膨胀去噪在提取裂缝基础信息的同时,大量的噪声和相似性干扰被遗留,本文通过轮廓纵向膨胀算法进行去噪。裂缝在整体上具有较强的连续性,在微小区域内裂缝点的方向趋于一致。而噪声点群是散乱的、随机分布的,在整体上不能成为线状,在微小区域内方向各异,成团分布。在图像上寻找轮廓时,裂缝片段呈现连续狭长的形态,通过轮廓的长度、面积和形心比3种形态参数可以表征裂缝片段的形态特征,以此可以滤除大量非目标噪声。
1.1 方向小波裂缝基础信息提取传统的经典边缘检测算法难以完整地提取出裂缝的基础信息,因而多尺度的边缘检测是必要的。方向小波裂缝提取算法[19, 20]本身具有多尺度特征,适用于背景复杂的高噪声图像。将图像信息从空间域转化到频域,背景信息集中在低频和中频,裂缝信息集中在高频,对小波信号进行伸缩平移,在低频域进行频率上的细分,在高频域进行时间上的细分,并进行方向分析。方向小波变换定义为:
| $ \begin{array}{l} {W_{{2^j}}}^xf(x, y{\rm{)}} = \\ \frac{1}{{K\pi {\sigma ^2}}} \times f\left( {x, y} \right) \times x \times {\rm{exp}}(\frac{{\sqrt {{x^2} + {y^2}} }}{K}) \end{array} $ | (1) |
式中,2j为小波变换的尺度;W2jxf(x, y)为在图像f(x, y)中的二维小波变换结果;(x, y)为图像像点坐标;f(x, y)为像点灰度值;σ2为高斯函数方差;K=-4j2σ2。
1.2 裂缝纵向膨胀由于在裂缝基础信息的提取过程中,裂缝有少部分信息丢失,导致裂缝点群区域在二维图像平面上并非严格连通,在生成轮廓时形成了轮廓的断裂,对轮廓形态参数的计算有较大影响,因此,在生成轮廓之前,需先对图像进行轻微膨胀操作,使断裂或者被分割的裂缝片段融合在一起,形成连通的区域,使裂缝的轮廓呈现连续细长的形态。
普通的全向膨胀方法在连通裂缝片段的同时将噪声点群多次膨胀并使其联结成团,成为面积与裂缝相近的中小型轮廓,从而影响面积参数发挥过滤作用。为此,本文提出了一种改进后的裂缝有向膨胀的算法——纵向膨胀。由于裂缝在图像上表现的纵向方向性较强,因此可以得到较好的膨胀效果。
本文设计了三种膨胀卷积核,如图 1所示。在水平横向上膨胀度为0,纵向膨胀度为7,上膨胀卷积核的参考点位置在(0, 0),仅在向上的方向膨胀;下膨胀卷积核的参考点位置在(0, 6),仅在向下的方向膨胀;双向膨胀卷积核的参考点位置在(0, 3),做纵向膨胀。膨胀效果如图 2所示。
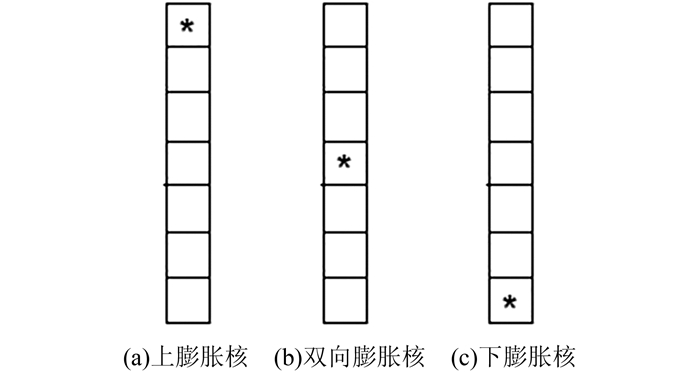 |
| 图 1 纵向膨胀卷积核 Figure 1 Longitudinal Expansion Kernel |
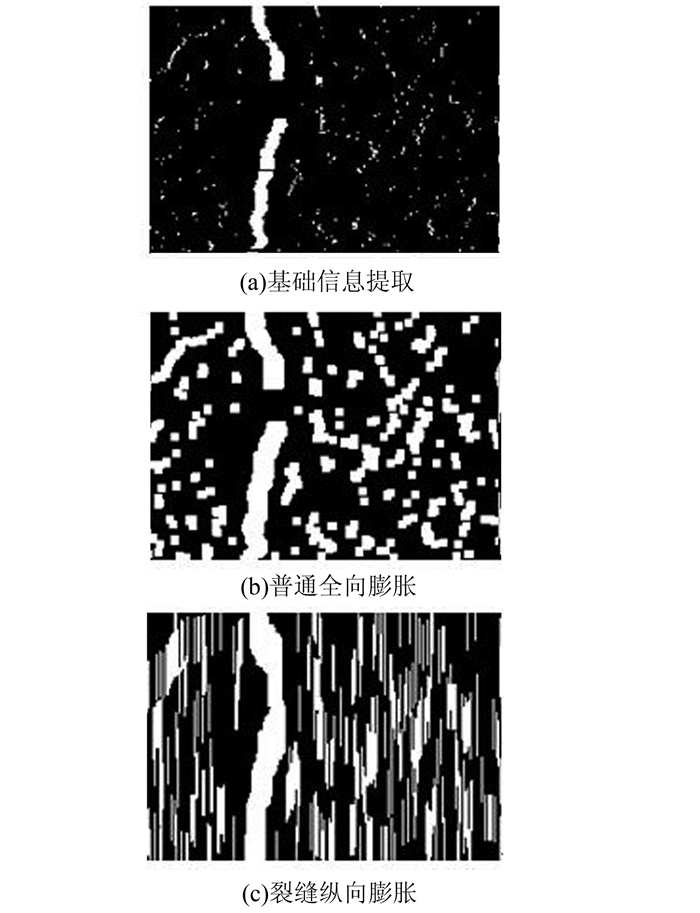 |
| 图 2 纵向膨胀与普通全向膨胀效果对比图 Figure 2 Comparison of Longitudinal Expansion and General Expansion |
1.3 多特征融合滤波
经过纵向膨胀的裂缝有三种形态学特征:裂缝的轮廓长度较长;面积在一定范围内;形心比与圆的形心比差值较大。计算长度、面积和形心比等3种轮廓形态参数,并以此为标准滤除大量噪声。
轮廓面积与周长通过轮廓矩进行计算,轮廓矩Mm, n的计算公式为:
| $ {M_{m, n}} = \int {\int {{x^m}{y^n}f{\rm{(}}x, y{\rm{)d}}x{\rm{d}}y} } $ | (2) |
式中,(m, n)是二阶矩;(x, y)是像素点坐标。
面积S的计算公式为:
| $ S = {M_{0, 0}} $ | (3) |
长度h的计算公式为:
| $ h = S/w $ | (4) |
式中, w为横向平均宽度。
形心比计算公式为:
| $ {A_{{\rm{Centroid}}}} = \frac{{4{\rm{ \mathit{ π} }}S}}{{L \times L}} $ | (5) |
裂缝判断置信度为:
| $ {A_{{\rm{Confidence}}}} = \frac{{\left| {{A_{{\rm{Centroid}}}}-1} \right| \times h}}{{S-{S_0}}} $ | (6) |
式中, L为轮廓链的周长; S为轮廓面积; S0为裂缝片段的最佳面积。
轮廓越狭长,判断为裂缝的置信度越高,成为裂缝的可能性越大。以裂缝判断置信度为标准滤除非目标噪声,得到裂缝的轮廓,效果如图 3所示。
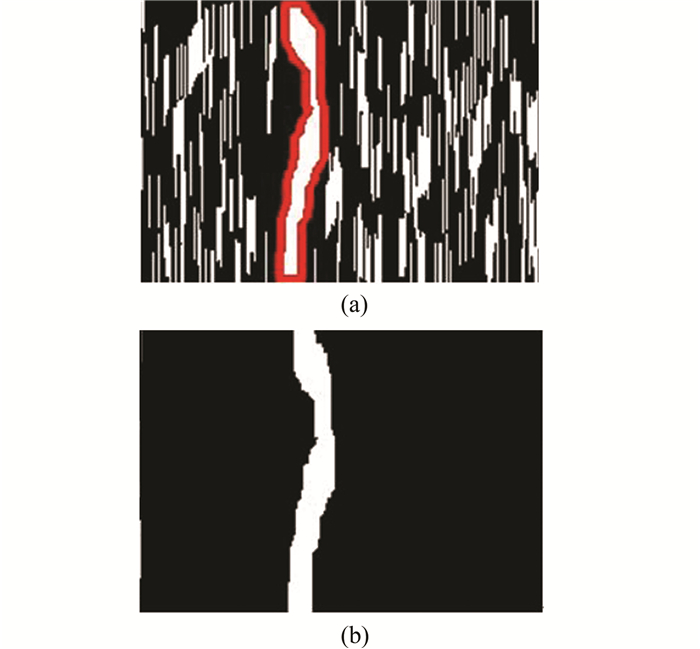 |
| 图 3 轮廓特征过滤 Figure 3 Contour Feature Filtering |
经过轮廓纵向膨胀过滤后的裂缝图像在保留绝大部分裂缝点群的同时滤除了大量噪声。少量非目标点群在形态上与裂缝相似,或与裂缝相距很近,不可避免地遗留下来。通过裂缝追踪连接裂缝片段,根据长度可正确地识别裂缝曲线,根据裂缝初步位置映射到原始图像,加密裂缝点群,从而提取完整裂缝。
2 实验结果与分析 2.1 核壳裂缝特征提取算法设计本文设计了基于轮廓纵向膨胀的核安全壳裂缝提取算法。首先通过方向小波变换提取裂缝基础信息,利用轮廓纵向膨胀去噪算法滤除团状噪声和孤立点噪声,追踪得到真正的裂缝曲线,并映射到原始图像进行裂缝点群加密,提取完整裂缝。算法流程如图 4所示。
 |
| 图 4 核安全壳裂缝提取算法流程 Figure 4 Process of Cracks Extraction Algorithm for the Containment of Nuclear Power Plant |
2.2 轮廓纵向膨胀裂缝提取实验
本文采用的原始数据为核电站安全壳裂缝图像,核电站安全壳裂缝图像为大数据量影像,图幅为7 360像素×4 912像素,图像上裂缝极其细微,噪声密集,污迹、剥落等干扰信息较多,裂缝提取难度较大。为验证轮廓纵向膨胀去噪算法的优越性,本文选取150张核壳影像进行实验,并对比了不同算法的去噪率、裂缝正检率和误检率。去噪算法实验效果如图 5所示,不同算法的去噪率、裂缝正检率和误检率对比如表 1所示。
 |
| 图 5 轮廓纵向膨胀去噪 Figure 5 Contour Longitudinal Expansion Denoising |
| 表 1 轮廓纵向膨胀去噪与经典算法效率对比/% Table 1 Comparison of Contour Longitudinal Expansion Denoising and Classic Algorithms/% |
 |
由实验对比效果可知, 针对核安全壳裂缝图像, 轮廓纵向膨胀去噪算法能很好地滤除大量噪声和非目标的干扰信息,但仍有少量非目标点群遗留。
3 结束语本文利用数字图像处理技术,通过基于轮廓纵向膨胀的核安全壳裂缝提取算法,分割背景,滤除噪声,排除干扰信息,完整提取裂缝点群,利用方向小波裂缝提取算法分割背景并提取裂缝基础信息;提出了轮廓纵向膨胀去噪算法,并融合裂缝轮廓的多形态特征形成裂缝判断置信度,保留绝大部分裂缝点群的同时滤除大量噪声,正确地提取裂缝。但仍有少量的非目标点群在形态上与裂缝相似,或与裂缝相距很近,不可避免地遗留下来,对此仍需做进一步研究。
| [1] | 张祖勋. 数字摄影测量与计算机视觉[J]. 武汉大学学报·信息科学版, 2004, 29(12): 1 035–1 039 |
| [2] | 初秀民, 王荣本, 储江伟, 等. 基于不变矩特征的沥青路面破损图像识别[J]. 吉林大学学报(工学版), 2003, 33(1): 1–7 |
| [3] | 张雷, 肖梅, 马建, 等. 基于视觉模型的路面裂缝检测算法[J]. 长安大学学报(自然科学版), 2009, 29(5): 21–24 |
| [4] | 闫茂德, 伯绍波, 贺昱曜. 一种基于形态学的路面裂缝图像检测与分析方法[J]. 工程图学学报, 2008, 29(2): 142–147 |
| [5] |
唐磊. 基于图像分析的路面病害自动检测[D]. 南京: 南京理工大学, 2007 |
| [6] |
赵轲. 路面裂缝图像自动识别系统研究[D]. 西安: 长安大学, 2009 |
| [7] | Chambon S, Subirats P, Dumoulin J. Introduction of a Wavelet Transform Based on 2D Matched Filter in a Markov Random Field for Fine Structure Extraction: Application on Road Crack Detection[C]. IS & T/SPIE Electronic Imaging, International Society for Optics and Photonics, San Jose, USA, 2009 |
| [8] | Salman M, Mathavan S, Kamal K, et al. Pavement Crack Detection Using the Gabor Filter[C]. The 16th International IEEE Conference on ITSC, The Hague, Netherlands, 2013 |
| [9] | Oliveira H, Correia P L. Automatic Road Crack Detection and Characterization[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(1): 155–168 DOI: 10.1109/TITS.2012.2208630 |
| [10] | Haiyan G. Iterative Tensor Voting for Pavement Crack Extraction Using Mobile Laser Scanning Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1 527–1 537 DOI: 10.1109/TGRS.2014.2344714 |
| [11] | Mordohai P. Tensor Voting:A Perceptual Organization Approach to Computer Vision and Machine Learning[M]. New York: Morgan & Claypool Publishers, 2006 |
| [12] | Abdel-Qader L, Abudayyeh O, Kelly M E. Analysis of Edge Detection Techniques for Crack Identification in Bridges[J]. Journal of Computing in Civil Engineering, 2003, 17(4): 255–263 DOI: 10.1061/(ASCE)0887-3801(2003)17:4(255) |
| [13] | Zhang P, Li H. Recognition of Pavement Surface Crack[C]. International Conference on Natural Computation, Yantai, China, 2010 |
| [14] | 王科俊, 熊新炎, 任桢. 高效均值滤波算法[J]. 计算机应用研究, 2010, 27(2): 434–438 |
| [15] |
李玲. 数字图像点特征及边缘特征提取方法的研究与实现[D]. 西安: 西安科技大学, 2012 |
| [16] |
郝彬彬. 偏微分方程和小波在图像处理中的建模理论及应用[D]. 西安: 西安电子科技大学, 2009 |
| [17] |
许晓丽. 基于聚类分析的图像分割算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012 |
| [18] |
汪岳. 基于边缘检测经典算法的改进研究与实现[D]. 合肥: 安徽大学, 2012 |
| [19] | 葛雯, 高立群, 石振刚. 一种基于小波提升变换的多尺度边缘提取算法[J]. 东北大学学报(自然科学版), 2007, 28(4): 473–476 |
| [20] |
赵瑞珍. 小波理论及其在图像、信号处理中的算法研究[D]. 西安: 西安电子科技大学, 2001 |
 2018, Vol. 43
2018, Vol. 43

