| 自适应显示环境可视化表达的线要素图形化简 |
众源、开放环境下的VGI (志愿者地理信息) 数据是由大量非专业人员志愿获取并通过互联网向大众提供的一种开放型地理信息数据[1, 2]。具有现势性高、信息丰富、数据量大等优点,是地理信息领域一种重要的数据来源[3, 4]。VGI信息的可视化是当前移动互联环境下的一个重要课题,VGI线要素数据的可视化目前面临着以下问题:①元数据信息缺失,数据量纲、比例尺等元信息的缺失致使制图时无法设置适当的比例尺[5]; ②数据冗余,线划矢量点表达密集过量,导致显示缓慢、效率低下; ③地图显示环境多样化,包括有不同分辨率和尺寸大小的PC电脑、智能手机、平板电脑等设备。这些问题严重影响VGI线划要素的表达效果,如何根据外部因素适时地改变可视化策略,达到软件设计上的设备无关性[6],动态地对线划要素简化输出,是一个重要的问题。
针对上述VGI数据冗余,如何处理小尺度空间与大数据表达的问题[7],相关学者结合传统尺度变换与互联网在线环境提出面向自发地理信息数据的在线式综合策略[8, 9],即通过实时综合输出相应比例尺的表达数据,具体方法是:首先对数据进行层次结构化处理,其次,客户端按显示比例尺进行实时综合操作。该方法依赖于数据的比例尺信息进行多尺度表达,对于一些元数据信息缺失的无量纲、无比例尺数据,该方法并不适用,需要对无量纲数据进行比例尺等级匹配,才能实现数据的实时在线综合与多尺度表达。另外,传统的地图自适应可视化研究着重于从用户模型构建、用户认知、用户操作处理方面[10],对于硬件设备多样化的自适应研究较少。
基于上述分析,本文提出了自适应显示窗口环境动态化简线要素的方法解决上述问题。算法的基本思想如下:①建立归一化的自我参考系,对数据统一进行坐标系映射处理;②获取地图显示设备的尺寸大小与屏幕分辨率,并考虑屏幕缩放的尺度变换,实时动态地确定曲线化简参量阈值;③基于上述参量控制对原始数据进行化简,将化简后的点串映射到设备屏幕上进行绘制。该方法的最终目的是实现不论何种数据量纲、大小范围的坐标点串表达的线划要素,在特定的显示窗口环境下都能最佳地展示其可视化效果,达到自适应制图目标。
1 自适应显示环境线化简策略电子地图要实现自适应用户需求产生最佳的空间信息表达效果,就必然具有动态性和交互性[6, 11]:动态性产生不同的电子地图表达,交互性实现用户定制信息。因此要实现自适应地化简线要素,就要根据自适应触发条件动态地对线要素进行简化表达。本文将VGI环境下自适应线化简的触发条件划分为3种:①线划数据质量。VGI数据具有自发性、无序性、非规范性,元数据的不同以及缺失影响着制图比例尺的设置、线要素矢量点的化简参量以及可视化的效率。如图 1(a)、1(b)所示的分别是无量纲与无比例尺的数据。②地图显示环境。地图的显示环境是决定地图视觉感受的重要因素,不同设备的屏幕大小、像素大小、分辨率、CPU处理能力等因素直接决定着设备承载内容的数量与表达细节的能力,从而影响地图的最小视觉辨析与地图要素载负。如图 2所示,同一现状数据在安卓手机和平板电脑上显示具有明显差异。③用户操作。用户的放大、缩小、漫游等操作都会影响地图的位置、比例尺、范围以及要素的密度、数量。图 3表示用户缩放操作对地图可视化效果的影响。
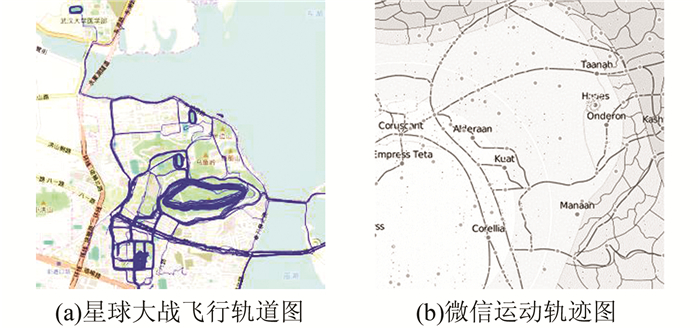 |
| 图 1 VGI用户上传数据 Figure 1 Data by VGI Users |
 |
| 图 2 同一数据在不同设备上的显示差异 Figure 2 Data Shows in Different Devices |
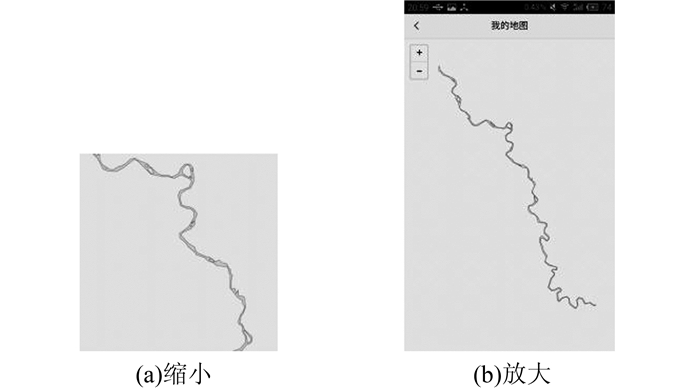 |
| 图 3 用户操作引起地图可视化效果的变化 Figure 3 Visualization Effect Changed by User Actions |
线要素化简的目的是在保持线要素的弯曲特征和复杂程度的前提下,尽量减少线要素的存储量。它是一个依托于化简控制参量,基于某种规则对原始点进行选取或删除的过程。综上所述,自适应显示环境线要素化简可以认为是根据自适应触发条件动态确定线化简控制参量的过程,如图 4所示。自适应线要素化简的过程可以简单地由下面两个公式来表示:
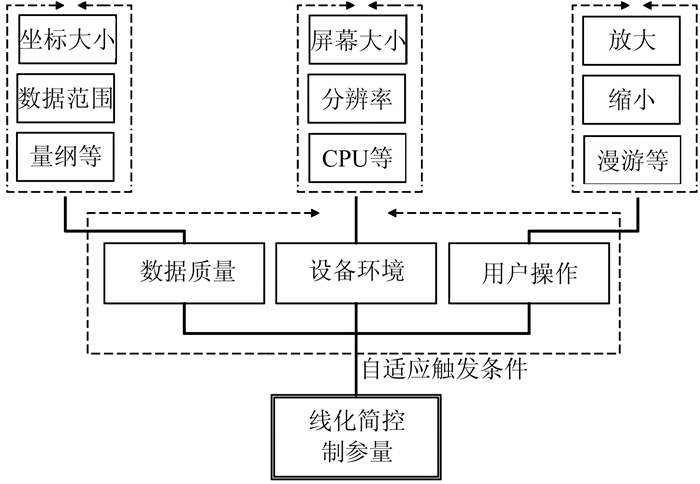 |
| 图 4 自适应线化简 Figure 4 Adaptive Line Simplification |
| $ y = {f_1}\left( s \right) $ | (1) |
| $ s = {f_2}\left( {{x_1}, {x_2}, {x_3}} \right) $ | (2) |
式中,y是最终化简结果;s为化简控制参量;f1为化简规则;x1、x2、x3为自适应触发条件;f2为触发条件对控制参量的作用函数。
2 自适应显示环境线化简方法研究本文的研究是从数据驱动和设备驱动两方面实现线要素的自适应化简。对于不同的数据,面对不同的设备环境,实现动态实时地调整要素的输出表达,最终实现线划要素“好”的显示,即线划光滑自然,既没有马赛克和大的转折,也没有密集的冗余点[12, 13]。下面重点讨论自适应显示环境线要素化简算法的办法步骤。
2.1 坐标系统归一化坐标归一化是将质量参差不齐、量纲不同或者没有量纲的坐标点串映射到自定义的坐标范围内,并保持其线性比例关系,也是对数据进行预处理尺度变换的过程,把不同坐标格式、量纲单位的数据统一成自定义的标准,为之后的自适应化简提供统一的标准数据接口,该过程从最终的化简效果出发,以统一的度量单位与视觉标准对线性要素坐标计算处理。见图 5,本文自定义一个1 000×1 000大小的归一化坐标系:①对数据范围求外接矩形,并获取外接矩形左下角点坐标 (x0, y0) 和外接矩形的宽W、高H;②计算坐标转换系数:m=1 000/max (W, H);③得出坐标转换公式为:xnew=m·(x-x0) ynew=m·(y-y0)。
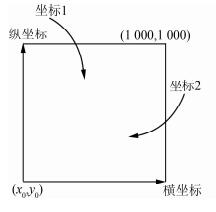 |
| 图 5 坐标归一化示意图 Figure 5 Normalized Coordinate System |
2.2 获取窗口环境信息
读图环境与地图视觉感受息息相关,读图环境的改变必然引起地图视觉效果的变化,对于电子地图来说,电子设备的屏幕大小与分辨率是主要的影响因素,前者影响地图的负载量,后者直接决定最小的像素点距[14, 15]。图 6表示数据坐标与显示设备坐标的映射关系,图 7表示设备分辨率大小对细节显示的影响。此外,地图视觉感受和符号显示的计量单位发生了变化,传统的纸质地图符号设计标准已经不能满足电子地图用户感受与认知的需求,若继续沿用纸质地图的符号设计标准,会导致符号化效果粗糙、比例失调、锯齿状严重等问题,本文通过采用以像素为基本单位将纸质地图线要素化简的视觉阈值单位由mm换算到像素, 换算公式为:
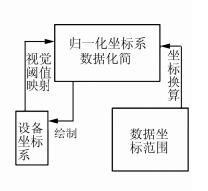 |
| 图 6 数据坐标与设备间的映射关系 Figure 6 Mapping Relation Between Data Coordinate and Devices |
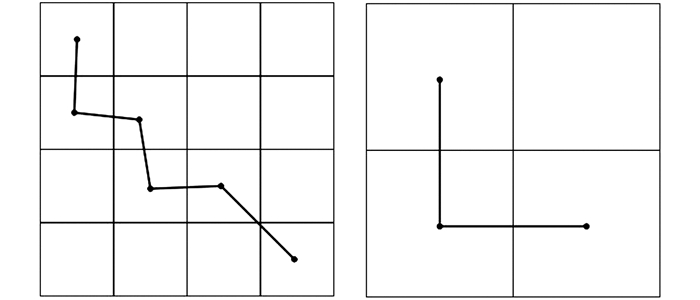 |
| 图 7 分辨率大小对要素细节表达的影响 Figure 7 Effect of Device Resolution on Details Presentation |
| $ \left[{s \cdot {\text{dpi/25}}{\text{.4}}} \right] + 1\;\;\left( {1{\text{英寸 = 24}}{\text{.5}}\;{\text{mm}}} \right) $ | (3) |
综上所述,可以自动获取设备屏幕大小和屏幕分辨率,首先计算出屏幕物理坐标系与归一化坐标系统之间参考系转换系数r1。r1的计算公式为:
| $ {r_1} = 1\;000/\left( {{\text{max}}\left( {H, W} \right) \cdot {\text{dpi}}} \right) $ | (4) |
式中,H、W、dpi分别代表设备的高、宽和分辨率。其次是将地图认知的视觉阈值单位换算成屏幕像素单位,再映射到归一坐标系下,其计算公式为:
| $ {r_1} \cdot \left( {\left[{s \cdot {\text{dpi/25}}{\text{.4}}} \right] + 1} \right) $ | (5) |
地图用户的操作会实时地改变地图视窗的状态,屏幕进行放大缩小时,地图比例尺随之放大缩小,地图要素表现得更加精细或者粗略;屏幕进行漫游操作时,地图的范围与中心点会发生变化,窗口中所表达的坐标范围也随之变化。因此用户进行地图操作时需要:①重新计算视窗范围并对原始数据进行裁切; ②计算出屏幕的缩放系数r2,这是确定线要素化简控制参量的关键一步。通常纸质地图进行线要素化简时,会以最小视觉辨析距离乘以比例尺的倒数作为化简参量,这种关系在电子地图缩放时仍然适用。
依据上述3个步骤得出参考系转换系数、屏幕分辨率和屏幕缩放系数,并根据地图综合的一般规律,计算出线要素化简的控制参量,因此可以把上文提到的线化简模型扩展如下:
| $ \begin{gathered} y = {f_1}\left[{1\;000/\left( {{\text{max}}\left( {H, W} \right) \cdot {\text{dpi}}} \right.} \right] \cdot \hfill \\ \left. {\;\;\;\;\;\;\;\;{r_2} \cdot \left( {\left[{s \cdot \frac{{{\text{dpi}}}}{{{\text{25}}{\text{.4}}}}} \right] + 1} \right) \cdot {r_3}} \right) \hfill \\ \end{gathered} $ | (6) |
式中,y为简化结果;f1为化简规则;H、W是设备的高、宽;r1是参考系转换系数;r2是屏幕缩放系数;s为人眼辨析最小距离,通常情况下取0.1 mm;dpi为屏幕分辨率;r3为其他因素决定的影响因子。
2.4 曲线化简算法本文采用最常用的化简算法Douglas-Peucker算法作为自适应化简的基础算法,算法的基本思路是:对每一条曲线的首末点虚连一条直线, 求所有点与直线的距离, 并找出最大距离值dmax, 用dmax与限差D相比,若dmax < D, 这条曲线上的中间点全部舍去; 若dmax≥D, 保留dmax对应的坐标点, 并以该点为界把曲线分为两部分, 对这两部分重复使用该方法。其中dmax根据上文所述的式 (6) 计算来确定。
2.5 客户端与服务器架构考虑到设备的多样性与设备处理能力的差别,曲线的自适应综合在架构设计上可以分为两种:①客户端收集设备信息和用户的操作上传给后台服务器,后台服务器进行综合处理之后,把结果如切片等返回给客户端,客户端给予结果展示。这种客户端-服务器架构将用户信息与线化简运算分离,只需要在客户端方面进行自适应信息的获取并上传服务器,服务器端可以继续沿用传统的线化简算法,这种架构方式适合大数据量、复杂性较高的综合处理,能大幅度减轻客户端负担,而且运行速度较快;②设备、用户操作信息的收集和线要素的综合化简都在客户端进行,适宜于较小数据量的处理,这种架构对设备的处理能力有一定要求,它的优点在于要素在客户端处理并绘制,具有矢量特征,并能实现离线处理与无级缩放。
2.6 化简结果评价如上文所述,该算法的目的是实现线要素的自适应显示环境化简并实现“好”的显示。其中“好”的显示体现在如下两点:①化简前后有明显的数据压缩,有较高的数据压缩比,数据压缩比可由化简前后数据点数比计算得知;②保证化简后的数据精度缺失在肉眼的可分辨范围内,可视化效果没有较多的重复冗余点,也没有明显的锯齿状。
本文采用最小二乘拟合方法评价化简前后的数据精度,计算公式如下:
| $ {\alpha ^2} = \left( {\sum {\Delta {x^2}} } \right)/n $ | (7) |
式中,α2为平均精度缺失值;Δx2是化简后曲线上的点距离原曲线的最短距离平方 (以屏幕像素值为单位);n是化简后的曲线点数。如果化简前后数据有较高的压缩比,并且化简后曲线的平均精度缺失值小于人眼可辨识的屏幕像素值,可以认为是“好”的化简。
3 实验与讨论基于上述方法模型,本研究采用跨平台开发语言HTML5/JavaScript以及跨平台开发工具Phonegap,开发了自适应显示环境曲线化简实验系统。实验数据采用的是topoJson格式的单线河流数据,数据来源于Natural Earth,原始数据总共有10 607个点。实验平台是个人电脑和安卓智能手机,作为线要素化简的不同显示环境,设备具体信息详见表 1。实验流程如图 8所示。
| 表 1 自适应显示环境线化简结果 Table 1 Results of Adaptive Line Simplification |
 |
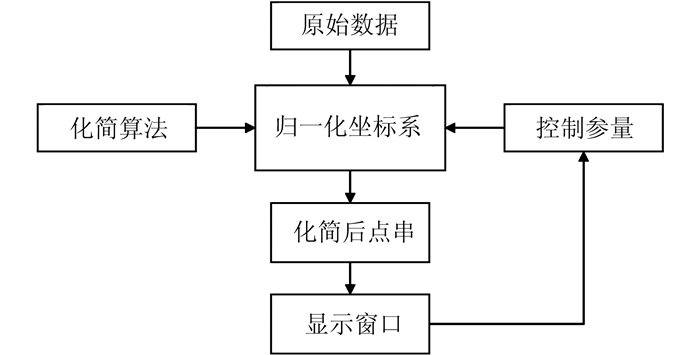 |
| 图 8 实验流程图 Figure 8 Flow Chart of Experiment |
利用本文所述的自适应显示环境线化简算法对河流数据进行动态化简,结果如表 1所示。图 9表示的是原始数据分别在个人电脑和安卓手机中显示的效果,其中设备屏幕坐标系与归一化坐标系之间的参考系转换系数r1分别为100/168、100/256。图 10表示的是应用本文所述模型对矢量线划数据进行自适应动态化简效果对比图。其中, r1表示设备屏幕坐标系与归一化坐标系之间的参考系转换系数;r2表示地图的缩放系数。
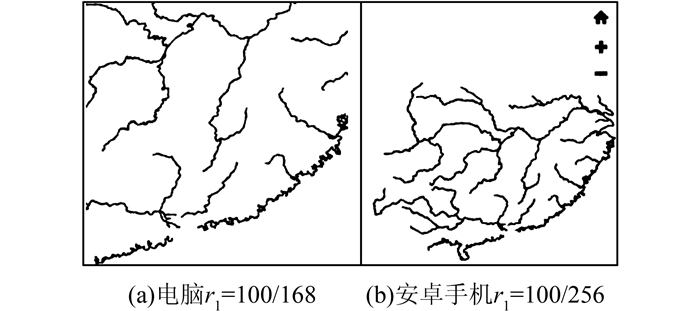 |
| 图 9 原始数据在不同设备下显示效果对比 Figure 9 Raw Data Shows in Different Devices |
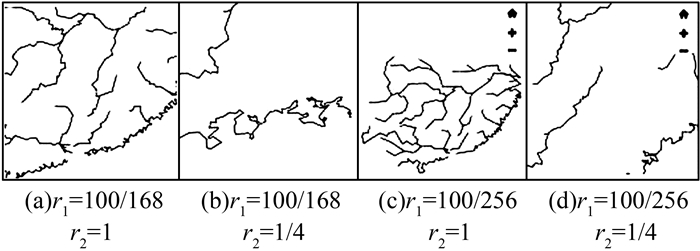 |
| 图 10 自适应显示环境动态线要素化简效果对比 Figure 10 Renderings of Adaptive Line Simplification |
图 9是未经过化简的原始线要素数据,不论在电脑还是在手机上显示都出现了数据点冗余、线划密集的问题。由表 1和图 10可知,在不同的显示环境下,自适应化简算法对曲线做出了不同程度的化简,手机上无缩放的条件下化简比最高,达到了98.60%;电脑上放大2级时化简比最低,也达到了69.90%;并且化简后的数据缺失值都小于可见设备像素值。从实验结果来看:①原始数据得到了有效的化简,并且化简前后数据精度缺失在可接受范围之内;②在不同的显示条件下,线化简的控制参量是实时动态的;③最终的化简结果是由显示窗口条件与地图缩放等级决定的;④可视化效果既没有冗余的重复点,也没有明显的锯齿状。从整体效果上看,该方法实现了根据显示设备自适应化简、根据用户操作动态化简的目的。
4 结束语本文针对众源、VGI数据与地图显示环境多样性的问题,提出了自适应显示窗口环境线化简的算法模型。从数据驱动与显示环境驱动角度提出自适应动态线要素化简的策略,对不同的数据进行归一化处理,根据不同的显示环境自适应地计算化简控制参量,达到动态自动化简的目的。实验表明,该方法能针对不同的环境与数据源,根据不同的用户操作,实时动态地对矢量线性数据进行有效的线化简,数据压缩量明显,显示速度快,有效解决数据冗余、堆叠、显示缓慢等问题。
进一步扩展研究是:把该方法推广到更复杂的多边形综合上,如多边形合并、删除等更多操作,完成完整要素的地图自适应显示环境的可视化;讨论更多的自适应地图综合与可视化策略,实现更智能化的自动综合。
| [1] | Goodchild M F. Citizens as Sensors: the World of Volunteered Geography[J]. GeoJournal, 2007, 69(4): 211–221. DOI: 10.1007/s10708-007-9111-y |
| [2] | Howe J. The Rise of Crowdsourcing[J]. Wired Magazine, 2006, 14(6): 1–4. |
| [3] | 艾廷华. 大数据驱动下的地图学发展[J]. 测绘地理信息, 2016, 41(2): 1–7. |
| [4] | 李德仁, 邵振峰. 论新地理信息时代[J]. 中国科学:信息科学, 2009, 39(6): 579–587. |
| [5] | Flanagin A J, Metzger M J. The Credibility of Volunteered Geographic Information[J]. GeoJournal, 2008, 72(3/4): 137–148. |
| [6] | 王洪, 艾廷华, 祝国瑞. 电子地图可视化中的自适应策略[J]. 武汉大学学报·信息科学版, 2004, 29(6): 525–528. |
| [7] | Huang H, Gartner G. A Technical Survey on Decluttering of Icons in Online Map-Based Mashups[C]. Online Maps with APIs and WebServices. Berlin, Heidelberg: Springer, 2012 |
| [8] | 杨敏, 艾廷华, 卢威, 等. 自发地理信息兴趣点数据在线综合与多尺度可视化方法[J]. 测绘学报, 2015, 44(2): 228–234. |
| [9] | Weibel R, Burghardt D. Generalization, On-the-fly[C]. Encyclopedia of GIS. US: Springer, 2008 |
| [10] | Harrie L. Using Simultaneous Graphic Generalisation in a System for Real-Time Maps[C]. ICA Workshop on Generalisation and Multiple Representation, Leicester, 2004 |
| [11] | 陈毓芬, 陈永华. 地图视觉感受理论在电子地图设计中的应用[J]. 测绘学院学报, 1999, 16(3): 218–221. |
| [12] | Shahriari N, Tao V. Minimising Positional Errors in Line Simplification Using Adaptive Tolerance Values[C]. Advances in Spatial Data Handling. Berlin, Heidelberg: Springer, 2002 |
| [13] | Reichenbacher T. Adaptive Concepts for a Mobile Cartography[J]. Journal of Geographical Sciences, 2001, 11(1): 43–53. DOI: 10.1007/BF02837375 |
| [14] | Rie L, Sarjakoski L T, Lehto L. A Variable-scale Map for Small-display Cartography[J]. International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences, 2002, 34(4): 237–242. |
| [15] | Chenbacher T. Mobile Cartography: Adaptive Visualisation of Geographic Information on Mobile Devices[M]. München: Verlag Dr. Hut,, 2004. |
 2017, Vol. 42
2017, Vol. 42

