| 改进多尺度Retinex增强算法的遥感影像不均匀性校正研究 |
2. 河北工程大学矿业与测绘工程学院,河北 邯郸, 056038;
3. 中国矿业大学(北京)地球科学与测绘工程学院,北京, 100083
2. School of Mining and Geomatics Engineering, Hebei University of Engineering, Handan 056038, China;
3. College of Geoscience and Surveying Engineering, China University of Mining and Technology (Beijing), Beijing 100083, China
在遥感影像的获取或拼接镶嵌过程中,由于光照、天气、空气质量、传感器自身性能、不同的获取时间等因素,遥感影像常常会存在亮度、色调以及反差分布不均匀现象,严重降低遥感影像质量,增加了影像判读和信息提取的难度[1],给后续的影像处理和应用带来困难。为了获得高质量影像信息,校正处理遥感影像不均匀性是遥感影像处理中重要内容。
现有的遥感影像不均匀性校正方法主要包括直方图均衡法[2]、同态滤波法[3]、Mask匀光法[4]、Retinex匀光法[5-7]、基于小波变换的影像增强方法[8]以及基于颜色空间的匀光方法[9]等。直方图均衡化是通过重新分配影像像素值增加影像对比度,适用于背景和前景太亮或者太暗的影像,但经过直方图均衡化变换后的影像灰度级减少,导致细节丢失,在直方图有高峰的影像中,还会出现对比度不自然的过分增强[10]。同态滤波是一种基于频率域的算法模型,通过滤波函数,突出高频削弱低频, 有效增强对比度较低的亮度不均匀遥感影像,但是对彩色影像的不均匀性处理效果较差。Mask匀光算法模型的关键在于利用高斯模糊来获取背景影像,适当尺度下得到的背景影像能很好地模拟影像的亮度分布,达到良好的影像不均匀校正效果,但是在模糊的过程中,会导致局部细节丢失和色彩失真,降低影像清晰度,并且随着高斯模糊尺度的增大, 运算量会成比例增加。
基于单尺度Retinex影像增强方法以及在此基础上发展的多尺度Retinex算法和带彩色恢复多尺度Retinex算法等改进算法[11],从人类视觉特性角度出发,在保证影像整体均匀的同时,提高影像的亮度和对比度,增强影像细节,提高清晰度,使影像更加符合人眼视觉感受,但这类算法会导致影像出现不同程度的颜色失真。基于小波变换的影像增强方法处理后的影像细节清晰、层次感强,提高了影像质量,但影像对比度增强不明显,而且算法计算量较大,运行较慢。基于颜色空间的影像增强方法是将遥感影像从红绿蓝(red green blue, RGB)空间转换到色调、亮度、饱和度(hue intersity saturation, HIS)、色调、饱和度、亮度(hue saturation value, HSV)等颜色空间,分析各分量之间的相关性,根据影像的不同需求对各分量进行调整,达到影像不均匀性校正的目的, 具有很强的适应性,但是各个分量之间的相关性较为复杂,容易产生相互干扰。
本文采用基于均值和方差的Retinex算法对色调、亮度不均匀遥感影像进行不均匀性校正处理,提高影像的均匀性,避免颜色失真,增大细节反差,提高影像清晰度。
1 Retinex算法基本理论1) 单尺度Retinex算法(single-scale Retinex,SSR)是在中心/环绕Retinex的基础上发展起来的一种人类视觉亮度和颜色感知的计算理论模型,其算法原理是将一幅影像F(x, y)看作是照度分量I(x, y)和反射分量R(x, y)的乘积。
I(x, y)反映影像的亮度分布, R(x, y)反映影像中物体的特征信息。Retinex算法就是通过降低照度分量,增加反射分量,从而反映出物体的实际特征信息,达到匀光匀色的目的。一般处理过程由原始遥感影像进行不均匀照度分布估计,分离出原始影像的照度估计量,得到匀光影像。
单尺度Retinex算法公式为:
| $ \begin{align} & {{r}_{i}}\left( x, y \right)=\text{lg}\left[ {{R}_{i}}\left( x, y \right) \right]=\text{lg}\left[ {{F}_{i}}~\left( x, y \right) \right]- \\ & \ \ \ \ \ \ \ \ \text{ }\!\!~\!\!\text{ lg}\left[ {{F}_{i}}~\left( x, y \right)*{{H}_{i}}\left( x, y \right) \right] \\ \end{align} $ | (1) |
式中, ri(x, y)为对数域中的估计反射分量,对其取指数得到不均匀校正后的影像;F (x, y)为原始遥感影像;*表示卷积运算;i表示遥感影像第i个波段;H(x, y)为滤波函数,通常选用高斯低通滤波函数,表达式为:
| $ H\left( x, y \right)=p\times \text{exp}~\left( -\frac{\text{ }{{x}^{2}}+{{y}^{2}}}{{{\sigma }^{2}}} \right)~ $ | (2) |
式中, σ为高斯函数尺度参数,即高斯函数标准差;p为归一化参数,满足条件
2) 多尺度Retinex算法(multi scale Retinex,MSR)是对单尺度Retinex算法的综合,将各不同尺度下单尺度Retinex算法结果加权平均,数学表达式为:
| $ {{m}_{in}}\left( x, y \right)=\sum\limits_{i=1}^{n}{{{w}_{n}}{{r}_{in}}~\left( x, y \right)} $ | (3) |
式中, min(x, y)是MSR第i个波段的输出影像,n是第n个尺度;wn是第n个尺度对应SSR输出结果的权重, 且
3) 色彩恢复的多尺度Retinex增强算法(multi scale Retinex with color restoration, MSRCR)是在MSR基础上引入色彩恢复因子C,在增强影像的同时,避免颜色失真,其模型原理是通过原影像各波段在不同像元位置中的比例关系对MSRCR输出影像进行修正,避免因为Retinex算法导致颜色失真。其数学表达式为:
| $ {{C}_{i}}\left( x, y \right)=\text{lg}\left( \frac{{{T}_{i}}\left( x, y \right)}{\sum\limits_{i=1}^{k}{{{T}_{i}}\left( x, y \right)}}~ \right) $ | (4) |
式中, Ci(x, y)是影像第i个波段在(x, y)像元上的色彩恢复系数; Ti(x, y)是影像第i个波段在(x, y)上的像元值; k是影像波段总数。MSRCR算法是基于原始影像色彩进行恢复,对于原本色彩不均匀,或颜色信息已被严重破坏的影像处理效果不好[13]。
2 基于均值和方差的Retinex算法以上3种算法虽然都能较好地解决亮度不均匀分布,但SSR和MSR都会出现不同程度的颜色失真,MSRCR对于色彩不均匀的原始影像没有作用,而基于均值和方差的Retinex算法则能较好地解决色彩失真问题。
基于均值和方差的Retinex算法通常应用于普通数字图像的光照增强,而对于遥感影像色调、亮度不均匀分布的校正处理也有较好效果。该算法主要是在对MSR结果影像的量化方式上,引入结果影像各波段均值和方差,并通过控制影像动态参数来实现无色偏的调节过程,达到对影像色调、亮度不均匀分布校正的目的。
计算出MSR结果影像各波段最大值和最小值:
| $ \left\{ \begin{align} & {{i}_{\text{min}}}={{i}_{m}}-D\times {{V}_{i}} \\ & {{i}_{\text{max}}}={{i}_{m}}+D\times {{V}_{i}} \\ \end{align} \right. $ | (5) |
式中, imax和imin分别为MSR结果影像第i波段的最大值和最小值; im是第i波段均值; D为动态参数,本文选择D=2;Vi是第i波段方差。为了增加影像整体反差,对其作线性灰度变换,对MSR结果影像每一个值Value进行线性映射,将像元值拉伸到[0-255]范围为:
| $ {{r}_{i}}\left( x, y \right)=({{i}_{\text{Value}}}-{{i}_{\text{min}}})/({{i}_{\text{max}}}-{{i}_{\text{min}}})\times (255-0) $ | (6) |
在处理过程中,对于像元值溢出的像元,进行溢出处理为:
| $ \left\{ \begin{align} & {{r}_{i}}~\left( x, y \right)=255, {{r}_{i}}~\left( x, y \right)>255 \\ & {{r}_{i}}~\left( x, y \right)=0, {{r}_{i}}~\left( x, y \right) <0~ \\ \end{align} \right. $ | (7) |
基于均值和方差的Retinex算法,在多尺度Retinex结果影像基础上改善处理后的影像色偏,达到了较好的视觉效果。
3 实验与分析两组实验所用影像为两幅拼接后的高分一号遥感影像,大小分别为538像素×528像素和536像素×521像素。第1幅影像左侧色调明显偏白,亮度也较高;第2幅影像右侧偏暗,亮度偏低。两幅拼接影像都出现明显的亮度、色调分布不均匀现象,视觉效果较差,不利于影像的判读和信息提取。对于不均匀性校正处理后的影像主要从视觉效果和定量指标进行评价,由于遥感影像成像复杂,影响因素众多,定量评价结果与人主观视觉感受可能有很大出入[14]。因此,对于不均匀光照遥感影像质量评价应以主观评价为主结合定量评价结果进行综合评价。
1) 视觉效果评价。实验分别用SSR、MSR、MSRCR和基于均值和方差的Retinex算法对两组影像进行不均匀性校正处理,获得结果影像如图 1所示。
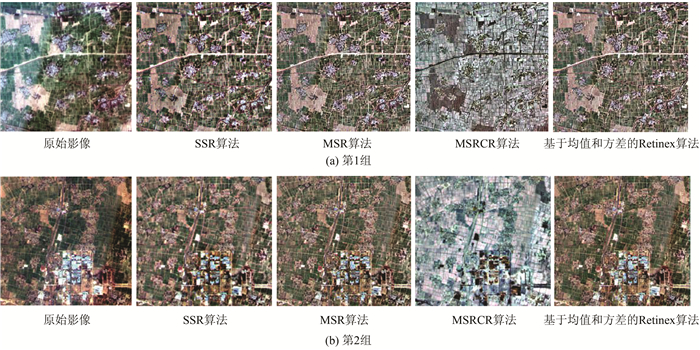 |
| 图 1 不均匀影像处理结果 Fig.1 Uneven Image Processing Results |
对比分析两组实验影像,从视觉角度上看,原始拼接影像存在严重的色调和亮度差异,影响影像质量,不利于判读;SSR算法得到的影像比较模糊,色调、亮度差异仍较大;由于原始影像色彩并不均匀,基于原始影像进行的MSRCR色彩恢复后的影像色调偏差反而更大,没有达到理想的效果;MSR和基于均值和方差的Retinex算法效果较好,亮度、色调比较均匀,影像清晰,细节信息丰富,目视效果良好。
2) 实验遥感影像质量的定量评价。该评价主要从平均梯度和标准差来衡量,平均梯度反映图像对微小细节反差表达的能力,平均梯度越大表明影像越清晰,目视效果越好,标准差反应各个像元灰度相对于灰度平均值的离散情况,标准差越小表明影像亮度、色调越均匀[15]。实验分别将两组原始影像和结果影像红、绿、蓝3个波段的平均梯度和标准差进行对比,结果如表 1所示。
| 表 1 影像3个波段的处理结果 Tab.1 Processing Results of the Three Bands of Images |
 |
从表 1的两组实验数据来看,SSR、MSR、MSRCR与基于均值和方差的Retinex算法处理后的影像平均梯度相较于原始影像都有很大程度提高,其中MSR平均梯度最高,基于均值和方差的Retinex算法较低,表明影像经过校正后更清晰,对比度增强,细节也更突出,目视效果更好;MSR结果影像最清晰,基于均值和方差的Retinex算法结果影像清晰度较差。
由于Retinex算法本身有增强对比度的效果,所以4种算法处理后的影像标准差都会增大,但是从目视效果上看,很大程度上削弱了色调、亮度的异常反差,其中,基于均值和方差的Retinex算法标准差最低,其影像的色调和亮度最均匀,达到了良好的视觉效果。
4 结束语对于存在明显色调、亮度不均匀分布的遥感影像,SSR匀光匀色效果一般,不能很好地解决色调、亮度分布不均匀问题,而且会出现不同程度颜色失真;MSR兼顾不同尺度下SSR处理结果的优势,在保证影像清晰度的同时,基本解决影像色调、亮度反差较大的问题,同时改善SSR中色彩失真的缺憾;MSRCR对于原本色彩不均匀,或颜色信息已被严重破坏的影像效果不好,出现较大色调偏差,视觉上不够理想;基于均值和方差的Retinex算法很大程度上减弱了影像色调、亮度的异常反差,同时增加了影像细节,提高了清晰度。无论从视觉上还是从定量分析评价结果来看,基于均值和方差的Retinex算法相比其他3种算法效果要好。
| [1] |
邵振峰, 白云, 周熙然. 改进多尺度Retinex理论的低照度遥感影像增强方法[J]. 武汉大学学报·信息科学版, 2015, 40(1): 32-39. |
| [2] |
Celik T. Two-Dimensional Histogram Equalization and Contrast Enhancement[J]. Pattern Recognition, 2012, 45(10): 3810-3824. DOI:10.1016/j.patcog.2012.03.019 |
| [3] |
刘毅, 贾旭芬, 田子建. 一种基于同态滤波原理的井下光照不均图像处理方法[J]. 工矿自动化, 2013, 39(1): 9-12. |
| [4] |
王密, 潘俊. 一种数字航空影像的匀光方法[J]. 中国图象图形学报, 2004, 9(6): 744-748. DOI:10.3969/j.issn.1006-8961.2004.06.016 |
| [5] |
李慧芳, 沈焕锋, 张良培, 等. 一种基于变分Retinex的遥感影像不均匀性校正方法[J]. 测绘学报, 2010, 39(6): 585-591. |
| [6] |
张尚伟, 曾平, 罗雪梅, 等. 具有细节补偿和色彩恢复的多尺度Retinex色调映射算法[J]. 西安交通大学学报, 2012, 46(4): 32-37. |
| [7] |
Rahman Z U, Jobson D J, Woodell G A. Retinex Processing for Automatic Image Enhancement[J]. Journal of Electronic Imaging, 2004, 13(1): 100-110. DOI:10.1117/1.1636183 |
| [8] |
Hsung T C, Lun D P K, Ng W W L. Efficient Fringe Image Enhancement Based on Dual-Tree Complex Wavelet Transform[J]. Applied Optics, 2011, 50(21): 3973-3986. DOI:10.1364/AO.50.003973 |
| [9] |
秦绪佳, 王慧玲, 杜轶诚, 等. HSV色彩空间的Retinex结构光图像增强算法[J]. 计算机辅助设计与图形学学报, 2013, 25(4): 488-493. DOI:10.3969/j.issn.1003-9775.2013.04.008 |
| [10] |
Chen S D, Ramli A R. Contrast Enhancement Using Recursive Mean-Separate Histogram Equalization for Scalable Brightness Preservation[J]. IEEE Transactions on Consumer Electronics, 2003, 49(4): 1301-1309. DOI:10.1109/TCE.2003.1261233 |
| [11] |
Jang J H, Kim S D, Ra J B. Enhancement of Optical Remote Sensing Images by Subband-Decomposed Multi-scale Retinex with Hybrid Intensity Transfer Function[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(5): 983-987. DOI:10.1109/LGRS.2011.2146227 |
| [12] |
王龙志, 姚晓天, 孟卓, 等. 基于自适应多尺度Retinex的光学相干层析图像衰减补偿算法[J]. 中国激光, 2013, 40(12): 113-118. |
| [13] |
洪平.基于RETINEX理论的图像去雾研究[D].上海: 上海交通大学, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10248-1013021745.htm
|
| [14] |
张云翔, 于杰. 基于资源三号的DSM自动生成方法与质量控制[J]. 测绘地理信息, 2017, 42(4): 43-46. |
| [15] |
朱述龙, 张振, 朱宝山, 等. 遥感影像亮度和反差分布不均匀性校正算法的效果比较[J]. 遥感学报, 2011, 15(1): 111-122. |
 2019, Vol. 44
2019, Vol. 44

