| 遥感影像像元不确定性对SVM分类结果可靠性影响研究 |
近年来,遥感数据因其高空间分辨率、覆盖范围广、多时相、信息量丰富等特点,被广泛应用于土地利用规划、灾害监测、目标检测等领域,成为处理地理信息问题的主要信息源,但随着遥感技术的发展,遥感数据的不确定性特征严重制约着遥感技术应用的进一步发展,因此遥感数据不确定性研究引起了相关学者的广泛关注[1]。不确定性是客观世界和实体本身所具有的固有属性,它可以反映所获取的数据与真实数据值之间存在的误差大小[2]。遥感数据的不确定性存在于整个数据的生命周期,包括数据获取、传输、处理和信息提取、精度评价等,并且不断传播和积累,最终影响输出成果的精度[3]。目前,在遥感数据不确定性研究中,一方面,有关学者相继利用概率论、模糊数学、灰色理论等方法分别从像元、类别、总体3个方面对遥感影像数据的不确定性进行度量[4]。例如,Foody[5]以概率矢量为基础提出一系列指标来描述像元的不确定性;刘艳芳等[6]提出混合熵模型从像元尺度和类别尺度综合测度遥感分类过程中产生的随机不确定性和模糊不确定性;Jager等[7]以模糊相似性为基础建立了一系列类别不确定性评价指标;吴浩等[8]从像元和类别两个尺度构建多维混合熵模型来评价遥感影像分类过程中的不确定性;李三平[9]以粗糙集理论为基础,采用近似分类精度和近似分类质量度量影像整体的不确定性。另一方面,还有些学者致力于研究遥感信息中不确定性的传递机理,葛咏等[10]结合合成孔径雷达(synthetic aperture radar, SAR)系统提出基于系统机理的误差分析方法,建立信息传递函数,构造不确定性传递模型。
综上所述,国内外众多学者已经从各方面对遥感数据的不确定性进行了研究,并取得了一定的成果,但目前鲜有方法将遥感信息产品结果的可靠性和不确定性结合讨论。为此,本文基于信息论和概率论构建像元不确定性描述指标和量化表达模型,从而对遥感影像像元不确定性进行描述,同时建立影像分类可靠性评价指标体系。在此基础上,利用线性回归建模分析支持向量机(support vector machine, SVM)分类结果可靠性各指标与像元不确定性的相关关系,从而探索遥感影像像元的不确定性对分类可靠性的影响规律,为拓展和深化影像可靠性分类理论和技术提供科学基础与技术储备。
1 研究方法 1.1 影像的像元不确定性度量指标遥感影像数据在获取和传递过程中会产生不确定性,这种不确定性影响最终产品的可靠性。目前已有的像元不确定性度量指标大多只从一个方面度量不确定性,存在一定缺陷。因此,本文综合考虑不确定性产生的原因及特征,从不同方面在像元尺度上构建不确定性度量指标。
1)像元光谱多义性。遥感影像往往包含大量的混合像元,混合像元在一定程度上造成了分类结果的不确定性。本文引入信息熵模型和混合像元光谱分解模型来计算混合像元光谱多义性,以信息熵值来表示不确定性大小。信息熵值越大,表示像元内部光谱信息越复杂,像元光谱多义性越大,像元不确定性越大。其计算公式如下:
| $ H=-\sum\limits_{i}^{n} a_{i} \log _{2} a_{i} $ | (1) |
式中,H为像元信息熵值;n为类别数;ai为利用光谱解混模型得到的像元属于第i类端元的丰度比例。
2)像元灰度差异性。遥感影像像元之间灰度值的变化可以反映影像空间信息的变化,特别是位于边缘的过渡性像元,其灰度值一般与周围像元灰度差异大,这些像元不确定性高。因此,本文利用像元灰度值与邻域像元的灰度差异反映像元不确定性大小,像元灰度值与周围像元灰度值差异性均值越大,表明像元不确定性越大。计算公式如下:
| $ \overline{G_{D}}=\frac{1}{m} \sum\limits_{j=1}^{m}\left|p_{d}-p_{e}\right| $ | (2) |
式中,
3)像元分类信任度。像元本身含有的不确定性使不同分类器对同一像元的分类结果可能存在较大差异,这种不确定性在一定程度上可以通过像元分类信任度反映。本文利用信任函数来计算像元分类信任度[11],首先利用混淆矩阵得到分类器对各个样本类别的识别正确率(局部信任度),然后结合像元属于各类的局部信任度和像元属于各类的后验概率,得到像元属于各类的信任程度。另外,为了降低单一分类算法输出结果的误差,加权综合多个分类器得到的像元属于各个类别的分类信任度,在此基础上通过最大信任度原则,将信任值最大的值作为该像元最终的像元分类信任度。像元分类信任度越大,像元不确定性越小。公式如下:
| $ C_{C}= \\ \max \left(\sum\limits_{1}^{b} w_{b} r_{g 1} p_{g 1}, \sum\limits_{1}^{n} w_{b} r_{g 2} p_{g 2}, \cdots, \sum\limits_{1}^{b} w_{b} r_{g k} p_{g k}\right) $ | (3) |
式中,b表示分类器;wb为分类器b的权重;rgk为像元g属于k类别的局部信任度;pgk为分类器b将像元g分成k类别的后验概率。
1.2 分类结果的可靠性度量影像分类的可靠性指在规定样本和规定分类算法下取得正确、有效、完整的分类结果的能力,它可以很好地表示一个分类器的实用性。目前,史文中等[12]已经从数据、方法、结果3个方面对空间分析可靠性提出一些评价指标,如准确性、完整性、一致性、适用性。但具体到分类可靠性评价仍缺乏相对统一和意义明确的评价指标。本文在此基础上构建分类结果可靠性评价指标,设Ω为要素集合;f为要素类型;Ωtf为实际地面要素f的像元的集合;NΩtf为实际地面要素f的像元的数量;NΩff为分类结果中要素f的数量;NCf为正确分类成f要素的像元数量;Cf为正确分类的f要素集合。
1)正确性是指在分类结果中,正确分类的像元所占全部分类像元的比例,即总体精度,表示为:
| $ {A_O} = 1 - \frac{1}{{\sum_f {\left| {{C_f} - {\mathit{\Omega }_{tf}}} \right|} }} $ | (4) |
2)一致性描述了遥感影像分类结果与实际地面地物分布的一致程度,通常利用Kappa系数(K)来描述。其计算公式为:
| $ K=\frac{p_{o}-p_{c}}{1-p_{c}} $ | (5) |
式中,po表示实际正确分类的比例,即总体分类精度;pc表示预期正确分类的比例。
3)完整度反映了数据集中的实体对象对现实世界中实体描述的完整程度,即分类结果的无遗漏性。计算公式如下:
| $ {I_C} = 1 - \sum_f {\frac{{{N_{{O_f}}}}}{{{N_{{\mathit{\Omega }_{tf}}}}}}} $ | (6) |
式中,NOf表示f要素分类结果中遗漏像元的数量。
4)可靠度描述了分类数据集中实体对象反映实际地面真实情况的比例,它可以反映分类结果的准确性。计算公式如下:
| $ {R_C} = 1 - \sum_f {\frac{{{N_{{O_f}}}}}{{{N_{{\mathit{\Omega }_{ff}}}}}}} $ | (7) |
已有研究表明影像不确定性对分类可靠性存在一定影响,但像元本身存在的不确定性对分类结果可靠性的影响模式和影响规律仍需进一步探究。本文利用一元线性回归分析对像元不确定性和SVM分类结果的可靠性指标进行建模分析,从而得到像元不确定性对SVM分类结果可靠性的影响程度。一元线性回归模型表示如下:
| $ y=\beta_{0}+\beta_{1} x+\varepsilon $ | (8) |
式中,y是因变量,本文指像元g分类结果可靠性指标;x是自变量,本文指像元g综合不确定性;ε是误差项;β0和β1称为模型参数,可以通过最小二乘法估计得到:
| $ \hat{\beta}_{1}=\frac{s \sum\limits_{g=1}^{s} x_{g} y_{g}-\left(\sum\limits_{g=1}^{s} x_{g}\right)\left(\sum\limits_{g=1}^{s} y_{g}\right)}{s \sum\limits_{g=1}^{s} x_{g}^{2}-\left(\sum\limits_{g=1}^{s} x_{g}\right)^{2}} $ | (9) |
| $ \hat{\beta}_{0}=\bar{y}-\hat{\beta}_{1} \bar{x} $ | (10) |
式中,s指像元总数;
R2检验因变量y与自变量x相关性程度,其值越接近1,说明变量之间的线性相关性越强。计算公式如下:
| $ R^{2}=\frac{\left(s \sum x_{g} y_{g}-\sum x_{g} \sum y_{g}\right)^{2}}{\left(s \sum x_{g}^{2}-\left(\sum x_{g}\right)^{2}\right)\left(s \sum y_{g}^{2}-\left(\sum y_{g}\right)^{2}\right)} $ | (11) |
1)研究数据。为了更加准确地分析像元不确定性对SVM分类结果可靠性的影响,本文选取不同区域、不同分辨率的4幅影像进行实验,见图 1。图 1(a)是青海省西宁市地区2016年5月北京二号(BJ2)卫星遥感影像,尺寸为376×312像素,空间分辨率为3.2 m,影像类别包括水体、裸土、草地、林地、建筑;图 1(b)是2015年9月深圳市铁岗水库地区的高分一号(GF1)卫星遥感数据,尺寸为258×229像素,空间分辨率为16 m,影像类别包括水体、裸土、道路、建筑区、林地;图 1(c)是由Landsat 8OLI传感器获得的位于深圳市石岩水库的2016年8月的影像数据,大小为200×200像素,空间分辨率为30 m,影像类别包括水体、裸土、道路、建筑区、林地。图 1(d)是安徽省淮北市地区2014年12月的WorldView2遥感影像,大小为726×894像素,空间分辨率1.2 m,影像类别包括水体、裸土、道路、建筑区、林地、草地、耕地。
 |
| 图 1 原始影像数据 Fig.1 Original Remote Sensing Data |
2)像元综合不确定性度量。将上述各种不确定性指标计算模型分别应用到每个影像上,其中,本文通过平均加权SVM分类法和最大似然法分类得到的像元后验概率计算像元分类信任度。在此基础上,根据式(12)计算像元综合不确定性。本文各指标的权重利用平均加权计算,并将结果归一化到[0, 1],结果如图 2所示。从图 2中可以直观地了解像元不确定性的空间分布,像元越亮表示其不确定性越大。
| $ U_{N}=\sum\limits_{\theta}^{v} w_{\theta} u_{\theta} $ | (12) |
 |
| 图 2 像元不确定性大小分布 Fig.2 Distribution of Pixel Uncertainty |
式中,UN代表综合不确定性;v表示不确定性度量指标个数;uθ表示不确定性指标θ的大小;wθ表示不确定性指标θ的权重。
3)像元不确定性大小与分类可靠性指标回归分析。本文通过回归分析法分析可靠性指标与像元不确定性之间的关系。首先将所得到的像元综合不确定性数据以相同的区间进行划分,然后联合SVM分类器分类的结果图和地面真值图分别计算各个区间的可靠性指标,最后将得到的各个区间可靠性指标和相对应的不确定性指标进行回归建模分析。本文建立的一元线性回归模型中,x代表像元不确定性,y代表对应的分类结果可靠性指标。
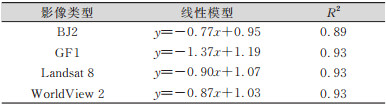
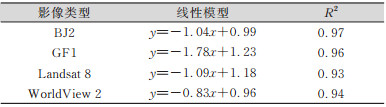
① 正确性和一致性。表 1和表 2分别是根据像元不确定性和分类结果正确性、一致性Kappa系数,利用一元线性回归建立的关系模型。由表 1、表 2可知,4组影像的分类正确性、一致性和像元不确定基本成线性关系,相关性较强,这说明像元不确定性大的区域,其总体分类正确性和分类一致性低。
| 表 1 像元不确定性与分类正确性回归分析 Tab.1 Regression Analysis on Pixel Uncertainty and Classification Correctness |
 |
| 表 2 像元不确定性与分类一致性回归分析 Tab.2 Regression Analysis on Pixel Uncertainty and Classification Consistency |
 |
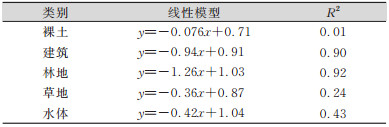
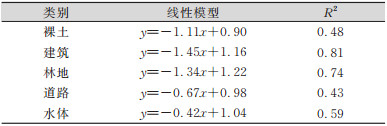
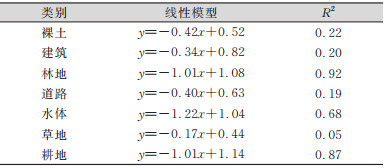
② 完整度。表 3~表 6分别是4组影像数据像元不确定性与分类结果完整性的回归分析结果。4组影像中像元不确定性对各个类别的分类完整度的影响存在明显差异。其中,影像中耕地、林地的分类完整度受不确定性的影响,线性关系较强;水体和道路分类完整度受像元不确定性影响,线性关系稍弱;裸土和草地的分类完整度受像元不确定性影响,且在不同影像中呈现不同变化。这可能与不同影像中地物的空间分布类型和数量有关,比如影像中存在难以区分的地物,如草地和裸土、道路和建筑区等。SVM分类器不易区分这些地物,在分类时,不确定性小的区域中,某种地物可能会被分成另一种地物,从而使得分类结果的可靠性降低。
| 表 3 BJ2影像像元不确定性与完整度回归分析 Tab.3 Regression Analysis on Pixel Uncertainty and Integrity of BJ2 Image |
 |
| 表 4 GF1影像像元不确定性与完整度回归分析 Tab.4 Regression Analysis on Pixel Uncertainty and Integrity of GF1 Image |
 |
| 表 5 Landsat 8影像像元不确定性与完整度回归分析 Tab.5 Regression Analysis on Pixel Uncertainty and Integrity of Landsat 8 Image |
 |
| 表 6 WorldView2影像像元不确定性与完整度回归分析 Tab.6 Regression Analysis on Pixel Uncertainty and Integrity of WorldView2 Image |
 |
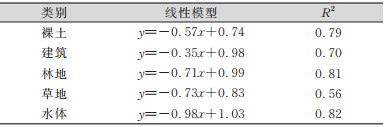
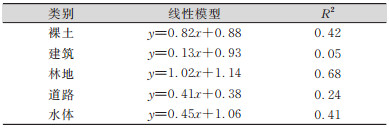
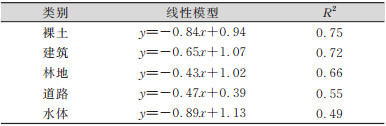
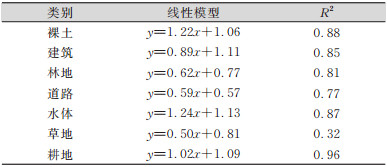
③ 可靠度。表 7~表 10分别是4组影像数据像元不确定性与分类结果可靠度的回归分析结果。分类可靠度受不确定性的影响在不同类别、不同影像中存在明显差异。不同影像中分布连续、完整的地物的分类结果可靠度与其不确定性相关性较强,如林地、耕地、水体;BJ2和WorldView2高分辨率影像像元不确定性对分类可靠度的影响在相同地物类型下一般强于GF1和Landsat 8影像。
| 表 7 BJ2影像像元不确定性与可靠度回归分析 Tab.7 Regression Analysis on Pixel Uncertainty and Reliability of BJ2 Image |
 |
| 表 8 GF1影像像元不确定性与可靠度回归分析 Tab.8 Regression Analysis on Pixel Uncertainty and Reliability of GF1 Image |
 |
| 表 9 Landsat 8影像像元不确定性大小与可靠度回归分析 Tab.9 Regression Analysis on Pixel Uncertainty and Reliability of Landsat 8 Image |
 |
| 表 10 WorldView2影像像元不确定性与可靠度回归分析 Tab.10 Regression Analysis on Pixel Uncertainty and Reliability of WorldView2 Image |
 |
3 结束语
本文基于信息论和概率论,从光谱差异、灰度差异和分类信任度3个方面,在像元尺度上对影像的不确定性信息进行描述,建立像元不确定性的统一量化表征数学模型,然后结合构建的分类可靠性评价指标,利用回归分析建模探索了BJ2、GF1、Landsat 8和WorldView 4幅影像不确定性对SVM分类结果可靠性的影响规律。实验结果表明,本文提出的不确定性评价指标能在一定程度上反映影像像元的不确定性,同时影像像元不确定性对SVM分类的可靠性存在一定影响,像元不确定性越大,分类可靠性相关指标越低。整体上,影像像元的不确定性和分类结果的正确性、一致性呈现明显的线性递减关系,在类别上,影像不确定性对同一地物类型的分类完整度和可靠度在不同分辨率的影像间存在差异。
| [1] |
遥感数据模糊不确定性来源及其处理方法的探讨[J]. 测绘科学, 2008, 33(6): 107-109. DOI:10.3771/j.issn.1009-2307.2008.06.037 |
| [2] |
GIS不确定性框架体系与数据不确定性研究方法[J]. 地理学与国土研究, 2002, 18(4): 1-5. DOI:10.3969/j.issn.1672-0504.2002.04.001 |
| [3] |
遥感与地理信息系统数据的信息量及不确定性[J]. 武汉大学学报·信息科学版, 2006, 31(7): 569-572. |
| [4] |
Ayyub B M, Klir G J. Uncertainty Modeling and Analysis in Engineering and the Sciences[M]. Boca Raton: CRC Press, 2006
|
| [5] |
Foody G M. Approaches for the Production and Evaluation of Fuzzy Land Cover Classifications from Remotely-Sensed Data[J]. International Journal of Remote Sensing, 1996, 17(7): 1 317-1 340. DOI:10.1080/01431169608948706 |
| [6] |
基于混合熵模型的遥感分类不确定性的多尺度评价方法研究[J]. 测绘学报, 2009, 38(1): 82-87. DOI:10.3321/j.issn:1001-1595.2009.01.014 |
| [7] |
Jager G, Benz U. Measures of Classification Accuracy Based on Fuzzy Similarity[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(3): 1 462-1 467. DOI:10.1109/36.843043 |
| [8] |
遥感云分类不确定性的多维混合熵模型评价[J]. 测绘科学, 2016, 41(5): 50-54. |
| [9] |
李三平. 遥感信息不确定性建模及其可视化表达研究[D]. 太原: 山西大学, 2006
|
| [10] |
遥感信息不确定性研究[J]. 遥感学报, 2004, 8(4): 339-348. |
| [11] |
结合SVM与DS证据理论的信息融合分类方法[J]. 计算机工程与应用, 2013, 49(11): 114-117. DOI:10.3778/j.issn.1002-8331.1110-0377 |
| [12] |
可靠性空间分析初探[J]. 武汉大学学报·信息科学版, 2012, 37(8): 883-887. |
 2021, Vol. 46
2021, Vol. 46


