| 地震监测精密水准网中独立环闭合差计算 |
中国综合地球物理场观测——大华北地区项目,主要是对大华北地区的地震水准监测网进行优化改造,进行精密水准测量,为地震预报和科学研究提供准确可靠的观测数据。该水准网涉及6个省份,地域辽阔,由近70个水准环线构成,而如此多的水准环线又由众多的单一水准路线组成,所以施测中不仅要使这些单一水准路线测段不符值、区段不符值符合限差要求,而且要使最终形成的水准网各独立环闭合。作业员在外业用水准仪所测的高差是最原始的数据,其中存在各项误差,在计算环闭合差过程中必须进行相应的高差改正,主要包括:水准标尺长度改正、正常水准面不平行改正、重力异常改正、水准标尺温度改正、固体潮改正、海潮负荷改正。
在地震部门中,一般只考虑前3项的改正:水准标尺长度改正计算δ、正常水准面不平行改正计算ε、重力异常改正计算λ。下面对这3项改正逐一分析、计算。
1 3项改正的具体分析和计算 1.1 水准标尺长度改正实施精密水准测量前后,必须对水准标尺进行标尺长度检定。如测量前后,水准标尺检定长度与其真长的差值不大于±30 μm,则取变化值的均值作为改正量,进行尺长改正;否则水准标尺不应使用,或者观测成果作废[1]。
水准标尺长度改正按公式(1) 计算:
| $\delta =f\cdot h$ | (1) |
其中,h为一测段往测或者返测高差值,单位为m;f为水准标尺改正系数,单位为mm/m。
在某段实测水准线路中,使用蔡司厂生产的NI002A型水准仪、中国珠峰仪器厂生产的一等水准标尺。经检定,测前水准标尺改正系数f1=-0.008 mm/m,测后水准标尺改正系数f2=-0.001 mm/m,则f=(f1+f2)/2=-0.004 mm/m满足要求,假设水准点A到水准点B的往、返测高差为:h往=-6 882.78 mm,h返=+6 882.80 mm,则高差中数h按公式(2) 计算:
| $h=({{h}_{往}}+{{h}_{返}})/2$ | (2) |
可得h=-(6 882.78+6 882.80) /2=-6 882.79 mm,其中h的符号冠以往测符号“-”。
则按式(1) 计算得:δ=-0.004×(-6 882.79) =+0.03 mm。
改正后高差中数为:h+δ=-6 882.79+0.03=-6 882.76 mm。
1.2 正常水准面不平行改正进行水准测量工作时,当水准仪被整平后,水准仪的视准轴应视为水平,即与仪器等高的水准面相切,从比较大的区域来看,水准测量是沿着水准面进行的,两已知水准点的高差实际上是通过此两点的水准面之间的高差,但是水准面之间并不平行,故需对所测原始高差进行不平行改正。而这种改正分为两部分,一部分由于重力加速度随纬度变化引起的正常部分,另一部分是由于地壳内部质量分布不均而引起的异常部分。随纬度变化引起的正常部分即正常水准面不平行改正ε,按公式(3) 计算:
| $\varepsilon =-({{\gamma }_{i+1}}-{{\gamma }_{i}}).{{H}_{m}}/{{\gamma }_{m}}$ | (3) |
其中,γm为两水准点正常重力平均值,单位为10-5 m/s2;γi、γi+1为i点、i+1点椭球面上的正常重力值,单位为10-5 m/s2;Hm为两水准点概略高程平均值,单位为m。
| ${{\gamma }_{m}}=({{\gamma }_{i}}+{{\gamma }_{i+1}})/2-0.1543{{H}_{m}}$ | (4) |
| $\gamma =978032(1+0.0053024{{\sin }^{2}}\varphi -0.0000058{{\sin }^{2}}2\varphi )$ | (5) |
其中,φ为水准点纬度。
例如:设A、B点纬度分别为34.005°、34.006°,代入公式(3) 、(4) 、(5) 可得ε=-0.07 mm。
1.3 重力异常改正由于地壳内部物质质量的不均匀性会引起重力加速度的变化,使得地面点实测重力加速度g与相应的正常重力加速度γ不相等,产生差值Δg,Δg=g-γ,所以必须加入重力异常改正[2] 。
用重力仪所测的原始结果g测,通过纬度、高度、地形、中间层改正后,再减去正常重力值所得之差,称做布格重力异常Δg,即
| $\Delta g=\left( {{g}_{测}}+{{g}_{纬}}+{{g}_{形}}+{{g}_{中}}-\gamma \right)=g-\gamma $ | (6) |
| $\lambda ={{(g-\gamma )}_{m}}\cdot h/{{\gamma }_{m}}$ | (7) |
其中,(g-γ)m为两水准点空间重力异常平均值,单位为10-5 m/s2;h为测段观测高差,单位为m。
(g-γ)空是水准点空间重力异常,其数值由式(8) 计算:
| ${{(g-\gamma )}_{空}}={{(g-\gamma )}_{布}}+0.1119H$ | (8) |
其中,H为水准点概略高程,单位为m;水准点的布格重力异常(g-γ)布可以从地震部门或者测绘部门的相应数据库查询得知[1]。故两水准点A、B的空间重力异常平均值(g-γ)m由式(9) 计算:
| ${{(g-\gamma )}_{m}}=[{{(g-\gamma )}_{空A}}+{{(g-\gamma )}_{空B}}]/2$ | (9) |
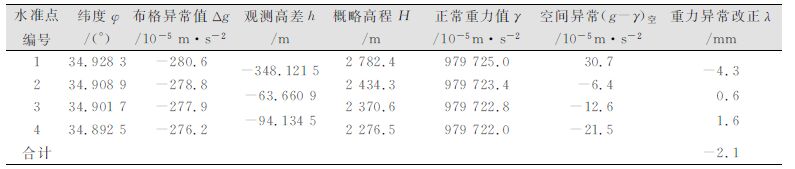
将式(9) 计算数值代入式(7) 即可求出重力异常改正λ。表 1为某条水准路线的重力异常计算数据。
| 表 1 重力异常改正数计算 Table 1 Correction Calculation of Gravity Anomaly |
 |
2 环闭合差计算实例
在中国综合地球物理场观测——大华北地区项目的地震监测精密水准网中,选取其中的两个相邻水准环,如图 1所示。水准环线路Ⅰ长约700 km,水准环线路Ⅱ长约650 km。
水准环Ⅰ由路线AB、BC、CF、FG、GA构成,水准环Ⅱ由路线CD、DE、EF、FC构成,它们有公共边CF,每条线路由若干区段组成,相应线路的基本数据见表 2、表 3,其中k为路线长度。因为每条路线并不是都由一个作业小组完成,即不是用同一副标尺,故水准标尺改正系数f不是同一值,因此在图 1计算∑h时,需考虑δ的影响,即∑h=∑(δ+h)。
 |
| 图 1 水准路线独立环示意图 Figure 1 Independent Ring Schematic Level Line |
从图 1和表 2可知,水准环Ⅰ的闭合差为:W=-29.89+1.56-4.40=-32.73 mm,其绝对值|-32.73|<
表 3中,计算线路CF、GA、DE时,对应的∑h、∑ε、∑λ的数值需反号,因为其为其他环的公共边,在每个独立环中,计算方向不同:顺时针为原号,逆时针为反号。
| 表 2 水准环Ⅰ计算 Table 2 Calculation of Level Ring Ⅰ |
 |
| 表 3 水准环Ⅱ计算 Table 3 Calculation of Level Ring Ⅱ |
 |
从图 1和表 3可知,水准环Ⅱ的闭合差为:W=+73.09-6.97-13.95=+52.17 mm >
实际测量中由于测量误差的存在,总有某些测段、区段、路线不符值超出限差,在分析原因后,必须进行重测[3],只有当这几项均合乎限差后,才可将这些数据作为计算环闭合差的原始资料;即使每一测段、区段、路线不符值均满足要求,经加入水准标尺长度改正计算δ、正常水准面不平行改正计算ε、重力异常改正计算λ时仍有可能使环闭合差超限,对于超限的数据,应对造成环闭合差超限的原因进行深入分析,如仪器因素、观测环境因素、气候气象因素、人为因素等等[4],也可以对比已有的历史成果,弄清楚究竟是哪方面的原因,然后有针对性的对某些区段的测段进行连续重测,最终使环闭合差满足允许的限差要求,为地震预报部门拿出一份精确、可靠的数据,服务于地震事业。
| [1] | GB/T 12897-2006.国家一、二等水准测量规范[S].中国国家标准化管理委员会, 2006 GB/T 12897-2006.Specifications for the First and Second Order Leveling [S]. Standardization Administration of the People’s Republic of China, 2006 |
| [2] |
张凤举, 张华海, 赵长胜, 等.
控制测量学[M]. 北京: 煤炭工业出版社, 1999 .
Zhang Fengju, Zhang Huahai, Zhao Changsheng, et al. Control Surveying[M]. Beijing: Coal Industry Press, 1999 . |
| [3] |
潘正风, 杨正尧.
数字测图原理与方法[M]. 武汉: 武汉大学出版社, 2002 .
Pan Zhengfeng, Yang Zhengyao. Digital Mapping Principle and Method[M]. Wuhan: Wuhan University Press, 2002 . |
| [4] |
孔祥元, 郭际明, 刘宗泉.
大地测量学基础[M]. 武汉: 武汉大学出版社, 2001 .
Kong Xiangyuan, Guo Jiming, Liu Zongquan. Foundation of Geodesy[M]. Wuhan: Wuhan University Press, 2001 . |
 2016, Vol. 41
2016, Vol. 41

