| 基于小波变换的组合模型在桥梁变形分析中的应用 |
2. 兰州交通大学测绘与地理信息学院,甘肃 兰州,730070;
3. 陕西铁路工程职业技术学院测绘与检测学院,陕西 渭南,714000
2. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China;
3. School of Surveying & Testing, Shaanxi Railway Institute, Weinan 714000, China
近几十年来,高速铁路建设中以桥代路的比率越来越高,由于复杂地质条件的影响,桥梁在铁路运营过程中会产生相应的变形。因此,桥梁变形监测工作为高速铁路施工提供了有力保障。影响桥梁变形监测的主要因素有仪器精度、监测环境和人为因素,所以监测数据包含了真实信号和噪声信号。其中,噪声信号会对实际变形信息产生一定的影响,对噪声信号进行一定的消除和减弱,可以提高变形数据的精度,为后期的预测预报提供高质量的基础信息[1-4]。
本文针对桥梁变形监测数据噪声的特点,比较了小波去噪、卡尔曼滤波去噪以及小波-卡尔曼滤波、卡尔曼滤波-小波组合模型的去噪效果,并根据去噪后的数据建立了GM(1,1)模型,结合相关高速铁路桥梁变形数据,分析模型的去噪效果和预测效果。
1 小波分析小波变换是用小波函数系表示或逼近一个信号或者函数。小波函数系由一个基本小波函数经过伸缩和平移得到。
设一个基本小波Ψ (t)∈ L2 (R),其中,t表示时间,L2 (R)表示平方可积的函数空间。其傅里叶变换
| $ C_{w}=\int_{-\infty}^{+\infty}|\hat{\varPsi}(w)|^{2} w^{-1} \mathrm{~d} w<\infty $ | (1) |
{Ψa,b(t)}是Ψ(t) 进行平移和伸缩的小波函数集,表示如下:
| $ \varPsi_{a, b}(t)=|a|^{-\frac{1}{2}} \varPsi\left(\frac{t-a}{b}\right) $ | (2) |
式中,a、b分别表示平移和伸缩因子。
任意函数f(t)∈ L2 (R)的连续小波变换为:
| $ \begin{aligned} &W_{f}(a, b)=\int_{-\infty}^{+\infty} f(t) \varPsi_{a, b}(t) \mathrm{d} t= \\ &\frac{1}{\sqrt{a}} \int_{-\infty}^{+\infty} f(t) \varPsi\left(\frac{t-a}{b}\right) \mathrm{d} t \end{aligned} $ | (3) |
式(3)为连续小波函数。在实际工程应用中,变形监测所得数据都是有限长的离散信号。为了使数值计算简便,将连续小波函数进行离散化。连续小波函数离散化针对的是平移参数和伸缩参数,而不是时间变量[6, 7]。
令a=a0j,b=hb0a0j,其中,a > 1;b0 ∈ R;j、h∈ Z。将其代入式(2),便可得到离散小波函数:
| $ \varPsi_{j, h}(t)=a_{0}^{-\frac{j}{2}} \varPsi\left(\frac{t-h b_{0} a_{0}^{j}}{a_{0}^{j}}\right)=a_{0}^{-\frac{j}{2}} \varPsi\left(a_{0}^{-j}-h b_{0}\right) $ | (4) |
卡尔曼滤波是一种通过估计观测值来进行滤波的算法。由于卡尔曼滤波能够剔除随机干扰噪声,获得逼近真实信号的有用信息,因此经常被用于多噪声干扰的数据去噪[6]。卡尔曼滤波由基本方程、观测方程构成,离散化形式如下:
| $\left\{\begin{array}{l} \boldsymbol{X}_{k}=\boldsymbol{F}_{k / k-1} \boldsymbol{X}_{k-1}+\boldsymbol{G}_{k-1} \boldsymbol{W}_{k-1} \\ \boldsymbol{L}_{k}=\boldsymbol{H}_{k} \boldsymbol{X}_{k}+\boldsymbol{V}_{k} \end{array}\right. $ | (5) |
式中,Xk是系统k时刻的状态向量(n×1维);Fk/k-1是系统k-1时刻到k时刻的状态转移矩阵(n×n维);Gk-1是系统k-1时刻的动态噪声矩阵(n×r维);Wk-1是系统k-1时刻的动态噪声(r×1维);Lk是系统k时刻的观测向量(m×1维);Vk是系统k时刻的观测噪声(m×1维);Hk是系统k时刻的观测矩阵(m×n维)。
根据最小二乘原理推导卡尔曼滤波递推公式:
① 状态向量一步预测值为:
| $\hat{\boldsymbol{X}}_{k / k-1}=\boldsymbol{F}_{k / k-1} \hat{\boldsymbol{X}}_{k-1} $ | (6) |
② 状态向量一步预测值方差阵为:
| $\boldsymbol{P}_{k / k-1}=\boldsymbol{F}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{F}_{k / k-1}^{\mathrm{T}}+\boldsymbol{G}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{G}_{k-1}^{\mathrm{T}} $ | (7) |
式中,Qk-1表示k-1时刻动态噪声的方差阵。
③ 状态向量估计值为:
| $ \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{J}_{k}\left(\boldsymbol{L}_{k}-H_{k} \hat{\boldsymbol{X}}_{k / k-1}\right) $ | (8) |
式中,Jk表示滤波增益矩阵,可表示为Jk= Pk/k-1HkΤ (HkPk/k-1 HkΤ + Rk)-1,其中,Rk为观测噪声的方差阵。
④ 状态向量估计值方差阵为:
| $ \boldsymbol{P}_{k}=\left(1-\boldsymbol{J}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1} $ | (9) |
根据滤波初值
设非负离散数列为:
| $x^{(0)}=\left\{x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n)\right\} $ | (10) |
式中,n为序列长度。对x(0)进行一次累加生成,即可得到一个生成序列x(1)={x(1) (1),x(1) (2),…,x(1) (n)},对此生成序列建立如下一阶微分方程,并将其记为GM(1,1):
| $ \frac{\mathrm{d} x^{(1)}}{\mathrm{d} t}+v x^{(1)}=u $ | (11) |
式中,v和u是灰参数,其白化值为$\hat{\boldsymbol{a}}=\left[\begin{array}{ll} v & u \end{array}\right]^{\mathrm{T}}$。用最小二乘法求解,可得:
| $ \hat{\boldsymbol{a}}=\left[\begin{array}{ll} v & u \end{array}\right]^{\mathrm{T}}=\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{y}_{N} $ | (12) |
式中,$\boldsymbol{B}=\left[\begin{array}{cc} -\frac{1}{2}\left(x^{(1)}(2)+x^{(1)}(1)\right) & 1 \\ -\frac{1}{2}\left(x^{(1)}(3)+x^{(1)}(2)\right) & 1 \\ \vdots & \vdots \\ -\frac{1}{2}\left(x^{(1)}(n)+x^{(1)}(n-1)\right) & 1 \end{array}\right]$; $\boldsymbol{y}_{N}=\left[\begin{array}{c} x^{(0)}(2) \\ x^{(0)}(3) \\ \vdots \\ x^{(0)}(n) \end{array}\right]$。
求出$\hat{\boldsymbol{a}}$后代入式(11),解出微分方程:
| $ \hat{x}^{(1)}(k+1)=\left(x^{(0)}(1)-\frac{u}{v}\right) \mathrm{e}^{-v k}+\frac{u}{v} $ | (13) |
对$\hat{x}^{(1)}(k+1)$作累减生成,可得还原数据:
| $\begin{aligned} \hat{x}^{(0)}(k+1)=\hat{x}^{(1)}(k+1)-\hat{x}^{(1)}(k) \\ \text { 或 } \quad \hat{x}^{(0)}(k+1)=\left(1-\mathrm{e}^{v}\right)\left(x^{(1)}(1)-\frac{u}{v}\right) \mathrm{e}^{-v k} \end{aligned} $ | (14) |
式(13)、式(14)即为灰色预测的两个基本模型。当k < n时,称$\hat{x}^{(0)}(k)$为模型虚拟值;当k=n时,称$\hat{x}^{(0)}(k)$为模型滤波值;当k > n时,称$\hat{x}^{(0)}(k)$为模型预测值[9-12]。
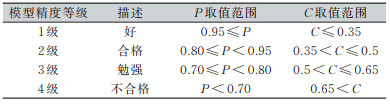
3.2 GM(1,1)模型的精度评定模型精度的评价方法有3种,分别是残差大小检验、关联度检验、后验差检验。常用后验差检验对GM(1,1)模型进行精度评价,后验差检验是对残差分布的统计检验,通常由后验差比值C和小误差概率P评价[12-16]。表 1列出了根据C、P取值确定的模型精度等级。模型精度等级判别式为:模型精度等级=max{P所在的级别,C所在的级别}。
| 表 1 GM(1,1)模型精度等级 Tab.1 Accuracy Grades of GM(1, 1)Model |
 |
4 实例分析 4.1 工程简介
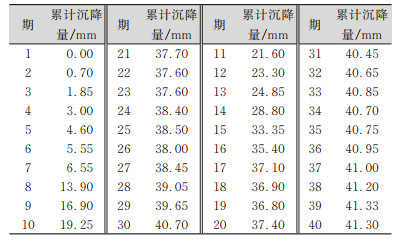
表 2为2009—2010年某高速铁路大桥桥墩的变形监测数据,共40期(数据选用的是文献[3]中所测数据)。本文以此数据为原始数据,利用MATLAB进行小波去噪、卡尔曼滤波去噪以及小波-卡尔曼滤波组合去噪,并运用GM(1,1)模型对变形进行预测。
| 表 2 沉降观测数据 Tab.2 Settlement Observation Data |
 |
4.2 数据去噪
本文用小波去噪、卡尔曼滤波、小波-卡尔曼滤波和卡尔曼滤波-小波模型对26~35期数据进行去噪处理。小波采用db10进行3层分解。去噪前后的数据如图 1所示。
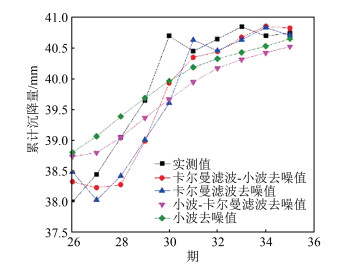 |
| 图 1 去噪前后数据对比 Fig.1 Comparison of Data Before and After Denoising |
由图 1可知,经小波去噪、小波-卡尔曼滤波组合去噪的数据较卡尔曼滤波去噪和卡尔曼滤波-小波去噪更加光滑、波动变化小,且保留了有用信号的完整性,很好保持了桥梁变形的本质特征和变化规律,其去噪效果较另外两种模型去噪效果更好。
4.3 模型预测及精度评定在去噪数据基础上,选取26~35期数据进行拟合,对36~40期数据进行预测。选用原始实测数据、经小波去噪的数据、经卡尔曼滤波去噪的数据、经小波-卡尔曼滤波去噪的数据和经卡尔曼滤波-小波去噪的数据进行预测,得到图 2所示结果,并与实测值进行对比,得到表 3所示结果。
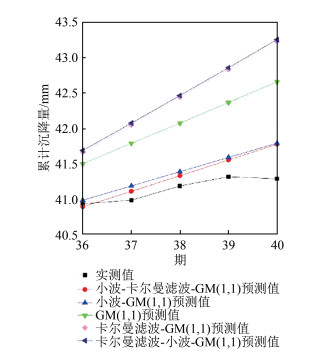 |
| 图 2 模型预测结果 Fig.2 Prediction Results of Models |
| 表 3 预测值与实测值对比 Tab.3 Comparison of Predicted and Measured Values |
 |
由图 2可知,与其他模型相比,小波-GM(1,1)模型和小波-卡尔曼滤波-GM(1,1)模型的预测值更加接近实测值。由表 3也可以看出,小波-卡尔曼滤波-GM(1,1)模型预测值的最大残差为-0.48 mm,最小残差为0.04 mm,小于其他模型的残差。
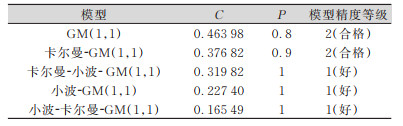
由表 4可知,小波-卡尔曼滤波-GM(1,1)模型的后验差比值为0.165 49,小误差概率为1,其模型精度相比其他模型有明显提高。这说明先进行小波去噪后进行卡尔曼滤波去噪,可以有效减弱随机误差噪声对于预测结果的影响。
| 表 4 模型精度对比 Tab.4 Precision Comparison of Models |
 |
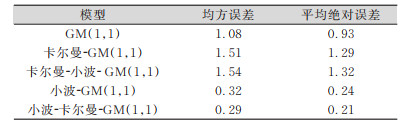
由表 5可知,小波-卡尔曼滤波-GM(1,1)模型的预测误差是5种模型中最小的。先进行小波去噪能在一定程度上消除噪声干扰,再进行卡尔曼滤波可以优化去噪效果,使数据更加接近真实的变形值。
| 表 5 模型预测误差/mm Tab.5 Prediction Error Values of Models/mm |
 |
5 结束语
本文介绍了小波去噪、卡尔曼滤波和GM(1,1)模型的基本原理。基于3种理论基础,建立去噪模型对数据进行去噪处理,并用GM(1,1)模型对去噪后的数据进行预测。对比分析4种模型的预测精度,可以发现小波-卡尔曼滤波-GM(1,1)模型的预测精度最高,小波-GM(1,1)模型的预测精度次之。分析可知,由于高速铁路桥梁变形监测过程中影响因素众多,小波去噪可以一定程度上消除噪声误差的干扰,最大程度保留真实信号数据。但是,由于白噪声的频率覆盖整个频率轴,小波去噪难以消除白噪声的影响,而卡尔曼滤波可以较好地消除白噪声的影响,提高数据的有效性,为后续工作提供可靠的信息。由此可见,基于小波-卡尔曼滤波的GM(1,1)模型在含有复杂噪声干扰的桥梁变形分析预测预报中有较强的适应性。
| [1] |
黄声享, 尹晖, 蒋征. 变形监测数据处理: 第2版[M]. 武汉: 武汉大学出版社, 2010.
|
| [2] |
谭超. 基于小波去噪-灰色预测混合模型在变形监测中的应用研究[D]. 西安: 西北大学, 2016
|
| [3] |
王建波, 栾元重, 许君一, 等. 小波分析桥梁变形监测数据处理[J]. 测绘科学, 2012, 37(3): 79-81. |
| [4] |
文鸿雁. 基于小波理论的变形分析模型研究[D]. 武汉: 武汉大学, 2004
|
| [5] |
吴杰, 余腾, 郭冰, 等. 小波神经网络在桥梁变形预测中的应用[J]. 测绘科学, 2017, 42(11): 74-79. |
| [6] |
栾元重, 栾亨宣, 李伟, 等. 桥梁变形监测数据小波去噪与Kalman滤波研究[J]. 大地测量与地球动力学, 2015, 35(6): 1 041-1 045. |
| [7] |
王建波. 小波变换在桥梁变形监测数据处理中的应用[D]. 青岛: 山东科技大学, 2011
|
| [8] |
郑健, 谢先武, 刘胜. 小波分析法高铁沉降变形预测[J]. 测绘科学, 2016, 41(4): 161-164. |
| [9] |
刘闯, 花向红, 赵杰, 等. 基于小波去噪的高铁沉降预测模型研究[J]. 测绘地理信息, 2015, 40(1): 37-40. |
| [10] |
陈晨, 魏冠军, 寇瑞雄, 等. 基于Kalman滤波的GM(1, 1)-AR模型在高层建筑物沉降变形分析中的应用[J]. 测绘工程, 2018, 27(10): 64-67. |
| [11] |
姜刚, 杨志强, 张贵钢. 卡尔曼滤波算法的灰色理论模型在变形监测中的应用[J]. 测绘科学, 2011, 36(4): 19-21. |
| [12] |
卜璞, 李朝奎, 廖孟光. 改进GM(1, 1)模型在建筑沉降变形观测中的应用[J]. 测绘通报, 2016(12): 60-63. |
| [13] |
陈亮, 黄腾. 基于灰色关联分析的卡尔曼滤波在桥梁变形监测中的应用[J]. 测绘工程, 2010, 19(4): 47-49. DOI:10.3969/j.issn.1006-7949.2010.04.013 |
| [14] |
高红, 文鸿雁, 李运健, 等. 基于小波变换与卡尔曼滤波结合的GM(1, 1)模型在高铁隧道沉降变形分析中的应用[J]. 现代隧道技术, 2016, 53(4): 84-89. |
| [15] |
刘兆惠, 李倩, 王超, 等. 基于小波卡尔曼滤波的高速公路交通数据融合去噪算法研究[J]. 公路工程, 2018, 43(6): 91-96. DOI:10.3969/j.issn.1674-0610.2018.06.018 |
| [16] |
焦明连, 蒋廷臣. 基于小波分析的灰色预测模型在大坝安全监测中的应用[J]. 大地测量与地球动力学, 2009, 29(2): 115-117. |
 2022, Vol. 47
2022, Vol. 47

