灰色模型要求原始数据等时距，但在实际应用中，若原始数据光滑程度不够，利用灰色模型预测时容易出现较大误差^[1-4]。常规方法是使用紧邻均值公式平滑灰色模型原始序列优化背景值，使用优化后的序列进行参数求解^[5-9]。实际上，紧邻均值的优化公式就是数值积分中的梯形公式，此公式的Cotes系数中n = 1 ^[10-13]。灰色模型一般仅适用于短期预测，因此需要对该模型进行优化。

数值积分中，随着数值求积的Cotes系数的递增，当n = 2时即为辛普森公式。为提高灰色模型预测精度，本文尝试使用辛普森公式代替梯形公式，以优化背景值，得到光滑度更好的原始序列。

1 梯形公式优化背景值的灰色模型

设等间隔离散非负序列：

$x^{(1)}=x^{(1)}(1), x^{(1)}(2), x^{(1)}(3), \cdots, x^{(1)}(n) \text {, 对 } x^{(1)}$进行一次累加，则有：

$ x^{(2)}(k)=\sum\limits_{i=1}^k x^{(1)}(i), k=1, 2, 3, \cdots, n $

(1)

由此得到累加序列：

$x^{(2)}=x^{(2)}(1), x^{(2)}(2), x^{(2)}(3), \cdots, x^{(2)}(n)$。

对$x^{(2)}$进行背景值优化，生成紧邻均值序列$x^{(3)}=x^{(3)}(2), x^{(3)}(3), \cdots, x^{(3)}(n)$，其中$x^{(3)}(k)=1/2\left[x^{(2)}(k)+x^{(2)}(k+1)\right], k=2, 3, \cdots, n$。

建立关于$x^{(2)}$的一阶白化微分方程：

$ \frac{\mathrm{d} x^{(2)}}{\mathrm{d} t}+a x^{(2)}=b $

(2)

用最小二乘法求待定系数a、b：

式中，$\begin{gathered} {\left[\begin{array}{ll} a & b \end{array}\right]^{\mathrm{T}}=\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{Y}} \\ \boldsymbol{B}=\left[\begin{array}{cc} -x^{(3)}(2) & 1 \\ -x^{(3)}(3) & 1 \\ \vdots & \vdots \\ -x^{(3)}(n) & 1 \end{array}\right] ; \boldsymbol{Y}=\left[\begin{array}{c} x^{(2)}(2) \\ x^{(2)}(3) \\ \vdots \\ x^{(2)}(n) \end{array}\right] \end{gathered}$。

求出待定系数后，可得具体时间响应公式：

$ \begin{gathered} x^{(2)}(k+1)=\left[x^{(1)}(1)-\frac{b}{a}\right]^{\mathrm{e}^{-a t}}+b/a, k= \\ 1, 2, 3, \cdots, n \end{gathered} $

(3)

由于求得的$x^{(2)}$ (k)序列是累加以后的，因此需要进行累减，将其还原为原始序列的预测值^[14]。

2 辛普森公式优化背景值的灰色模型

插值型数值积分求积公式为：

$ I_n=(b-a) \sum\limits_{k=0}^n C_k^{(n)} f\left(x_k\right) $

(4)

式中，C_k⁽ⁿ⁾为Cotes系数。

当n = 1时，梯形公式形式如下：

$ T=\frac{b-a}{2}[f(a)+f(b)] $

(5)

紧邻均值公式如下：

$ x^{(3)}(k)=1/2\left[x^{(2)}(k)+x^{(2)}(k+1)\right] $

(6)

两式的区别在于式（5）存在b-a，但k + 1 - k = 1，因此该项为1，由此可知两式的形式完全一致，紧邻均值公式即为梯形公式^[15]。将辛普森公式引入背景值优化，辛普森公式原始形式如下：

$ S=\frac{b-a}{6}\left[f(a)+4 f\left(\frac{a+b}{2}\right)+f(b)\right] $

(7)

将式（7）用于背景值优化，计算公式如下：

$ x^{(3)}(k)=\frac{1}{6}\left[x^{(2)}(k)+4 x^{(2)} \frac{2 k+1}{2}+x^{(2)}(k+1)\right] $

(8)

$\frac{2 k+1}{2}$不是恒为整数，因此在实际计算时，可将小数向下取整，将式（8）进行变化，得到如下公式：

$ \begin{gathered} x^{(3)}(k)=\frac{1}{6} \times\left[x^{(2)}(k)+4 x^{(2)}\left[\frac{2 k+1}{2}\right]+\right. \\ \left.x^{(2)} \times(k+1)\right] \end{gathered} $

(9)

式中，[]表示向下取整函数。

用式（9）替换式（6）进行灰色模型预测，即为辛普森公式优化背景值的灰色模型^[16]。

3 实例验证 3.1 工程概况

某商业综合体项目，拟建基坑深度约11.2 m。商业综合体为地下两层、地上23层，基础形式为筏板基础，主体车库基坑面积为11 858.58 m²，基坑长约165.3 m，宽约96.7 m，深度约11.2 m，汽车坡道基坑面积约为914.3 m²，深度为1.25~5.1 m，主体车库基坑开挖深度为10.9~11.2 m。根据周边环境，划分如下支护剖面：道路保护区范围外的3-3剖面和6-6剖面，其中6-6基坑邻近既有道路，下方管线密集，安全等级为一级；建筑物保护区范围内的4-4剖面和5-5剖面安全等级均为一级，其中5-5剖面与建筑物的水平净距为6.2~12 m，均采用桩+预应力锚索支护，肥槽宽度为0.8 m。

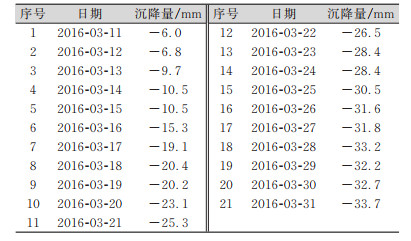
3.2 沉降模拟

取该基坑地表沉降点DB2-4进行实例验证，测量时段为2016-03-11—2016-03-31，共21期数据，原始数据如表 1所示。

使用梯形公式优化背景值的灰色模型和辛普森公式优化背景值的灰色模型预测该数据，将预测结果−真值作为预测残差，绘制残差结果图，见图 1。

由图 1可得出如下结论：①梯形公式预测残差较大，正值范围内最大可达6 mm，负值范围内可到-8 mm；预测残差呈现散乱式分布，效果较差；预测前期，梯形公式残差很大，随着时间推移，残差开始减小，但在预测中期残差一直下降，达到了一个负值范围内较大的程度；在预测中期，残差变化无明显规律，在预测后期，残差开始在正数范围内逐渐增大。②辛普森公式的预测残差相对较小，正值范围内最大在4 mm左右，负值范围内可到-4 mm；预测残差比较平稳，预测中期开始呈现灰色模型特有的指数增长趋势；预测前期，辛普森公式残差较大，但在预测中期残差开始趋于平稳，保持在-2~2 mm之间；预测后期，由于灰色模型自身存在的指数性质（可由式（3）看出，对不同期数的预测，仅有指数上的k有变化），后期预测会逐渐类似指数增长趋势而增长。

为直观评价两种模型的预测效果，采用观测值的中误差评定精度，计算公式如下：

$ m=\sqrt{\frac{[v v]}{n-1}} $

(10)

式中，v为残差值；n为数据期数。

使用梯形公式计算得到的中误差为4.001 mm，而使用辛普森公式优化背景值后，得到的中误差为2.577 mm，预测精度提高了64.39%。这表明使用辛普森公式优化背景值在短期预测中有一定的使用价值。

4 结束语

本文通过数值积分求积的推导，验证了紧邻均值公式即为梯形公式；在Cotes系数n = 2时使用了辛普森公式，根据数据实际情况用公式$x^{(3)}(k)=\frac{1}{6}\left[x^{(2)}(k)+4 x^{(2)}\left[\frac{2 k+1}{2}\right]+x^{(2)}(k+1)\right]$在灰色模型中优化背景值。结果表明：梯形公式预测残差较大，从开始的较大正残差，逐渐演变为绝对值较大的负残差，而后又持续变为正残差，预测残差值在0附近持续波动且幅度较大，这种波动无明显的规律和趋势，总体而言，残差预测范围为-8~6 mm，预测中误差为4.001 mm；辛普森公式预测残差相对较小，总体与梯形公式类似，也呈由正而负再回正的大趋势，虽然残差也在0附近持续波动，但幅度较小，残差折线更为平滑，总体而言残差预测范围为-4~4 mm，预测中误差为2.577 mm。

综上所述，辛普森公式优化背景值的灰色模型能有效提高预测精度，预测中误差仅为2.577 mm，可以用于工程测量中的短期预测。