| 基于贝叶斯概率统计的GPS载波相位周跳探测与修复方法 |
2. 地球空间信息技术协同创新中心,湖北 武汉,430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
在全球定位系统(global positioning system, GPS)高精度数据处理中,对载波相位观测值进行预处理,周跳探测与修复是一个关键问题。准确高效地探测与修复周跳,将为后续定位计算提供“干净”数据,为整周模糊度固定以及高精度定位奠定基础[1]。
GPS载波相位的原始观测值受各种误差的影响,很难对周跳进行标记与计算,因此周跳的探测与修复一般从两个方面展开:①构建各种线性组合观测值来消除某些误差的影响,使周跳脱离于各种误差影响而显现出来,常用的组合主要有Melbourne-Wubbena(MW)组合[2, 3]、Geometry-Free组合[2, 3]、电离层残差组合[4]等;②组合观测值构建之后,需要采用适当的数学模型客观地将周跳标记出来并加以修复,常用的方法有高次差法、多项式线性拟合法[5]、卡尔曼滤波法[6]、小波变换法[7]等。当载波频率数一定时,可利用的组合是有限的,各种组合也有其自身的局限性和适用范围,因此,对于GPS双频数据,目前很难再从非差线性组合方面进一步研究。只有新的载波频点L5纳入之后,才会有更多可利用的组合观测值产生[8]。对于相应的组合观测值序列,如何检验周跳是否存在,如何计算周跳的大小,却可以尝试不同的数学模型与方法。
Sansò等最早提出了基于贝叶斯概率推断的GPS相位数据的整数变量估计方法[9]。其后,Lacy等提出了一种更为普遍的基于贝叶斯概率统计的多项式回归模型[10],并将其应用于GPS数据的相位周跳探测。本文研究Lacy等提出的基于贝叶斯概率统计的周跳探测与修复方法。采用该方法对一般的模拟观测值序列以及添加了确定周跳组合的原始“干净”的GPS双频数据进行处理,以验证方法的探测与修复能力。
1 数学模型 1.1 一个周跳的探测与修复对于任何原始或者组合观测值的时间序列,可以定义为y0(t1), y0(t2), …, y0(tn)。假定序列中τ时刻存在一个大小为k的周跳,则整个观测值序列可以用多项式拟合表示为:
| $\begin{array}{l} {y_0}\left( {{t_i}} \right) = \sum\limits_{j = 1}^m {{\varphi _j}\left( {{t_i}} \right){x_j}} + k{h_\tau }\left( {{t_i}} \right) + v\left( {{t_i}} \right), \\ i = 1, 2, ..., n \end{array}$ | (1) |
式中,ti为第i个历元;φj(ti)为多项式的基函数;xj为多项式的未知系数;v(ti)为观测噪声;hτ(ti)为海维塞尔函数,其向量形式为:
| ${\vec y_0} = \mathit{\boldsymbol{A}}\vec x + k{\vec h_\tau } + \vec v$ | (2) |
式中, A是一个n×m矩阵,Aij=φj(ti),n为序列中观测值个数;m为拟合多项式的阶数。为了防止矩阵A为奇异矩阵,式(2)一般采用正交多项式拟合,正交多项式的构造采用施密特正交方法[10]。
文献[11]表明,正态概率密度函数是描述GPS测量数据分布的合理模型,因此,对于式(2)中的观测噪声
| ${\vec y_0} \sim N\left( {\mathit{\boldsymbol{A}}\vec x + k{{\vec h}_\tau }, \sigma _0^2\mathit{\boldsymbol{I}}} \right)$ | (3) |
基于贝叶斯概率统计的基本理论[12],式(3)中分布的所有未知参数(
| $\begin{array}{l} p\left( {{{\vec y}_0}\left| {\vec x, \tau, k, \sigma _0^2} \right.} \right) = \\ \frac{1}{{{{\left( {2\pi \sigma _0^2} \right)}^{\frac{n}{2}}}}}{\rm{exp}}\left[{-\frac{1}{{2\sigma _0^2}}{{\left| {{{\vec y}_0}-\mathit{\boldsymbol{A}}\vec x-k{{\vec h}_\tau }} \right|}^2}} \right] \end{array}$ | (4) |
将未知参数(
计算(
| $\begin{array}{l} p\left( {\vec x, \tau, k, \sigma _0^2{\rm{|}}{{\vec y}_0}} \right) \propto \frac{1}{{{{\left( {\sigma _0^2} \right)}^{n/2 + 1}}}} \cdot \\ {\rm{exp}}\left[{-\frac{1}{{2\sigma _0^2}}{{\left| {{{\vec y}_0}-\mathit{\boldsymbol{A}}\vec x-k{{\vec h}_\tau }} \right|}^2}} \right] \end{array}$ | (5) |
为了探测周跳发生的历元,必须获取周跳发生的历元τ关于观测值序列
| $ \left\{ {\begin{array}{*{20}{c}} {p\left( {\tau {\rm{|}}{{\vec y}_0}} \right) \propto {a_\tau }^{\frac{{n - m - 2}}{2}}{{\left( {{a_\tau }c - b_\tau ^2} \right)}^{ - \frac{{n - m - 1}}{2}}}}\\ {\mathop \sum \limits_{i = 1}^n p\left( {\tau = {t_i}{\rm{|}}{{\vec y}_0}} \right) = 1} \end{array}} \right. $ | (6) |
式中,aτ=
| $\begin{array}{l} p\left( {k{\rm{|}}\bar \tau, {{\vec y}_0}} \right) = \\ \frac{{\mathit{\Gamma} \left( {\frac{{n - m}}{2}} \right)}}{{\mathit{\Gamma} \left( {\frac{{n - m - 1}}{2}} \right)}}\frac{{{{\left[{1 + \frac{{{t^2}}}{{n-m-1}}} \right]}^{ - \frac{{n - m}}{2}}}}}{{\sqrt {\pi \left( {n - m - 1} \right)} }} \end{array}$ | (7) |
式(7)的右侧显然就是自由度为n-m-1的t分布的概率密度函数,
如果观测值序列中不存在周跳,那么,当按照§1.1中的方法处理观测值时,理论上,应当无法根据式(6)获取使p(τ|
1) p(τ|
2) {t2, t3, …, tn}中没有某个历元对应的p(τ=ti|
根据特性1),如果观测值中存在1个周跳,则周跳发生的历元τ≠t1,因此式(6)可以改进为:
| $ \left\{ {\begin{array}{*{20}{l}} {p\left( {\tau |\mathop {{y_0}}\limits^ \to } \right)\infty {a_\tau }^{\frac{{n - m - 1}}{2}}{{\left( {{a_\tau }c - b_\tau ^2} \right)}^{ - \frac{{n - m - 1}}{2}}}}\\ {\sum\limits_{i = 1}^n {p\left( {\tau = {t_i}|\mathop {{y_0}}\limits^ \to } \right) = 1,其中\;p\left( {\tau = {t_1}|\mathop {{y_0}}\limits^ \to } \right) = 0} } \end{array}} \right. $ | (8) |
根据式(8)判断:如果存在1个周跳,则{t2, t3, …, tn}中某个历元对应的概率密度值较大,占主导地位;如果不存在周跳,则没有某个历元对应的概率密度值占主导地位。这里可以设置一个最小概率阈值Pmin,如果某个历元对应的概率密度值大于等于Pmin,则认为该历元对应的概率密度值占主导地位,即该历元处发生周跳;如果小于Pmin,则认为其不占主导地位,接下来就需要利用逆卡方检验来判断是否存在周跳。
假设观测值序列中不存在周跳,根据贝叶斯定理,同样可以计算σ02基于观测值序列
| $p\left( {\sigma _0^2\left| {{{\vec y}_0}} \right.} \right) \propto \frac{{{\rm{exp}}\left[{-\frac{c}{{2\sigma _0^2}}} \right]}}{{{{\left( {\sigma _0^2} \right)}^{\left( {n - m} \right)/2 + 1}}}} \Leftrightarrow \frac{{\sigma _0^2}}{c} \sim {\rm{inv}}\chi _{n - m}^2$ | (9) |
显然,如果观测值序列中不存在周跳,σ02/c服从自由度为n-m的逆卡方分布,令σ0=
首先,给定σ02的先验值
| $ \begin{array}{l} {H_0}:{P_1}\left( {\sigma _0^2 > \tilde \sigma _0^2} \right) \ge 1 - {\alpha _1}\\ {H_1}:{P_1}\left( {\sigma _0^2 > \tilde \sigma _0^2} \right) < 1 - {\alpha _1} \end{array} $ | (10) |
式中,α1为显著性水平,1-α1取值接近1。如果上述假设检验接受原假设,则说明观测值序列中存在周跳;否则,认为观测值数据中不存在周跳。
1.3 多个周跳的判断观测值序列中可能存在多个周跳,因此在使用§1.1与§1.2中的方法对序列进行处理前,首先需要判断观测值序列中是否存在多个周跳,需要采用逆卡方检验的方法[9]。
如果观测值序列中只存在1个周跳,根据贝叶斯公式,计算σ02基于观测值序列
理论上,采用贝叶斯方法可以对任何原始或组合观测值序列中的周跳进行探测与修复,其处理流程如图 1所示。
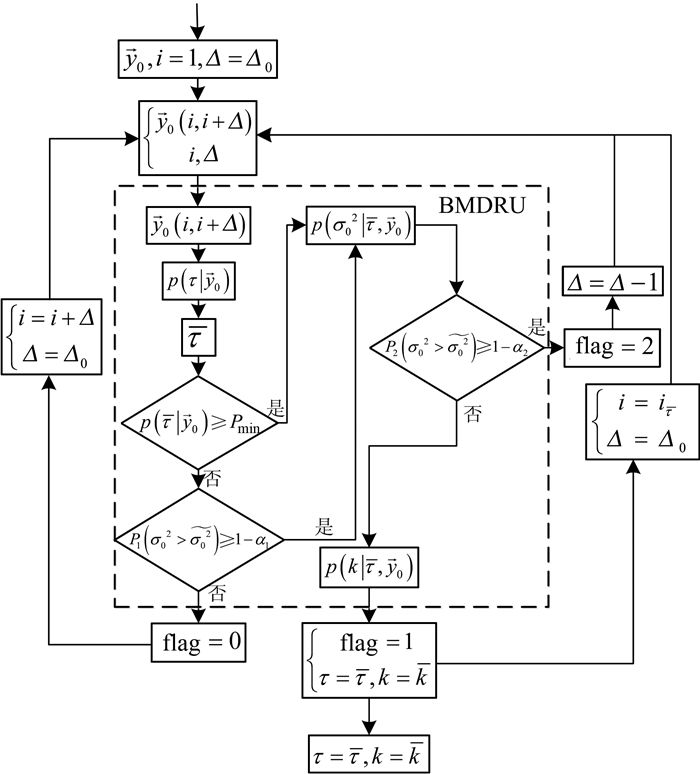 |
| 图 1 贝叶斯方法处理流程图 Figure 1 Processing Scheme of Bayesian Method |
一个完整的观测值序列为
1) flag=0时,说明
2) flag=1时,说明
3) flag=2时,说明
按照1)、2)与3)的方法循环处理,直至整个观测值序列处理完成为止。
采用GPS组合观测值序列按照图 1中的流程参与探测与修复,计算出组合周跳后,分别计算位于载波L1与L2上的原始周跳[10]。使用两种组合观测值:电离层残差(ionosphere residual,IR)组合与MW组合,两种组合观测值(ir, mw)对应的组合周跳为(k1, k2),则有:
| $ \left\{ {\begin{array}{*{20}{c}} {ir = {L_1} - {L_2}, {k_1} = {\lambda _1}\Delta {N_1} - {\lambda _2}\Delta {N_2}\quad \quad \quad \quad \;{\kern 1pt} {\kern 1pt} {\kern 1pt} }\\ {mw = \frac{{\alpha {L_1} - {L_2}}}{{\alpha - 1}} - \frac{{\alpha {P_1} + {P_2}}}{{\alpha + 1}}, {k_2} = {\lambda _w}\left( {\Delta {N_1} - \Delta {N_2}} \right)} \end{array}} \right. $ | (11) |
式中,α=f1/f2, f1、f2为频率;P1、P2为伪距观测值;L1、L2为相位观测值;λ1、λ2为波长;ΔN1、ΔN2为周跳;λw=λ1λ2/(λ2-λ1)是宽巷组合观测值的波长。
2.2 模拟序列处理实验为验证贝叶斯方法探测一个周跳的功能,模拟产生一个y(t)=at2+bt+c的二次型观测值序列,长度为60,观测噪声为σ02=1,并在31号历元处设置大小为k=4σ0的周跳,然后使用BMDRU进行处理。图 2给出了模拟观测值序列及其历元间一次差分与二次差分。显然,无论是一次差分还是二次差分,都难以判断第31号历元处存在周跳,这也说明传统的高次差法彻底失效。使用BMDRU对模拟观测值序列进行处理,图 3(a)是根据式(8)计算的p(τ|
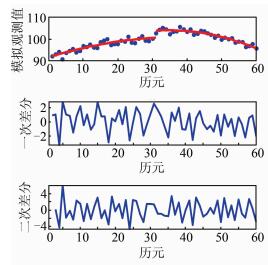 |
| 图 2 含一个周跳的模拟观测值序列及其一次差分、二次差分 Figure 2 Simulated Observation Sequence with One Cycle-slip and the First and Second Difference |
 |
| 图 3 BMDRU探测与修复概率密度分布结果 Figure 3 Probability Distribution of BMDRU for Cycle-slip Detection and Repair |
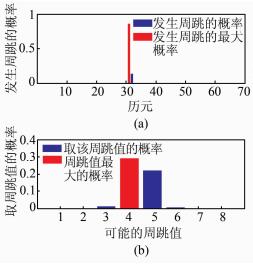
为验证贝叶斯方法探测两个周跳的功能,在观测值序列的第31个历元设置大小为k=10σ0的粗差,该粗差就相当于第31与32个历元同时发生了大小相同、符号相反的两个周跳,如图 4所示。按照图 1的流程,序列进入BMDRU模块后,结果输出flag=2,说明序列中存在多个周跳。然后逐步减小序列长度,直至只探测到1个周跳为止。按照图 1的流程自动分两段探测第1个与第2个周跳,其相应的后验概率分别如图 5所示。可以明显看出,第31与32个历元发生周跳的概率远大于其他历元,由此说明贝叶斯方法即便对相邻两个周跳都能够有效探测。
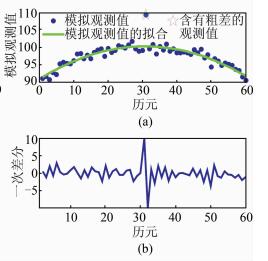 |
| 图 4 含两个周跳的模拟观测值序列及其一次差分 Figure 4 Simulated Observation Sequence with Two Cycle-slips and the First Difference |
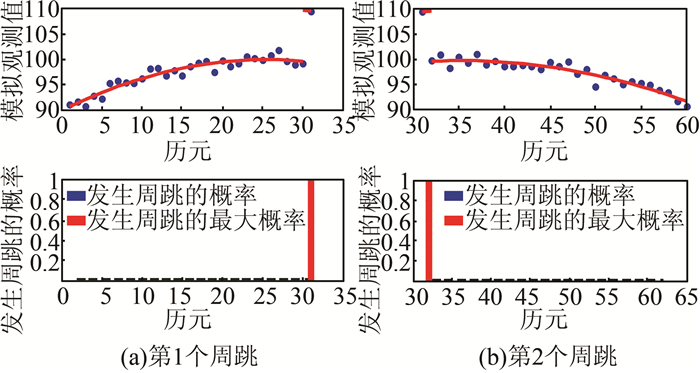 |
| 图 5 探测第1个和第2个周跳的概率分布 Figure 5 Probability Distribution of the First and Second Cycle-slips Detection |
2.3 GPS实测数据处理实验
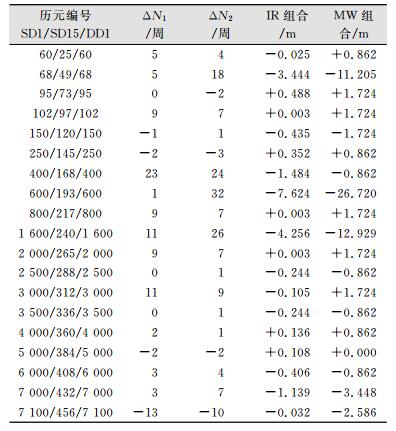
采用3种不同类型的“干净”的双频GPS实测数据进行实验:①采样间隔为1 s的静态GPS观测数据,简记为SD1(static data);②采样间隔为15 s的静态GPS观测数据,简记为SD15;③采样间隔为1 s的动态GPS观测数据,简记为DD1(dynamic data)。先对这三种“干净”数据分别加入周跳,然后用贝叶斯方法进行处理。图 6给出了3类“干净”数据的IR组合与MW组合以及历元间一次差分序列。表 1给出了载波L1与L2上设置的周跳ΔN1, ΔN2及其在IR组合和MW组合上产生的组合周跳大小。
| 表 1 设置的周跳组合 Table 1 Simulated Cycle-slips |
 |
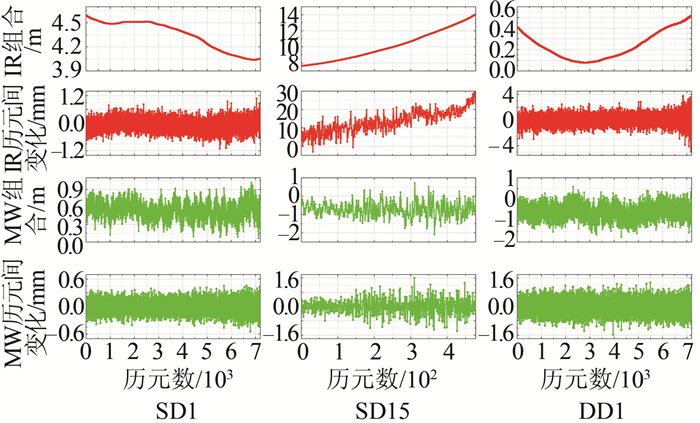 |
| 图 6 组合观测值及其一次差分 Figure 6 Combination Observations and the First Difference |
为检验贝叶斯方法的能力,载波L1与L2上设置了多个大小仅为1~2的小周跳,同时设置两种特殊的周跳组合: ①SD1/SD15/DD1第102/97/102、800/217/800与2 000/265/2 000个历元设置了大小为(9, 7)的周跳,IR组合对这种周跳组合不敏感,探测时很容易与(0, 0)或者(5, 4)混淆; ②SD1/SD15/DD1第5 000/384/5 000个历元设置了(-2, -2)的周跳,由于两种载波上的周跳相等,所以MW组合无法探测出该组合周跳。
结合图 6与表 1可以看出,对于SD1,由于测站保持静态且采样间隔较小,历元间电离层变化量小,IR组合变化量最大不超过±1 mm,而表 1中IR组合的周跳大小都在3 mm以上,因此SD1的周跳探测可以采用一次差分序列很直接地探测。对于DD1,由于测站保持动态,历元间电离层变化增大,IR组合变化量最大可达±6 mm,表 1中102/800/2 000历元的(9, 7)组合周跳极有可能被IR组合自身的变化量所掩盖而难以直接探测,因此,必须依赖MW组合探测。对于SD15数据,采样间隔增大,历元间电离层变化较大,IR组合变化量最大可达30 mm,表 1中(5, 4)、(9, 7)与(13, 10)周跳会被掩盖,因此,也必须依赖MW组合探测。
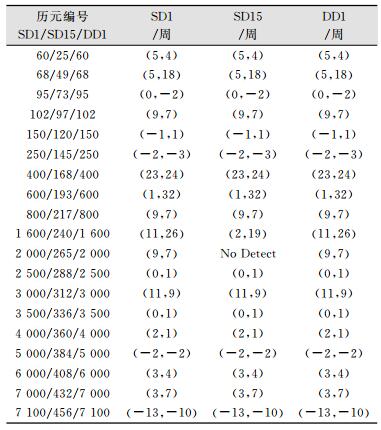
采用贝叶斯方法探测SD1、SD15与DD1的IR组合与MW组合观测值序列上的周跳结果如表 2所示,其中“No Detect”表示没有探测到。除了SD15数据的第265个历元的(9, 7)组合没有探测到,贝叶斯方法能够探测出其他所有的周跳,表现出极强的探测能力;对于已探测到的周跳,除了SD15数据的第240个历元的(11, 26)组合没有计算成功,贝叶斯方法成功修复了其他所有的周跳,表现出极强的修复能力。
| 表 2 周跳探测与修复结果 Table 2 Result of Cycle-slip Detection and Repairing |
 |
初步分析贝叶斯方法探测与修复周跳成功与失败的原因,关键在于方法本身的数学模型。贝叶斯方法是通过对整个观测值序列进行正交多项式拟合,以正态分布来描述残余的观测噪声,基于贝叶斯概率统计推断,根据验后概率来决定是否存在周跳、周跳发生的位置以及周跳的大小,其关键在于观测值序列本身是否符合正交多项式函数变化,其残余噪声是否符合正态分布。对于SD15,采样间隔较大,观测值之间的连续性减弱,观测值序列进行正交多项式拟合的前提条件减弱。此外,由于采样间隔较大,每一次进入贝叶斯方法BMDRU模块进行处理的观测值序列较短,即残余噪声序列的样本量也较小,难以体现噪声的正态分布特性,从而导致贝叶斯方法的探测与修复能力下降。当然,这种受采样间隔限制的方法也几乎是所有周跳探测方法的弱点,但这种基于概率统计推断的贝叶斯方法表现出的极强修复能力是其他方法无法比拟的。
3 结束语本文详细阐述了基于贝叶斯概率统计的周跳探测与修复方法的基本原理与数学模型,并对双频GPS观测数据进行实验处理,取得了较好的效果。贝叶斯方法具有极强的周跳探测与修复能力,但对于采样间隔较大的数据,个别历元的周跳探测与修复失败,这仍然需要进一步的研究与分析。
| [1] | 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005 |
| [2] | Blewitt G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2 000 km[J]. Journal of Geophysical Research, 1989, 94(8): 187–203 |
| [3] | Blewitt G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199–202 DOI: 10.1029/GL017i003p00199 |
| [4] | Skone S, Jong D M. The Impact of Geomagnetic Substorms on GPS Receiver Performance[J]. Earth Planets Space, 2000, 52: 1 067–1 071 DOI: 10.1186/BF03352332 |
| [5] | Westrop J, Napier M E, Ashkenazi V. Cycle Slips on the Move: Detection and Elimination[C]. The 2nd International Technical Meeting of the Satellite Division of the Institute of Navigation, Colorado, USA, 1989 |
| [6] | Blewitt G. GPS Data Processing Methodology[M]. Berlin: GPS for Geodesy, 1998 |
| [7] | Collin F, Wamant R. Application of the Wavelet Transform for GPS Cycle Slip Collection and Comparison with Kalman Filter[J]. Manuscripta Geodaetica, 1995, 20(3): 161–172 |
| [8] | 胡云龙, 唐琨, 戴鑫. GPS现代化后的周跳探测方法研究[J]. 测绘地理信息, 2016, 41(1): 14–17 |
| [9] | Sansò F, Venuti G. Integer Variables Estimation Problems: The Bayesian Approach[J]. Annals of Geophysics, 1997, 40(5): 1 415–1 431 |
| [10] | Lacy M C D, Reguzzoni M, Sansò F, et al. The Bayesian Detection of Discontinuities in a Polynomial Regression and Its Application to the Cycle-Slip Problem[J]. Journal of Geodesy, 2008, 82(9): 527–542 DOI: 10.1007/s00190-007-0203-8 |
| [11] | Tiberius C C J M, Borre K. Are GPS Data Normally Distributed[C]. International Association of Geodesy Symposia. Berlin, Heidelberg: Springer-Verlag, 2000, 121: 243-248 |
| [12] | Koch K R. Bayesian Inference with Geodetic Applications[M]. Berlin, Heidelberg: Springer-Verlag, 1990 |
 2017, Vol. 42
2017, Vol. 42

