| 精密星历对南极GPS基线解算的影响 |
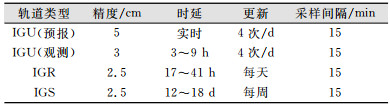
近年来,GPS技术在板块运动、卫星定轨、高空大气及冰川运动监测中发挥着越来越重要的作用[1-4]。卫星轨道精度是影响高精度GPS基线解算效果的重要因素之一[5]。GPS卫星星历的精度即GPS卫星轨道误差,是卫星星历给定的轨道与真实轨道之间的差异。对于长基线而言,轨道误差成为影响定位精度的主要因素之一。克服该误差的方法之一是采用全球GPS跟踪网所获得的精密卫星轨道,即精密星历。由于GPS解算精度与GPS卫星星历的精度密切相关,采用不同卫星星历对于相同基线的解算效果会有所不同。因此, 为了获得高精度基线解算结果,使用GAMIT进行高精度GPS基线解算时,通常采用IGS数据处理中心加权给出的事后IGS最终精密星历,但其公布的时间延迟较长,约为12~18 d,不适合时效性要求较高的基线解算。
由于南极地区特殊的地理位置和自然环境,GPS数据质量参差不齐且容易出现中断。在南极科考中,有时需要在短时间内获得高精度的基线解算结果,这时就需要使用快速星历或超快速星历,这些星历能否满足南极地区高精度基线解算的精度要求,目前还没有定论。因此,研究不同星历对基线解算的影响对于解决南极地区基线解算时效性的问题具有十分重要的意义。针对上述问题,本文利用GAMIT 10.5软件,通过选取南极地区IGS站2011年第76天单天和连续30 d的观测数据用不同星历进行解算,将03:00、09:00、15:00和21:00等4个时刻发布的IGU星历、IGR星历和IGS星历的基线解算结果进行了对比。
GPS卫星星历主要包含卫星轨道数据和卫星钟差数据。卫星星历的提供方式有广播星历和精密星历两种。由于广播星历的轨道数据精度随着时间的推移而降低,因此实际的应用有所限制[6-8]。精密星历由一些国家和组织根据各自建立的卫星参考站对导航定位卫星的跟踪观测后经处理计算出,由国际GPS服务中心发布。目前,采用国际GNSS服务组织发布的精密星历[9, 10],IGS数据处理中心为满足GPS用户对精密轨道在时间和精度上的不同需求,推出了最终星历IGS、快速星历IGR以及超快速星历IGU等3种星历产品[11-14]。GAMIT软件默认识别的星历是IGS最终精密星历,IGR、IGU与IGS格式相同,均为sp3格式文件,可以在GAMIT软件中选用。IGS最终精密星历一般滞后12~18 d发布;IGR星历滞后17~41 h发布;IGU星历含前一天24 h的观测部分和当天24 h的预报部分,每天发布4次,包括IGU00、IGU06、IGU12、IGU18,分别在03:00、09:00、15:00、和21:00等4个时刻发布。3种轨道星历产品相关参数如表 1所示。由表 1可知,时延越长,所获得的卫星轨道产品精度越高。
| 表 1 3种轨道星历产品相关参数 Table 1 Parameters of Three Satellite Ephemerides |
 |
1 GPS数据处理 1.1 数据来源
我国在南极建有长城站和中山站两个GPS常年跟踪站,为我国的南极科学考察提供了有力的基础测绘支撑与保障,也为我们进行南极地球动力学及冰川动力学研究积累了大量数据。本文选取了2011年第61~90天的长城站(GRW1)、中山站(ZHON)、南极地区的11个IGS站(CAS1、DAV1、DUM1、MAW1、MCM4、OHI2、OHI3、PALM、ROTH、SYOG、VESL)共计13个测站数据(见图 1)进行基线解算和分析。
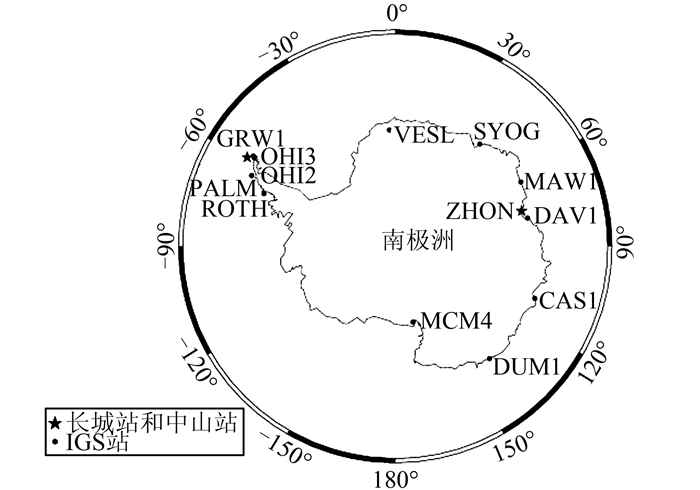 |
| 图 1 南极地区GPS站点分布图 Figure 1 Distribution of GPS Sites Used in This Study |
1.2 基线解算策略
为了对比3种星历的解算结果,本文设计了两种方案:①选取2011年第76天的数据,分别采用IGU00、IGU06、IGU12、IGU18、IGR和IGS星历先用第1 h数据解算,之后每次累加1 h数据进行解算,共计解算24次; ②选取2011年第61天到90天共30 d的数据,采用IGS、IGR星历以及方案①中解算精度最高的4个时刻的IGU星历进行解算。GAMIT 10.5基线解算策略及参考准则如下:基线解算模式设置为RELAX,同时解算测站坐标;观测值使用无电离层组合、自动修复周跳模式(LC_AUTCLN);测站先验坐标约束:IGS站为固定站,约束均为0.05 m,GRW1站和ZHON站为非固定站,约束均为100 m;截止高度角为15°;历元间隔为30 s;对流层延迟使用Saastamoinen模型;潮汐改正使用FES2004模型;参考框架为ITRF2008;其他均采用GAMIT 10.5默认设置。
2 结果与分析由于基线数目较多,本文从中选取了DAV1-ZHON和GRW1-OHI2两条基线的解算结果进行分析。图 2和图 3分别给出了基线DAV1-ZHON和GRW1-OHI2第76天采用IGS星历与IGR、IGU00、IGU06、IGU12和IGU18星历解算的3个方向基线长度的差值。从图 2、图 3中可以看出,单天采用的IGU00和IGU06星历由于实测数据很少甚至没有实测数据,基线结果与IGS星历相差较大,而采用的IGU12和IGU18星历由于实测数据开始增加,解算的结果与IGS星历相差则相对较小,在N、E方向差值不超过±1 mm,U方向差值不超过± 2 mm,采用IGR星历解算的基线与IGS星历基本一致。图 4和图 5分别给出了第61~90天共30 d DAV1-ZHON和GRW1-OHI2采用IGS星历与IGR、IGU18星历解算的基线长度差值结果,从图 4、图 5中可以看出,3个方向的基线长度差值都非常小,均在±0.7 mm以内。
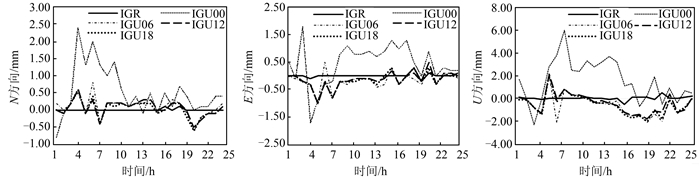 |
| 图 2 单天DAV1-ZHON基线IGS星历解算的基线长度与IGR、IGU00、IGU06、IGU12、IGU18星历解算的3个方向基线长度差值 Figure 2 Baseline Length Differences Between IGS Hourly Solutions and Other Ephemerides Hourly Solutions in DOY 76 of DAV1-ZHON Baseline |
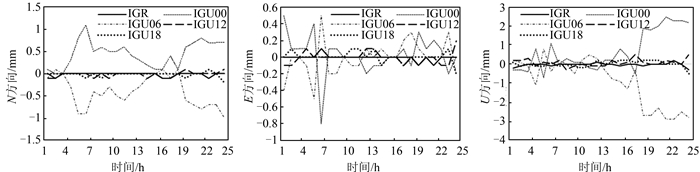 |
| 图 3 单天GRW1-OHI2基线IGS星历解算的基线长度与IGR、IGU00、IGU06、IGU12、IGU18星历解算的3个方向基线长度差值 Figure 3 Baseline Length Differences Between IGS Hourly Solutions and Other Ephemerides Hourly Solutions in DOY 76 of GRW1-OHI2 Baseline |
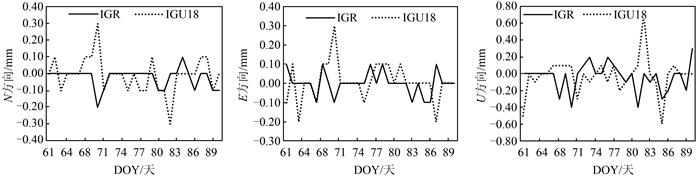 |
| 图 4 30天DAV1-ZHON基线IGS星历解算的基线长度与IGR、IGU18星历解算的3个方向基线长度差值 Figure 4 Baseline Length Differences Between IGR, IGU18 Solutions and IGS Solutions in DOY 61-90 of DAV1-ZHON Baseline |
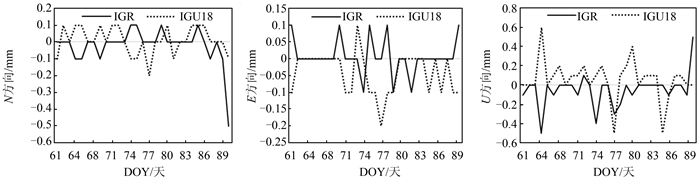 |
| 图 5 30天GRW1-OHI2基线IGS星历解算的基线长度与IGR、IGU18星历解算的3个方向基线长度差值 Figure 5 Baseline Length Differences Between IGR, IGU18 Solutions and IGS Solutions in DOY 61-90 of GRW1-OHI2 Baseline |
表 2统计了两条基线单天24组和30天使用IGS星历与使用IGR、IGU00、IGU06、IGU12、IGU18星历解算的基线长度差值的平均值。可以看出, IGR和IGS解算的基线精度相当,都略高于IGU解算的基线精度,4种IGU星历与IGR、IGS星历的差值均不超过2 mm。因此,在时效性要求较高的情况下, 可以使用IGR或IGU星历代替IGS星历在南极地区进行高精度的GPS基线解算。
| 表 2 IGS星历解算的基线长度与IGR、IGU00、IGU06、IGU12、IGU18星历解算的基线长度差值绝对值的平均值统计/mm Table 2 Mean Value of Absolute Differences Between IGS Baseline Solutions and Other Ephemeride Solutions/mm |
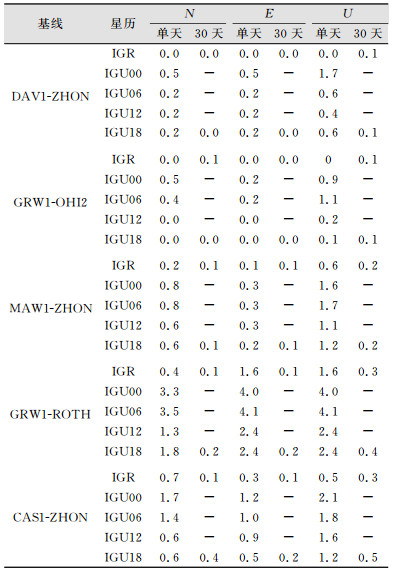 |
3 结束语
本文利用我国的长城站、中山站及南极地区的11个IGS站的数据,比较了IGS、IGR以及4种IGU星历在南极地区对GPS基线解算的影响。结果表明,单天使用IGR星历解算的基线与IGS星历精度相当,使用IGU12和IGU18星历解算的结果比IGS和IGR星历稍差,但在N、E方向差值不超过±1 mm,U方向差值不超过±2 mm,可以满足当前南极科考中GPS测量精度的要求,使用IGU00和IGU06星历基线解算结果较差;30天IGR、IGU18星历与IGS星历解算的基线长度差值3个方向均在±0.7 m以内。因此,在南极地区使用快速星历或超快速星历代替最终精密星历进行高精度基线实时解算具有可行性。
| [1] | 朱新慧, 孙付平, 秦勇. 组合GPS和VLBI数据建立板块运动模型[J]. 武汉大学学报·信息科学版, 2005, 30(7): 604–608 |
| [2] | 韩保民. 精密卫星钟差加密方法及其对星载GPS低轨卫星定轨精度影响[J]. 武汉大学学报·信息科学版, 2006, 31(12): 1 705–1 708 |
| [3] | 朱文耀, 章红平, 黄珹, 等. 利用GPS监测电离层不均匀结构探讨[J]. 地球物理学报, 2004, 47(6): 941–948 |
| [4] | 艾松涛, 王泽民, 鄂栋臣, 等. 利用GPS的北极冰川运动监测与分析[J]. 武汉大学学报·信息科学版, 2012, 37(11): 1 337–1 340 |
| [5] | 程宝银, 陈义. 应用GAMIT进行高精度GPS基线数据处理[J]. 现代测绘, 2009, 32(2): 46–48 |
| [6] | 王彬. 北斗卫星导航系统广播星历误差分析[J]. 测绘地理信息, 2015, 40(6): 25–27 |
| [7] | 楼益栋, 刘万科, 张小红. GPS卫星星历的精度分析[J]. 测绘信息与工程, 2003, 28(6): 4–6 |
| [8] | 刘伟平, 郝金明, 李作虎. 由广播星历解算卫星位置、速度及精度分析[J]. 大地测量与地球动力学, 2010, 30(2): 144–147 |
| [9] | 汪平, 许家琨, 沈国康. IGS快速精密星历与事后精密星历的定位精度分析[J]. 海洋测绘, 2015, 35(5): 32–34 |
| [10] | 李晓宇, 董绪荣, 帅玮祎. 基于超快精密星历的空间信号完好性监测算法[J]. 航天控制, 2017, 35(1): 48–53 |
| [11] | Hadas T, Bosy J. IGS RTS Precise Orbits and Clocks Verification and Quality Degradation over Time[J]. GPS Solutions, 2012, 16(4): 439–448 |
| [12] | Douša J. The Impact of Errors in Predicted GPS Orbits on Zenith Troposphere Delay Estimation[J]. GPS Solutions, 2010, 14(3): 229–239 |
| [13] | 尹继尧, 徐平, 吴培稚. 快速精密星历替代精密星历定位的初步研究[J]. 西北地震学报, 2006, 28(1): 36–41 |
| [14] | 高旺, 高成发, 潘树国, 等. 基于快速星历的GAMIT高精度基线解算研究[J]. 测绘科学, 2015, 40(2): 22–25 |
 2018, Vol. 43
2018, Vol. 43

