| 基于图像信息熵的图像分类 |
2. 武汉大学电子信息学院,湖北 武汉,430072
2. School of Electronic Information, Wuhan University, Wuhan 430072, China
信息熵这个专有名词来源于信息论[1], 它反映出某信息源X可能发出r种不同的信息a1, a2, …, ar每种信息的先验概率分别为P(a1), P(a2), …, P(ar),每种信息中均有若干相应信息组成,每种信息的特征均值为I(a1), I(a2), …, I(ar),则由r种不同的信息组成的信息源X的信息熵H(X)[1]为:
| $ \begin{array}{l} H\left( X \right) = P\left( {{a_1}} \right)I\left( {{a_1}} \right) + P\left( {{a_2}} \right)I\left( {{a_2}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\; \cdots + P\left( {{a_r}} \right)I\left( {{a_r}} \right) \end{array} $ | (1) |
式中,H(X)为信息源X的信息熵;P(ai)是信息源中第i个信息的先验概率;I(ai)是信息源中第i个信息的特征均值。
从式(1)可知,某个信息源的信息量的大小,不同的信息源可以通过相应的信息熵进行比较。我们借助信息系统中信息熵的这一特点,解决图像分类的问题。
2 图像的信息熵一幅图像的特征可以用像元的灰度表示,这就是通常的像元。再一种表示图像的特征是分形维,本文采用图像分形维特征计算图像的信息熵[2-9]。为了节省信息熵计算的时间,我们将一幅100×100像元图像划分成许多5×5的像元块,并把每个像元块称之为“大像元”,用大像元中25个像元的特征均值作为一个“大像元”的特征值。本文使用的图像信息熵是在大像元的基础上进行计算的。
假定一幅图像中每个大像元的特征为f(i, j),由该幅图像中大像元的特征,求得特征均值为fcp, 这样可以求得每个大像元的残差v(i, j)。
| $ v\left( {i, j} \right) = \left| {f\left( {i, j} \right) - {f_{cp}}} \right| $ | (2) |
和该幅图像特征的标准差m:
| $ m = \sqrt {\frac{{v\left( {i, j} \right) \times v\left( {i, j} \right)}}{n}} $ | (3) |
式中,n表示该幅图像中大像元的个数。
在这个基础上,将一幅大像元图像分为两组:第一组是大像元特征值f(i, j)与该图像大像元特征的均值fcp之差的绝对值小于或等于2m的n1个大像元组成,即有:
| $ \left| {\left( {f\left( {i, j} \right) - {f_{cp}}} \right)} \right| \le 2m $ | (4) |
在第一组中满足公式(4)的n1个大像元的特征均值为I(a1),第一组大像元的先验概率P(a1)为:
| $ P\left( {{a_1}} \right) = {n_1}/n $ | (5) |
第二组大像元数量为n2=n-n1, 第二组大像元的先验概率P(a2)为:
| $ P\left( {{a_2}} \right) = {n_2}/n $ | (6) |
在第二组中n2个大像元的特征均值为I(a2)。由式(2)~式(6),并对照式(1),可以得到适用的图像信息熵公式:
| $ H = P\left( {{a_1}} \right)I\left( {{a_1}} \right) + P\left( {{a_2}} \right)I\left( {{a_2}} \right) $ | (7) |
式中,H表示一幅图像的信息熵;P(a1)表示满足式(4)和式(5)的第一组大像元的先验概率;P(a2)表示满足式(6)大像元先验概率;I(a1)和I(a2)分别表示一、二两组大像元的特征均值。
3 采用图像信息熵的图像分类假定有A、B、C等3组不同类别的图像,每组图像分别有na、nb、nc幅图像,按式(7)分别求得每组图像的信息熵:
| $ \left\{ \begin{array}{l} {H_a}\left( i \right) = P{\left( {{a_1}} \right)_i}I{\left( {{a_1}} \right)_i} + P{\left( {{a_2}} \right)_i}I{\left( {{a_2}} \right)_i}\\ {H_b}\left( j \right) = P{\left( {{b_1}} \right)_j}I{\left( {{b_1}} \right)_j} + P{\left( {{b_2}} \right)_j}I{\left( {{b_2}} \right)_j}\\ {H_c}\left( k \right) = P{\left( {{c_1}} \right)_k}I{\left( {{c_1}} \right)_k} + P{\left( {{c_2}} \right)_k}I{\left( {{c_2}} \right)_k} \end{array} \right. $ | (8) |
式中,Ha(i)、Hb(j)、Hc(k)分别表示A、B、C等3组图像中第i、j、k幅图像的信息熵,这些信息熵都是按每幅图像的大像元求得的。
在每组图像中选择部分图像(一般选择该组图像的1/4)作为取样,计算各组图像取样的信息熵的均值,作为各组图像取样的信息熵HCPa、HCPb和HCPc。今有一幅待检验图像的信息熵Hl,分别计算Hl与3个取样信息熵之差的绝对值Δi:
| $ \left\{ \begin{array}{l} {\Delta _1} = Abc\left( {{H_l} - {\rm{HC}}{{\rm{P}}_a}} \right)\\ {\Delta _2} = Abc\left( {{H_l} - {\rm{HC}}{{\rm{P}}_b}} \right)\\ {\Delta _3} = Abc\left( {{H_l} - {\rm{HC}}{{\rm{P}}_c}} \right) \end{array} \right. $ | (9) |
式中,Δi的最小者所属类别便是待检验图像的类别。
4 实验与分析 4.1 实验中使用5种不同类别的图像实验中使用的图像分别是灌木(52幅)、居民地(23幅)、河流(35幅)、山地(20幅)、水田(13幅)等。每类图像中选择约1/4图像作为每类图像的取样,5种不同类别图像的取样分别为:灌木(14幅),居民地(5幅),河流(9幅),山地(5幅),水田(4幅)。从5种不同类别图像中选取3种不同类别图像组成一个基于信息熵图像分类的试验组。每个试验组应完成以下工作:
1) 将每幅100×100像元的图像转换为18×18大像元图像,每个大像元是由5×5像元组成的。
2) 根据式(2)~式(6)计算每幅图像的信息熵H(i)=P(a1)iI(a1)i+P(a2)iI(a2)i。
3) 选择3个不同类别的图像,如灌木、河流、居民地的组合进行分类试验。
4) 对组合图像中各类图像,按1/4的原则选出各类图像的取样,并计算各类别取样信息熵的均值:HCPa、HCPb、HCPc。
5) 在灌木、河流、居民地组合中任一幅待检验图像的信息熵为Hl,要确定该幅图像的类别,需要按式(9)计算出Hl与3个取样信息熵均值之差Δ1、Δ2、Δ3, 其中Δi的最小者所属的类别,便是待检验图像的类别。
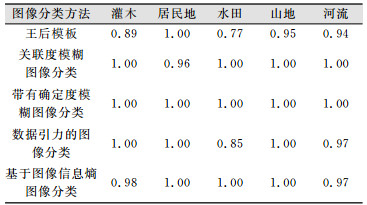
4.2 实验结果利用本文信息熵方法图像分类的结果为正确的分类数/像幅总数(分子表示该类别被正确识别的像幅数;分母表示该类别像幅的总数)。具体为灌木:51/52=0.98;居民地:23/23=1;水田:13/13=1;山地:20/20=1;河流:34/35=0.97。
本文方法与其他方法对比的图像识别情况如表 1。从表 1的对比结果可以看出,基于图像信息熵的图像分类是一个较好的分类方法。
| 表 1 本文信息熵分类结果与其他图像分类方法的对比 Table 1 Comparative Results of our Information Entropy Method with other image Classification Methods |
 |
5 结束语
表 1中实验结果是多次实验分析研究的结果。以下几个问题值得进一步分析研究:①怎样选择3个不同类别作为一个组合; ②一个组合确定了,如何合理地选择每类图像的取样。根据我们在实验中的体会,同一个类别的图像在不同的组合中,采用的取样图像可以不完全相同,但是取样的数量保持不变。通过实验中问题的解决,认为本文图像信息熵的图像分类方法是很有潜力的图像分类方法。
| [1] |
史文中. 空间数据与空间分析不确定性原理[M]. 北京: 科学出版社, 2015.
|
| [2] |
姜丹. 信息论与编码[M]. 合肥: 中国科技大学出版社, 2001.
|
| [3] |
范爱民, 郭达志. 误差熵不确定带模型[J]. 测绘学报, 2001, 30(1): 48-53. DOI:10.3321/j.issn:1001-1595.2001.01.010 |
| [4] |
郑肇葆, 郑宏. 利用数据引力进行图像分类[J]. 武汉大学学报·信息科学版, 2017, 42(11): 1 664-1 607. |
| [5] |
李欣, 李茜. 一种基于自学习的单像超分辨率方法[J]. 测绘地理信息, 2017, 42(6): 56-59. |
| [6] |
郑肇葆, 郑宏. 利用数据引力进行图像分类[J]. 武汉大学学报·信息科学版, 2006, 41(4): 482-486. |
| [7] |
许贤泽, 陈少阳, 刘盼盼, 等. 基于图像测量的花键套端面尺寸检测[J]. 测绘地理信息, 2015, 40(1): 51-54. |
| [8] |
郑肇葆, 潘励, 郑宏. 应用图像关联度的图像模糊分类[J]. 武汉大学学报·信息科学版, 2015, 40(5): 574-577. |
| [9] |
郑肇葆. 产生最佳"Tuned"模板的蜜蜂交配算法[J]. 武汉大学学报·信息科学版, 2009, 34(4): 387-390. |
 2018, Vol. 43
2018, Vol. 43

