| 乘车软件应用前后出租车寻客路径偏好分析 |
2. 武汉大学地球空间信息技术协同创新中心,湖北 武汉,430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan University, Wuhan 430079, China
出租车是城市交通系统的重要组成部分,空载状态下的出租车占据城市道路资源,加剧城市的道路拥挤以及机动车污染排放。研究出租车在寻客过程中的行为,有助于掌握出租车的运营规律、模拟出租车的运营过程,从而帮助城市交通管理部门以及出租车运营部门做出科学的运营决策。
出租车的寻客行为是指出租车处于空载状态,在道路上等待或者巡游以寻找乘客的行为。相关的研究包括出租车的寻客行为规律[1, 2]、出租车寻客行为的影响因子[3-5]以及出租车寻客行为模拟[6]。司杨等[4]基于计划行为理论确定各种因素对司机寻客决策的影响大小,认为司机对目的地的交通状况、寻客时间等的看法对选择目的地的影响最大。Sirisoma等[5]对司机展开调查,采用多项Logit模型拟合司机的寻客决策,证明了模型在拟合司机的寻客行为上具有较好的效果。这些研究大多数是在区域尺度研究司机的寻客过程,并且路径选择的相关研究在考虑路径选择的影响因素时,大多只考虑了路径的行程长度、行程时间等因素,没有考虑路径上的乘客数量、空车数量等因素的影响。
乘车软件出现之后,出租车能够接收到周围乘客的需求信息,提高了出租车的供需信息匹配,能够帮助司机更快地找到乘客。已有研究主要有乘车软件出现后出租车的营运特征统计[7, 8]、网约车的定价和准入规则等营运政策的制定[9],缺乏对司机寻客路径变化的研究。
本文选取乘车软件推广使用前后两个时间段深圳市出租车的全球定位系统(global position system, GPS)轨迹数据,提取司机在寻客过程中的历史路径集合,选取影响司机寻客路径选择的6个因子,建立多项Logit模型拟合司机的路径选择行为,从而得出司机在路径选择过程中对各因子的偏好程度,分析乘车软件使用前后偏好的变化。
1 出租车寻客路径集提取为了对司机的寻客路径选择建模,需要提取司机在起终点(origin and destination, OD)对间寻客的代表路径,构成模型的路径选择集合。首先,将研究区划分为不同的区域,以区域作为路径的起点和终点,根据司机的载客状态,提取OD对间的所有空载行程轨迹;确定代表路径的方法为:对于任一个OD对间的轨迹,判断轨迹的相似性,选取相似轨迹中的其中一条作为代表路径,本文提出一种计算路径间重合度的方法,判断相似路径。
由于GPS定位精度的影响,GPS轨迹数据与路网叠加后存在偏移,首先对数据进行地图匹配,得到GPS点所在路段,匹配后轨迹数据的主要字段包括:车牌号、采集时间、GPS经纬度、匹配的路段和载客状态。进行地图匹配后,用一系列的路段编号表示轨迹。
在确定路径选择集合时,使用最多的方法是最短路径规划算法,即计算OD点对间的N条最短路径作为路径的选择集合[10]。然而这种方法的使用场景是普通司机的路径规划问题,或出租车司机载客时的路径选择问题。当出租车司机在空载状态时,所走的路径更为曲折,显然不适合用该方法确定路径选择集合。本文设计了一种基于司机的历史轨迹确定路径集合的方法。为了判断相似轨迹,本文根据式(1)、式(2)计算历史轨迹间的重合度:
| $ {\rm{OVERLAP}}{1_{ij}} = \frac{{{l_{ij}}}}{{{l_i}}} $ | (1) |
| $ {\rm{OVERLAP}}{{\rm{2}}_{ij}} = \frac{{{l_{ij}}}}{{{l_j}}} $ | (2) |
式中,lij为轨迹i和轨迹j重合路段的长度; li和lj分别表示轨迹i和轨迹j的路径长度。
式(1)、式(2)计算的是两条轨迹的重合部分在这两条路径中的占比,当路径间的重合度OVERLAP1ij和OVERLAP2ij都大于0.7时,说明轨迹有大部分重合,两条轨迹相似。
2 寻客路径选择建模 2.1 路径选择的影响因子出租车的寻客过程受到司机的个体差异[11]、学习行为、寻客经历[3]、广播信息、乘客数量、空驶出租车的数量、载客收入、寻客时间[4-5, 12]等因素的影响。本文考虑司机选择路径时对路径的通行效率、通行成本、在路上找到乘客的概率、下趟载客行程的预期收益的要求,在寻客过程中选择路径的影响因子包括行程距离(因子1)、路径的历史乘客数目(因子2)、历史载客行程距离(因子3)、空车比(因子4)、道路通畅程度(因子5)、红绿灯数目(因子6)。
1) 行程距离。路径的长度,反映司机寻客的距离成本。即路径上所有路段的长度之和Dp。
2) 路径的历史乘客数量。研究时段内,路径上所有路段的乘客数量之和,反映司机在路径上找到乘客的概率,历史乘客数量越多,概率越大。
3) 历史载客行程距离。研究时段内,路径上历史载客行程距离的均值,路径上的历史载客行程是以该路径任一路段为起点的载客行程:
| $ {\rm{CT}}{{\rm{D}}_p} = \frac{{\sum\nolimits_{i = 1}^{{N_p}} {{D_i}} }}{{{N_p}}} $ | (3) |
式中,Di表示第i趟历史载客行程的行程距离;Np表示路径p包含的历史载客行程数目;CTDp为路径p的历史载客行程距离。该指标一定程度上可表示在该路径寻客的潜在收入,行程距离超过起步距离的情况下,行程距离越长,收入越高。
4) 空车比。研究时段内,经过路径上任一路段的空驶车辆数目Nt(C, p)与总车辆数目Nt(p)的比值。路径上的空车比越高,司机寻客的竞争越激烈。
5) 道路通畅程度。在城市道路中,车辆通畅行驶的速度为40 km/h。道路通畅指数为:研究时段内,在路径上畅通行驶的GPS点记录数目Nt(sr≥sa, p)与总GPS点记录数目Nt(0:smax, p)比值的平均值。
| $ R\left( {{s_r} \ge {s_a}|p} \right) = {\rm{mean}}\left( {\frac{{{N_t}\left( {{s_r} \ge {s_a}, p} \right)}}{{{N_t}\left( {0:{s_{\max }}, p} \right)}}} \right) $ | (4) |
式中, sa和smax分别为40 km/h和120 km/h。
6) 红绿灯数量。路径上的红绿灯数量TLt(p),反映路径的复杂度。
为了消除各因子的量纲对模型系数大小带来的影响,对因子做标准归一化处理。即对任一OD对间的任一路径上的因子cpk(k=1, 2, 3, 4, 5, 6)进行标准归一化:
| $ {c'_{pk}} = \frac{{{c_{pk}}}}{{\sum\limits_{p' \in A} {{c_{p'k}}} }} $ | (5) |
式中,A为该OD对间的路径集合;c′pk为因子归一化后的值。
2.2 寻客路径选择模型本文采用多项Logit模型拟合出租车在OD对间寻客时的路径选择,得到出租车群体对路径集中各路径的选择概率。该模型中路径的效用根据出租车路径选择影响因子:
| $ \begin{array}{l} {U_p} = {\beta _1}{c_{1p}} + {\beta _2}{c_{2p}} + {\beta _3}{c_{3p}} + {\beta _4}{c_{4p}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\beta _5}{c_{5p}} + {\beta _6}{c_{6p}} \end{array} $ | (6) |
式中,Up为路径p的效用;cpk(k=1, 2, 3, 4, 5, 6)是路径p对应上述6个因子的取值。
Logit模型是根据随机效用理论推导出来的离散选择模型[13-14]。当Logit模型的效用包含多个因子时,可以推导出多项Logit模型,其模型如下:
| $ {P_p} = \frac{{\exp \left( {{U_p}} \right)}}{{\sum\limits_{q \in A} {\exp \left( {{U_q}} \right)} }} = \frac{{\exp \left( {\sum\nolimits_{k = 1}^K {{\beta _k}{c_{pk}}} } \right)}}{{\sum\limits_{q \in A} {\exp \left( {\sum\nolimits_{k = 1}^K {{\beta _k}{c_{qk}}} } \right)} }} $ | (7) |
式中,Pp为选项p的被选概率;A为选择集。有学者使用多项Logit模型拟合司机的路径选择过程,取得了较好的拟合结果[15-16]。
采用最大似然法对该模型进行参数求解,模型的最大似然函数Alh为:
| $ {A_{lh}} = \prod\limits_p^n {P_p^{{t_p}}} $ | (8) |
式中,在任一OD对间,假设可选的路径集合A包含N条路径,把司机群体经过各路径的次数看作一个事件,则该事件可以表达为{t1, t2…tp…tn};tp为司机群体经过路径p的次数。从轨迹数据中提取OD对间,司机经过路径集中各路径的频率,作为事件的观测样本值。模型拟合的事件发生概率根据式(7)进行计算。根据最大似然法则,观测样本的发生概率是似然表达式的极大值,所以模型的参数就是式(8)取得极大值时对应的一组参数。
本文考虑到在不同起点、终点区域间,出租车在选择路径时的偏好可能不一样,因而在任一起终点OD对间建立一个模型;通过对各因子做标准归一化处理,消除因子的量纲不同对因子系数的大小产生的影响,从而用因子系数的大小反映司机对因子的偏好程度。因子系数的绝对值越大,说明司机对该因子越敏感,重视程度越高。
3 出租车路径选择偏好分析本文选择深圳市出租车的GPS轨迹数据,选取乘车软件补贴政策推出前和补贴力度最大的两个时期,分别作为乘车软件推广前和推广后的时期,即:2013年12月2日至27日和2014年2月17至3月14日,两个阶段的工作日, 各20 d,时间段为上午7:30~11:30。
以深圳市的交通小区为单位定义OD对,并选择路径集中包含的行程数目大于等于30的OD对——第1阶段有2 945对,第2阶段有2 272对,建立多项Logit模型进行拟合。以轨迹数据中统计的各路径经过频率rp作为模型真值,计算模型结果中的R方统计值(式(9)),根据R方,筛选R方大于0.8的OD对进行分析——第1阶段有1 306对区域,第2阶段有1 094对区域。
| $ R = 1-\frac{{\sum\nolimits_{i = 1}^n {{{\left( {y-\widehat y} \right)}^2}} }}{{\sum\nolimits_{i = 1}^n {{{\left( {y-\widehat y} \right)}^2}} }} $ | (9) |
式中,y为真值;
偏好因子是出租车在任一OD对间寻客时,对司机影响最大的因子。本文通过对多项Logit模型的因子进行标准归一化,消除因子量纲对该模型系数大小的影响,因而因子系数的绝对值表示因子对该模型的影响大小,绝对值最大的系数对应的因子即司机的偏好因子。
3.1 各阶段偏好因子的统计分析在任一OD对间,根据建模结果中各因子系数的绝对值大小对因子排序,排位越高的因子对出租车寻客的影响越大,然后统计OD对间各因子排在前三位的次数,结果如表 1所示。从表 1中可以得出如下结论。
| 表 1 各因子排位前3时对应的OD对数量及比例 Tab.1 Amount and Proportion of OD Pairs with Factors in Corresponding Influence Order |
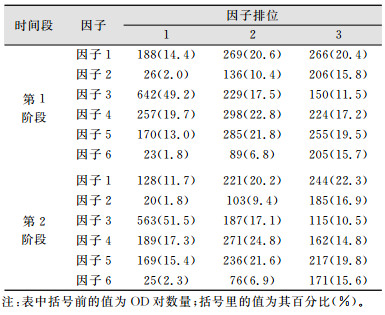 |
1) 因子3“历史载客距离”的影响最大,体现在约一半的OD对间“历史载客距离”是司机的偏好因子,且在80%左右的OD对间“历史载客距离”的影响排前三;因子1“行程距离”、因子4“空车比”、因子5“道路通畅程度”的影响大小接近,其中以“空车比”为偏好因子的OD对比另外两个因子多;因子2“历史乘客数目”和因子6“红绿灯数目”的影响最小,只有少数OD对以这两个因子为偏好因子。
2) 第2阶段与第1阶段相比,因子1“行程距离”和因子4“空车比”的影响变小,而因子5“道路通畅指数”的影响变大。“道路通畅程度”影响变大的原因可能是,第2阶段中,使用乘车软件的司机增多,乘车软件一般带有导航功能,这个功能给司机提供了实时的路况信息,能够促进这部分司机对拥堵路段的规避。
3.2 不同行政区出租车寻客偏好因子的统计分析以深圳市辖行政区为单位,统计在不同的行政区内或跨不同行政区之间,以各因子为偏好因子的OD对数目及占比。表 2展示行政区内或跨行政区行程数目超过总数目10%的结果;相较于第1阶段,第2阶段以各因子为偏好因子的OD对占比的变化如图 1所示。
| 表 2 出租车在行政区内部或跨行政区时以各因子为偏好因子的OD对数目及比例 Tab.2 Amount and Proportion of OD Pairs with Different Factors as Route Choice Preference Factors in or Across Different Administrative Regions |
 |
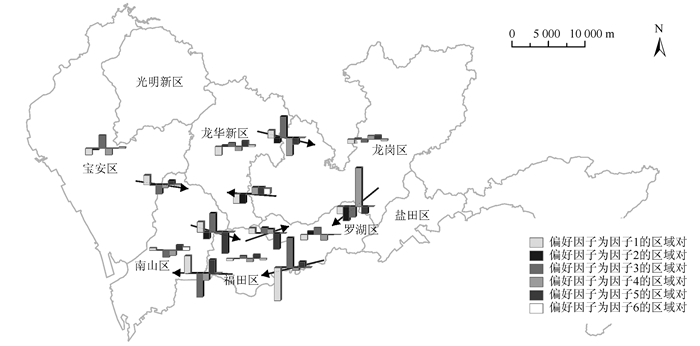 |
| 图 1 第2阶段相较第1阶段各行政区内及跨行政区间以各因子为偏好因子的OD对占比变化 Fig.1 Changes of Proportions of OD Pairs with Different Factors as Route Choice Preference Factors in or Across Different Administrative Regions in the Second Period Compared with the First Period |
从表 2可以看出:%1.5大部分司机在行政区内部寻客,且以因子3“历史载客距离”为偏好因子的OD对占比最高,即出租车在大部分的行政区内或跨行政区之间寻客时,“历史载客距离”的影响最大。但不同行政区内或不同行政区之间,以“历史载客距离”为偏好因子的OD对占比高低不一,比如:第1阶段出租车从福田到罗湖寻客时以“历史载客距离”为偏好因子的OD对占比高达77.8%,而在宝安区内的占比为35.4%。
结合表 2及图 1看出,第2阶段与第1阶段相比,出租车在行政区内寻客时,以各因子为偏好因子的OD对占比变化不大,且与深圳市整体变化相似。而跨行政区时该变化较大,且以各因子为偏好因子的OD对占比的变化与深圳整体情况不同。
4 结束语本文基于出租车的历史寻客轨迹数据,对出租车寻客路径选择偏好进行建模,并分析了乘车软件推广前后偏好的空间分布变化。实验结果表明:路径上的“历史载客行程距离”对出租车路径选择的影响最大。基于行政区分析路径选择偏好时,在大部分情况下,出租车在不同行政区内或跨不同行政区寻客时,“历史载客行程距离”的影响最大,但不同情况这个因子的影响大小有差异。相比于第1阶段,第2阶段出租车对“历史空载行程”、“道路通畅度”的敏感度增加而对“行程距离”、“空车比”的敏感度减少。本文未能考虑出租车司机的个体特征对司机路径选择偏好的影响。此外,对于乘车软件推广后的出租车寻客路径选择偏好的变化规律,仍缺乏对其产生原因的深入分析。
| [1] |
Lee W K, Sohn S Y. Taxi Vacancy Duration: A Regression Analysis[J]. Transportation Planning & Technology, 2017(4): 1-25. |
| [2] |
Liu L, Andris C, Ratti C. Uncovering Cabdrivers' Behavior Patterns from Their Digital Traces[J]. Computers Environment & Urban Systems, 2010, 34(6): 541-548. |
| [3] |
Zong Fang, Zhang Huiyong, Li Haifan. Learning Taxis' Cruising Patterns with Ripley's K Function[J]. Journal of Central South University, 2015, 22(9): 3677-3682. DOI:10.1007/s11771-015-2909-8 |
| [4] |
司杨, 关宏志. 计划行为理论下出租车驾驶员寻客行为研究[J]. 交通运输系统工程与信息, 2016, 16(6): 147-152. DOI:10.3969/j.issn.1009-6744.2016.06.023 |
| [5] |
Sirisoma R M N T, Wong S C, Lam W H K, et al. Empirical Evidence for Taxi Customer-Search Model[J]. Ice Proceedings of the Institution of Civil Engineering-Transport, 2010, 163(4): 203-210. DOI:10.1680/tran.2010.163.4.203 |
| [6] |
Li Bin, Zhang Daqing, Sun Lin, et al. Hunting or Waiting? Discovering Passenger-Finding Strategies from a Large-Scale Real-World Taxi Dataset[C].2011 IEEE International Conference on Pervasive Computing and Communications Workshops, Seattle, USA, 2011
|
| [7] |
Leng Biao, Du Heng, Wang Jianyuan, et al. Analysis of Taxi Drivers' Behaviors Within a Battle Between Two Taxi Apps[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 17(1): 296-300. |
| [8] |
Rayle L, Shaheen S, Chan N, et al. App-Based, On-Demand Ride Services: Comparing Taxi and Ridesourcing Trips and User Characteristics in San Francisco[R]. Department of Transportation's University Transportation Centers Program and California Department of Transportation, California: USA, 2014
|
| [9] |
He Fang, Shen Z J M. Modeling Taxi Services with Smartphone-Based E-hailing Applications[J]. Transportation Research Part C, 2015, 58: 93-106. DOI:10.1016/j.trc.2015.06.023 |
| [10] |
Prato C G. Route Choice Modeling: Past, Present and Future Research Directions[J]. Journal of Choice Modelling, 2009, 2(1): 65-100. |
| [11] |
Wong K I, Wong S C, Yang H, et al. Modeling Urban Taxi Services with Multiple User Classes and Vehicle Modes[J]. Transportation Research Part B Methodological, 2008, 42(10): 985-1007. DOI:10.1016/j.trb.2008.03.004 |
| [12] |
瞿嵘, 刘潇, 翁敏. 出行路径选择标准及策略研究[J]. 测绘地理信息, 2008, 33(2): 82. |
| [13] |
Domencich T A, Mcfadden D L. Urban Travel Demand: A Behavioral Analysis[M]. Amsterdam: North-Holland Publishing Company, 1975.
|
| [14] |
熊沁, 徐之俊, 李维庆, 等. 面向医疗可达性的引力模型可获性优化[J]. 测绘地理信息, 2017, 42(4): 8-12. |
| [15] |
Yao Enjian, Pan Long, Yang Yang, et al. Taxi Driver's Route Choice Behavior Analysis Based on Floating Car Data[J]. Applied Mechanics and Materials, 2013, 361-363: 2036-2039. DOI:10.4028/www.scientific.net/AMM.361-363 |
| [16] |
Dial R B. A Probabilistic Multipath Traffic Assignment Model Which Obviates Path Enumeration[J]. Transportation Research, 1971, 5(2). DOI:10.1016/0041-1647(71)90012-8 |
 2019, Vol. 44
2019, Vol. 44

