| 电离层模型IRI-2016的hmF2参数的性能评估 | [PDF全文] |
2. 武汉大学地球空间环境与大地测量教育部重点实验室,湖北 武汉,430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
国际参考电离层模型(international reference ionosphere, IRI)作为最为广泛使用的经验电离层模型,能够提供多种电离层参数的信息,如电子温度、离子温度、离子漂移等,并能计算出任意指定时间和经纬度的60~2 000 km的电子密度和总电子含量(total electron content, TEC)[1, 2]。IRI是由国际空间委员会和国际无线电联盟共同资助的项目,并在2014年成为国际标准组织(International Standards Organization, ISO)的官方电离层标准[3]。IRI建模时主要使用垂测仪、非相干散射雷达等地基观测数据以及掩星观测等卫星观测数据[4]。自1972年以来,IRI模型不断被改进并发行了多个版本,现最新版本是IRI-2016。
电离层F2层峰值高度(hmF2),即电离层电子密度最大值对应的高度,是表征电离层F2层形态的重要参量,对于许多无线电传播研究和应用有着重要的意义。传统上,由于hmF2缺少直接的观测值,峰值高度可以通过其与参数M(3000)F2的相关关系由式(1)计算得到。
| $ {\rm{hmF2}} = \frac{{1490}}{{{\rm{M}}\left( {3000} \right){\rm{F}}2 + \Delta \mathit{M}}} - 176 $ | (1) |
式中,M(3000)F2为3 000 km高度最大可用频率和F2层临界频率(foF2)的比值,hmF2单位为km; ΔM为由E层离子的延迟效应引起的改正项[5]。M(3000)F2可以直接从垂测仪记录的频高图中标定得到。在IRI-2016模型新增两种hmF2计算模型以前,使用的hmF2计算模型为CCIR模型。该模型是通过国际电信联盟无线电通信部门发布的M(3000)F2地图值计算得到hmF2。但该模型存在诸多缺陷,如模型建立时使用的数据量有限(只使用了全球分布的大约150个垂测仪在1954~1958年的数据)等。鉴于此,IRI-2016模型中新增了两种计算hmF2的模型:AMTB模型[6]和Shubin模型[7],这两种模型摆脱了对M(3000)F2值的依赖。AMTB模型是基于26个全球分布的垂测仪在1998-2006年的hmF2观测值,纯粹依靠地基垂测仪观测值进行建模。Shubin2015模型是基于CHAMP、GRACE和COSMIC掩星观测数据以及62个全球分布的垂测仪在1987~2012年的观测数据。本文使用位于磁赤道附近的垂测仪台站Jicamarca站(纬度12.0°S,经度283.2°E;地磁纬度2.1°N)在极端太阳活动低年(2008年)和太阳活动高年(2014年)的实测峰值高度hmF2来评估IRI-2016中3种hmF2模型在磁赤道地区的性能表现。
1 hmF2参数计算图 1是F10.7指数(表征太阳活动水平的指数)在2005~2016年的变化。从图中可以看出,太阳活动在2008年达到最低谷,全年的F10.7指数的平均值仅为70.6 sfu,为太阳活动的极端最小年。这次的极小年与以往相比,持续时间更长,太阳活动更低[8],对于研究IRI-2016在极端低太阳活动条件下的表现提供了可能。2014年是第24太阳活动周中太阳活动最为活跃的一年,全年的F10.7指数的平均值高达145.9 sfu(10-22·W·m-2·Hz-1)。因此,本文选用了2008年和2014年的垂测仪数据来比较IRI-2016中的hmF2模型在不同太阳活动强度下性能上的差异。
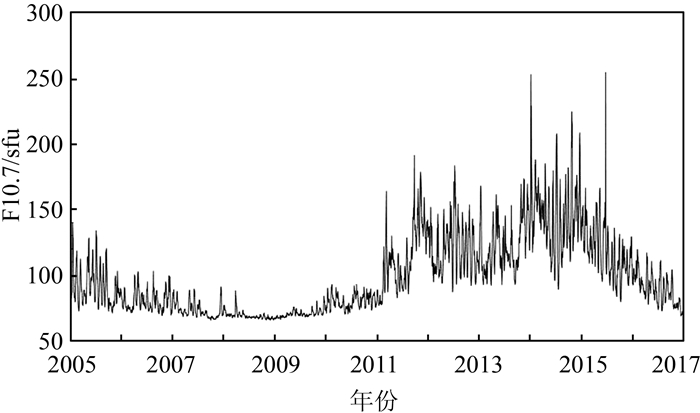 |
| 图 1 太阳活动强度变化的时间序列 Fig.1 Time Series of Solar Activity Variation |
IRI-2016提供的3种hmF2模型预测值可以从网站www.irimodel.org在线计算得到,也可以通过网站上提供的源代码设定hmF2的不同计算模式得到。
Jicamarca站的垂测仪每15 min进行垂直电离层探测,并记录为频高图。频高图可以由SAO-Explorer软件自动标定,hmF2可以通过该软件中的NHPC算法计算得到[9]。本文使用的自动标定的hmF2可以从网站http://giro.uml.edu/didbase/scaled.php下载。为了保证标定结果的准确度,只有信心分数为100或者人为标定的结果才会被选用,以避免低纬度地区频发的扩展F层对标定结果的干扰。
2 IRI-2016模型输出与垂测仪实测的hmF2的比较为了比较根据IRI-2016中3种hmF2模型得出的峰值高度hmF2与垂测仪观测到的峰值高度hmF2的季节性差异,本文把IRI-2016计算得到的峰值高度和实测的峰值高度按月份分为3组,即春秋季(三月、四月、九月、十月),夏季(五月至八月),冬季(一月、二月、十一月、十二月)。图 2展示的是Jicamarca站在2008年由垂测仪实测的峰值高度和由IRI-2016模型得出的3种峰值高度在不同季节随当地时间的变化。图中的峰值高度是对应季节的峰值高度的平均值,+号实线、黑实线、虚线和圈实线分别代表垂测仪观测值、CCIR模型预测值、AMTB模型预测值和Shubin模型预测值。
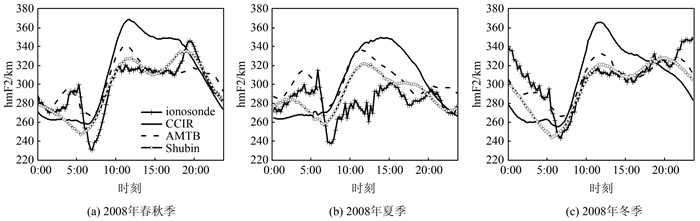 |
| 图 2 太阳活动低年(2008年),垂测仪实测的峰值高度均值与IRI 3种hmF2模型得出的峰值高度均值在不同季节的昼夜变化 Fig.2 Diurnal Variations of Ionosonde-Measured Median hmF2 and those Derived from Three hmF2 Options of IRI Model in Different Seasons During low Solar Activity Year (2008) |
由图 2可以看出,实测的峰值高度和由IRI-2016 3种hmF2模型计算的峰值高度均存在明显的季节性差异。在春秋季,垂测仪观测到的峰值高度从凌晨开始缓慢爬升,并在本地时间(local time, LT)0500时达到小高峰约300 km,之后急剧下降,在1 h左右下降至230 km。随后峰值高度上升到310 km,并在1000~1700 LT维持相对稳定。之后,进一步上升并在2000 LT达到全天的最高值然后下降。3种hmF2模型均能反映出实测峰值高度的变化趋势,但AMTB模型和Shubin模型预测值更接近实测值,而CCIR模型预测值与实测值之间存在较大的偏差,尤其是在1000~1900 LT明显高估了峰值高度。在夏季,相较于春秋季,实测的峰值高度在白天偏低。3种hmF2模型预测值与实测值之间均存在显著的差异。AMTB模型预测值绝大部分时间均高于实测值,CCIR模型和Shubin模型在日间(0700~1 900 LT)高估峰值高度而在夜间(2000~0600 LT)低估峰值高度。在冬季,全天的峰值高度的最大值出现在大约凌晨0000 LT。与其他季节不同,峰值高度在夜间0000~0500 LT出现快速的下降。Shubin模型预测值在白天和实测值非常好地吻合。AMTB模型和Shubin模型在夜间与实测值的偏差较大,而CCIR模型在夜间和正午时分(1200 LT左右)均出现较大的误差。
整体上来看,在太阳活动低年,IRI-2016中3种hmF2模型计算的峰值高度在春秋季和实测值契合度最高,冬季次之,夏季的吻合度最差。和AMTB模型和Shubin模型相比,不管在任何季节,CCIR模型的表现都比较差,并且在日间0600~1800 LT夜间,CCIR模型计算的峰值高度存在的明显高估,在夜间1900~0600 LT存在明显的低估。AMTB模型在夏季全天均高估峰值高度,并在春秋季和夏季较好地描绘出了夜间0100~0500 LT峰值高度上涨的趋势。总体上,相较于其他两种模型,Shubin模型更好地描述了真实的峰值高度变化趋势,尤其在冬季日间0700~2000 LT和垂测仪实测值非常接近。
图 3描绘的是Jicamarca站的观测值和IRI-2016中3种hmF2模型预测值在太阳活动高年(2014年)的变化情况。图中曲线表示的含义与图 2中一致。与2008年相比,峰值高度在太阳活动高年相应地增大。峰值高度在时间0600LT出现小高峰之后不断上升并在时间2000 LT左右达到全天的最大值。冬季的全天最大值明显高于夏季,并且在冬季的夜间0000~0400 LT,峰值高度快速下降,和春秋季与夏季有明显的差别。3种模型中,Shubin模型最好地描绘出了实测峰值高度的变化趋势。CCIR模型预测值仍然具有最大的偏差并且不能重现出峰值高度在夜间2 000 LT的全天最大值。CCIR模型预测值在冬季傍晚1600~0200 LT明显低于实测值。AMTB模型在春秋季和夏季几乎全天都高估峰值高度。
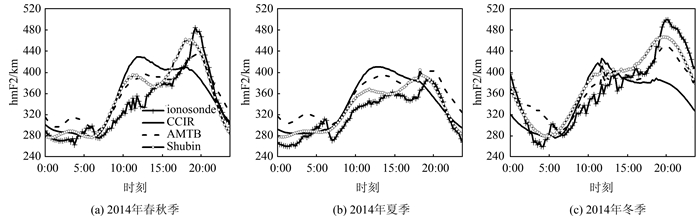 |
| 图 3 太阳活动高年(2014年),垂测仪实测的峰值高度均值与IRI 3种hmF2模型得出的峰值高度均值在不同季节的昼夜变化 Fig.3 Diurnal Variations of Ionosonde-Measured Median hmF2 and those Derived from Three hmF2 Options of IRI Model in Different Seasons During High Solar Activity Year (2014) |
为了定量分析IRI-2016 3种hmF2计算模型得出的峰值高度结果与实测值的差异,本文定义了均方根误差(RMSE)为:
| $ {\rm{RMSE}}({\rm{hmF}}{2_{{\rm{IRI}}}}) = \sqrt {\frac{{\sum\nolimits_{i = 1}^n {{{({\rm{hmF}}{2_{{\rm{IRI}}}} - {\rm{hmF}}{2_{{\rm{ion}}}})}^2}} }}{n}} $ | (2) |
式中,hmF2ion表示垂测仪测量的峰值高度;hmF2IRI表示分别由IRI-2016 3种模型计算得到的峰值高度,n为数据点总数。
图 4为太阳活动低年,IRI-2016中3种峰值高度模型的峰值高度预测值的均方根误差在不同季节的日均变化图。可以看出,在春季,3种峰值高度模型计算值与实测值的差异表现较为平稳,且均小于65 km。3种模型中,CCIR模型的误差最大,特别是在1000~1800 LT。对于Shubin模型而言,除在0500LT周围时刻,其余时间段均是3个模型中表现最为优异,在大约下午1400 LT时刻RMSE值一度低于20 km。AMTB模型在时间2000 LT附近误差较大。
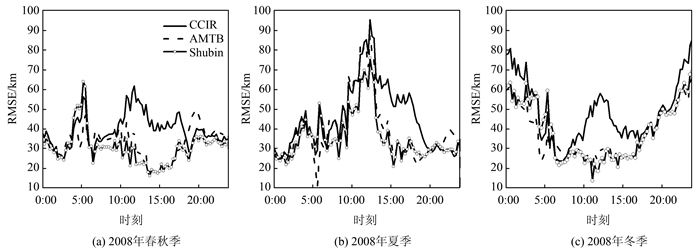 |
| 图 4 太阳活动低年(2008年),IRI 3种hmF2模型得出的峰值高度均值的均方根误差(RMSE)在不同季节的昼夜变化 Fig.4 Diurnal Variations of RMSE in Median hmF2 that Derived from Three hmF2 Options of IRI Model in Different Seasons During High Solar Activity Year (2008) |
在夏季和冬季,均方根误差RMSE均出现了剧烈的日内变化波动。夏季时,3种模型预测值在中午时段(1000~1500 LT)和实测值相比,均出现较大的误差,CCIR模型的均方根误差最大值高达95 km。误差最小的Shubin模型均方根误差也高达70 km。在冬季,AMTB模型和Shubin模型在日间(0900~1600 LT)的表现最好,均方根误差约为25 km,而CCIR模型在该时间段的误差明显高于这两个模型。而利用夜间(2100~0300 LT)3种模型的误差都急剧增大,尤其是CCIR模型在午夜0000 LT的RMSE值上升到80 km。
图 5为太阳活动高年,IRI-2016中3种峰值高度模型的峰值高度预测值的均方根误差在不同季节的日均变化图。在春秋季,3种模型预测值的RMSE呈现出“三峰两谷”的分布,即RMSE在时间0300LT,1200LT和2000LT达到峰值,在时间0600LT和1800LT达到低谷。3种模型在2014年夏季的表现最好,RMSE的数值明显低于春秋季和冬季,维持在20~65 km内波动。在冬季,CCIR模型在夜间2000~0200LT的误差最大。
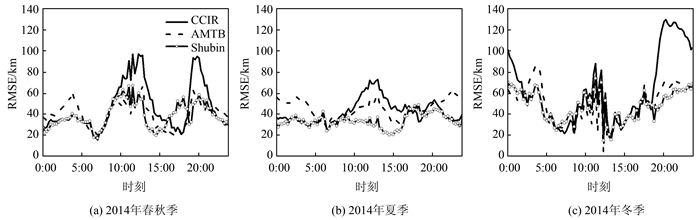 |
| 图 5 太阳活动高年(2014年),IRI 3种hmF2模型得出的峰值高度均值的均方根误差(RMSE)在不同季节的昼夜变化 Fig.5 Diurnal Variations of RMSE in Median hmF2 that Derived from Three hmF2 Options of IRI Model in Different Seasons During High Solar Activity Year (2014) |
随着太阳活动强度的增大,峰值高度逐渐升高,3种模型预测值的误差也逐渐增加(夏季除外)。与文献[10]中使用的中国区域的4个垂测仪站的比较结果相比,IRI-2016的3种模型在磁赤道地区的误差较大。与其他两种模型相比,CCIR模型在不同下午太阳活动水平和不同季节条件下和垂测仪实测结果有明显的偏差,表明CCIR模型在磁赤道地区表现欠佳。一方面是由于使用式(1)计算带来不确定性;另一方面,建模时使用的系数阶数太低使其无法重现日变化中的小尺度特征。此外,CCIR模型在极端低太阳活动水平时,如2008年,不能产生真实的hmF2值,也是导致其偏差特别大的原因之一[11-13]。总体来看,Shubin模型相对表现最佳。Shubin模型综合使用了地基垂测仪数据和天基掩星数据(CHAMP, GRACE, COSMIC)来建模,并且建模时采用的数据涵盖低太阳活动水平时段。天基掩星数据部分弥补了仅依靠垂测仪数据建模带来的误差,结果比仅靠垂测仪数据的AMTB模型精度更高,尤其是对CCIR模型的精度有了大幅度地提高。
3 结束语本文使用了Jicamarca站的垂测仪观测数据对IRI-2016 3种峰值高度计算模型在不同太阳活动水平条件下磁赤道地区的性能进行了评估,结果发现3种IRI-2016峰值高度模型的表现存在明显的季节特征,在太阳活动低年,3种模型在春秋季的表现优于夏季和冬季,在太阳活动高年,3种模型在夏季的表现由于春秋季和冬季。3种模型计算的hmF2预测值在日间(0700~1900LT)均普遍高于实测值,CCIR模型和Shubin模型预测值在夜间(2000~0600LT)大部分低于实测值。3种模型中,CCIR模型表现最差。综合来看,在磁赤道地区,本文推荐使用Shubin模型来对电离层峰值高度进行估计。
| [1] |
Gordiyenko G I, Yakovets A F. Comparison of Midlatitude Ionospheric F Region Peak Parameters and TopsideNe Profiles from IRI2012 Model Prediction with Ground-Based Ionosonde and Alouette Ⅱ Observations[J]. Advances in Space Research, 2017, 60(2): 461-474. DOI:10.1016/j.asr.2017.01.006 |
| [2] |
韩吉德, 王祖顺, 王春青. 全球电离层时空变化特性分析[J]. 测绘地理信息, 2012, 37(6): 26-29. |
| [3] |
Bilitza D, Altadill D, Truhlik V, et al. International Reference Ionosphere 2016: From Ionospheric Climate to Real-Time Weather Predictions[J]. Space Weather, 2017, 15(2): 418-429. DOI:10.1002/2016SW001593 |
| [4] |
黄智, 袁洪. 磁赤道地区2007-2013年COSMIC掩星反演和国际参考电离层模型输出结果分析[J]. 地球物理学报, 2016, 59(7): 2333-2343. |
| [5] |
Zhang MianLian, Liu Libo, Wan Weixing, et al. An Update Global Model of hmF2 from Values Estimated from Ionosonde and COSMIC/FORMOSAT-3 Radio Occultation[J]. Advances in Space Research, 2014, 53(3): 395-402. DOI:10.1016/j.asr.2013.11.053 |
| [6] |
Altadill D, Magdaleno S, Torta J M, et al. Global Empirical Models of the Density Peak Height and of the Equivalent Scale Height for Quiet Conditions[J]. Advances in Space Research, 2013, 52(10): 1756-1769. DOI:10.1016/j.asr.2012.11.018 |
| [7] |
Shubin V N. Global Median Model of the F2-Layer Peak Height Based on Ionospheric Radio-Occultation and Ground-Based Digisonde Observations[J]. Advances in Space Research, 2015, 56(5): 916-928. DOI:10.1016/j.asr.2015.05.029 |
| [8] |
Bilitza D, Altadill D, Zhang Y L, et al. The International Reference Ionosphere 2012—A Model of International Collaboration[J]. Journal of Space Weather and Space Climate, 2014, 4(A07). DOI:10.1051/SWSC/2014004 |
| [9] |
Huang Xueqin, Reinisch B W. Vertical Electron Density Profiles from the Digisonde Network[J]. Advances in Space Research, 1996, 18(6): 121-129. DOI:10.1016/0273-1177(95)00912-4 |
| [10] |
Zhao Xiukuan, Ning Baiqi, Zhang Manlian, et al. Comparison of the Ionospheric F-2 Peak Height Between Ionosonde Measurements and IRI2016 Predictions over China[J]. Advances in Space Research, 2017, 60(7): 1524-1531. DOI:10.1016/j.asr.2017.06.056 |
| [11] |
Hoque M M, Jakowski N. A New Global Model for the Ionospheric F2 Peak Height for Radio Wave Propa gation[J]. Annales Geophysicae, 2012, 30(5): 797-809. DOI:10.5194/angeo-30-797-2012 |
| [12] |
Shubin V N. Global Median Model of the F2-Layer Peak Height Based on Ionospheric Radio-Occultation and Ground-Based Digisonde Observations[J]. Advances in Space Research, 2015, 56(5): 916-928. DOI:10.1016/j.asr.2015.05.029 |
| [13] |
Mutch S J, Poole G B, Croton D J. Constraining the last 7 Billion Years of Galaxy Evolution in Semi-analytic Models[J]. Monthly Notices of the Royal Astronomical Society, 2013, 428(3): 2001-2016. DOI:10.1093/mnras/sts182 |
 2019, Vol. 44
2019, Vol. 44


