| 无验潮水深测量测深精度分析及检验 |
2. 中国海警局直属第三局,广东 广州,520320;
3. 中国电建集团青海省电力设计院有限公司,青海 西宁,810008
2. The Third Bureau directly under China Coast Guard, Guangzhou 520320, China;
3. Power China Qinghai Electric Power Design Institute Co., Ltd., Xining 810008, China
随着RTK(real-time kinematic)测高精度提高且可靠性得到保证,利用实时的接收机三维坐标,结合测深设备能够直接推算出实时水下高程,即无验潮水深测量方法随之而生。RTK技术自动化程度高,能够全天候不间断地作业,大大减少了测量人员的劳动强度。20世纪末,德国联邦海事局和汉诺威大学大地研究院合作,对利用GPS大地高信息进行水深归算进行了试验论证,成果分析表明DGPS(differential-GPS)/OTF技术能够提供很好的测高精度,不受水位、吃水、涌浪影响的实时水深改正将成为可能。桑金[1]在国内较早地采用了GPS大地高的信息进行水深改正,认为这是一种实时的、与动吃水无关的、无验潮站的水位改正方法,可认为是我国无验潮水下地形测量的初步探索。李凯锋等[2]利用无验潮水深测量系统定位设备,采集了静态和动态两组定位数据,从静态和动态定位两个方面分析了不同长度基线的解算结果。结果表明:基线长度在40 km范围以内,定位结果完全满足测量精度要求。随着GNSS定位精度的提高,以及CORS等技术带来的操作便利,无验潮测水深技术也得到了大规模的拓展,应用更加广泛[3-9]。
1 两种水深测量方式的原理 1.1 验潮水深测量原理测船上由RTK技术实时获得接收机的平面位置(x,y),由测深仪测出换能器与水底间垂直距离S,验潮人员定期观察记录水位值H验潮,内业处理,结合换能器吃水h,推算出各个水底定位点的高程,如图 1所示。
| $ {H_{水底}} = {H_{验潮}} - h - S $ | (1) |
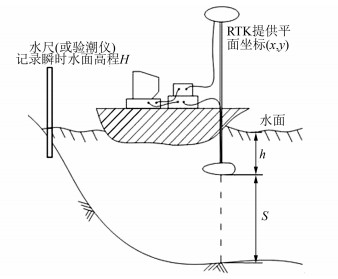 |
| 图 1 验潮水深测量示意图 Fig.1 Non-Tidal Observation Survey Method Diagram |
1.2 无验潮水深测量原理
联测带有潮位高程基准的高程点,将RTK给出的大地高改正至和潮位高程基准,而后,通过RTK技术直接获的接收机天线中心的三维坐标(x,y,H),测深仪同步给出换能器与水底的距离S,结合测杆长度L,直接获取水底定位点的高程,如图 2所示。
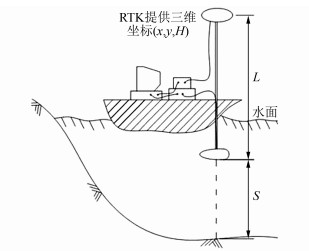 |
| 图 2 无验潮水深测量示意图 Fig.2 Tidal Observation Survey Method Diagram |
理想情况下,水底深度实时获得,几乎不需要后处理工作。
| $ {H_{水底}} = {H_{接收中心}} - L - S $ | (2) |
顾及测船姿态因素的影响,式(2)中的测杆长度L需换算至GNSS天线中心到换能器之间的真实垂直距离,换能器至水底的距离S也要换算至水底点垂直至水面的距离,同时更新测深记录点的平面位置,相应内容在§2. 2节进行论述。
在大面积水域(海洋)测量中,由于上下游水位存在坡降比,大面积测量范围还存在高程异常不均匀的情况,往往需要在水域测区内分设几处验潮点,不仅费时费力,而且在复杂海域并不易实现,此时无验潮方法显示出其独特的优越性。
2 无验潮水深测量精度分析无验潮水深测量的精度受到测深系统安装、测船姿态、测区高程异常等方面影响。
2.1 水深测量系统安装的影响根据水底高程计算式(2),测深精度包括测深仪测深精度MS、接收机天线至换能器零点的测量精度ML,以及RTK获取高程的测量精度MRTK3个方面,见式(3)。
| $ {M_{H水底}} = \pm \sqrt {{M_S}^2 + {M_L}^2 + {M_{RTK}}^2} $ | (3) |
工程测量规范[10]中对测深点的深度中误差的要求如表 1所示。
| 表 1 测深点深度中误差 Tab.1 Sounding Point Depth Mean Square Error |
 |
基于RTK的技术特点,其成果精度存在距离效应,因此在实际操作中要控制好作业范围,必要时可多次架设基站。考虑较差情况,取接收机中心高程精度为MRTK = ±8 cm(实际测量中可达±5 cm以内);使用精度±1 mm的钢尺量取连接杆的长度,取3次均值为结果,则ML = ±0. 6 mm;根据经验,中海达单波速测深仪在水深45 m左右水域进行测量时,实测偏差可达到4 cm,而且深度越大测量精度越低,取最不利情况下的测量精度MS = ±10 cm。可计算出水底点高程精度MH水底 = ±12. 8 cm,能够满足表 1的要求。
2.2 测船姿态的影响在实践中,测船姿态对高程的精度有较大的影响。如图 3所示,在船体发生晃动时,虽然RTK能够获得较好的水平位置精度,但此时RTK反馈在成果中的平面位置O对应的水底D点,与测深仪实际探测的水下高程点D’点并不一致,造成高程误差Δ = OD- OD'。
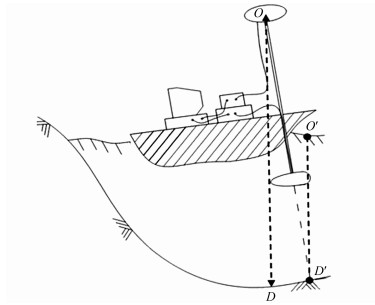 |
| 图 3 测船倾斜造成高程测量误差示意图 Fig.3 Elevation Errors Cause by Inclination |
事实上,换能器杆安装偏差与测船倾斜造成影响是一致的,文献[11]指出,该类误差属于偶然误差,在单波速测量时,测船倾斜的影响与换能器杆的安装偏差可一并考虑。
值得注意的是,当DD'位于陡坡,或船体倾角较大时,通过图 3,可以直观地看出,产生的高程误差将是非常可观的,必须加以考虑。针对此,需要避开可能造成测船姿态差的恶劣测量环境,在测船上加装姿态测定仪将高差改正为Δh = OD' cos α,再根据水平方向的两个姿态角β,γ将定位点由O改正至O′。
2.3 测区高程异常的影响水域测量图的图载水深普遍采用当地理论最低潮面为深度基准面[12]。当地理论最低潮面常取在当地多年平均海面下一定深度l位置,RTK高程基准的参考椭球面,与前述平均海面之间存在一个差值,即高程异常Δ,通过l值和Δ值,能够将RTK高程改正至深度基准面中来。一般认为在同一区域l值为一固定值。高程异常Δ需要在实地联测水准点加以检验,当测区较小时,可认为Δ为一固定数值;当测区较大时,考虑高程异常分布不均匀的情况,需要进行似大地水准面精化,求取测区Δ模型。当水下测图需求为独立高程系统时,可不考虑此项。
3 精度检验基于海南省某海岸水域水下地形测量实例,对无验潮水深测量的高程精度进行统计检验。测区顺海岸方向2. 5 km,至海岸线起往海方向0. 45 km,使用中海达HD-370单波束测深仪结合GNSS RTK技术进行测量,在无验潮水深测量的同时,也进行验潮工作,最后得到两套成果,即无验潮水下地形成果和验潮水下地形成果。
3.1 无验潮水深测量精度在测深作业的各个深度级水域将仪器推算的水深与水坨测值比对,实测水底高程精度能够满足表 1的要求。比较检查线与测深线交叉处水底高程值,检查线基本垂直于主测深线,总长度大于主测线长度的5%,检查线与主测线相交处图上1 mm范围内水深点,高程差值基本在0. 1 m以内,最大差值为0. 15 m,如表 2所示。
| 表 2 检查线统计表 Tab.2 Test Line Statistical Table |
 |
3.2 无验潮成果与验潮成果比较
假定验潮测量成果为“真值”,对两套成果中的4 111个同名测深点高程进行比对分析,如表 3所示。
| 表 3 无验潮与验潮水底高程(绝对值)差值分布表/m Tab.3 Elevation Difference(Absolute Value)Distribution Table Between Non-Tidal and Tidal Observation Survey Method/m |
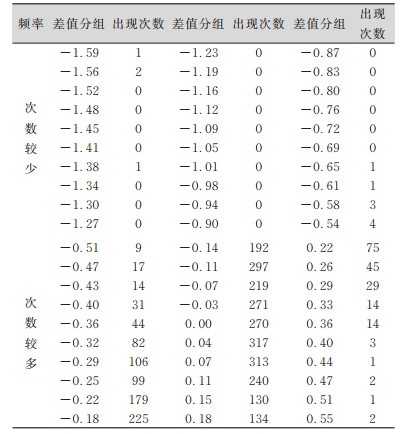 |
通过表 3可以看出,绝对值差值在(-1. 6,-0. 7)区间出现次数极少,仅4次,不足样本总数的0. 1%,认定其为粗差予以剔除。出现次数较多的区间差值绝对值绝大部分集中在0附近,即两套成果值相当。分析各分段差值出现的次数,可以看出,这些差值服从高斯正态分布,经过计算,其服从一个数学期望μ =0,方差σ2=0. 013的正态分布N(0,0. 013),即差值的分布具有集中性、对称性、均匀变动性。如图 4所示。
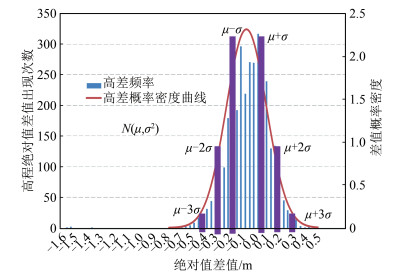 |
| 图 4 无验潮与验潮水底高程(绝对值)差值概率曲线图 Fig.4 Elevation Difference(Absolute Value)Probability Curve Between Non⁃Tidal and Tidal Observation Survey Method |
根据表 3和图 4分析,可以从以下两个方面说明无验潮与验潮水底高程值之间的关系。
1)根据正态分布的特点,标准差σ越小,分布越集中在μ附近,σ=1为标准正态分布,本案例中σ= 0. 12,表示两套高程值绝对值差值较集中于0,即两套值的4 000余样本整体较为接近。
2)将图 4中曲线及坐标轴截图插入AutoCAD软件,求取封闭面积的值。假设概率分布曲线与横轴所围面积为S,μ ± σ所围面积为S×67. 9%,μ ± 2σ所围面积为S× 93. 6%,μ ± 3σ所围面积为S× 99. 2%,与正态曲线对应的68. 3%、95. 5% 和99. 7% 基本一致,支持了两套样本基本一致的判断。
4 结束语鉴于全球导航卫星系统星空组网的特点,在某些特定区域,RTK获取的三维坐标精度仍不够高,尤其是高程精度[5, 11]。同时,在对海域进行水下地形测量时,由于大海是开放式的,缺少等级水准点,利用陆上的高程控制点进行高程异常拟合只能采用外推的方法,离岸距离越远,精度越低。此时还是需要进行验潮式的水深测量,或通过验潮来提高高程异常拟合的精度[13, 14]。
当测量条件适宜时,无验潮水深测量的测深精度能够满足测深精度要求,而且成果与验潮式的成果相当,效率高、用工省,经济效益好,值得在进行水下地形测量中探索使用。
| [1] |
桑金. 基于GPS技术的水深归算法[J]. 测绘通报, 1999(8): 23-25. |
| [2] |
李凯锋, 田建波, 赵树红, 等. 无验潮水深测量系统定位精度检验[J]. 海洋测绘, 2013, 33(6): 22-25. |
| [3] |
张国利, 时小飞, 杨开伟, 等. 网络RTK支持下的无验潮水深测量方法及其应用[J]. 测绘通报, 2016(12): 140-141. |
| [4] |
陈希. RTK-GPS技术在水下地形测量中的应用[J]. 中国水运(下半月刊), 2010, 10(11): 65-66. |
| [5] |
肖国磊, 朱伟荣. RTK技术在水下地形测量中的应用初探[C]. 上海市岩土工程检测中心论文集(1995- 2005), 上海: 同济大学电子音像出版社, 1995
|
| [6] |
魏荣灏, 陈佳兵, 徐达. 基于PPK无验潮的水下地形测量技术研究[J]. 海洋技术学报, 2021(1): 57-62. |
| [7] |
袁正午, 何格格. 一种高精度的GPS-RTK定位技术设计与实现[J]. 电子技术应用, 2018(6): 63-67. |
| [8] |
孙斌, 孟庆鹏. 无验潮测深技术在海洋测绘中的应用[J]. 经纬天地, 2018(1): 57-60. |
| [9] |
刘昊. 城市测量中网络RTK技术的应用研究[J]. 技术与市场, 2019(3): 169. |
| [10] |
中国有色金属工业协会. 工程测量规范: GB 50026- 2007[S]. 北京: 中国计划出版社, 2008
|
| [11] |
卢军民, 安延云, 张东明, 等. 无验潮测深技术中影响水深测量精度的几个问题探讨[J]. 水运工程, 2010(5): 47-51. |
| [12] |
尹亚娟, 张朝阳, 高德俊. 岛礁近海水下高程改正方法初探[J]. 测绘地理信息, 2017, 42(1): 34-37. |
| [13] |
张胜凯, 朱朝辉, 肖峰, 等. 利用IceBridge测高数据计算海冰干舷的方法研究[J]. 测绘地理信息, 2019, 44(3): 21-27. |
| [14] |
孙新轩, 佟杰, 李磊. 多波束水深数据不确定度研究[J]. 测绘地理信息, 2019, 44(6): 48-50. |
 2022, Vol. 47
2022, Vol. 47

