| 侧扫声呐条带数据处理及其无缝成图 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079;
3. 武汉大学动机学院,湖北 武汉,430072
2. Key Laboratory of Precise Engineering & Industry Surveying, NASG, Wuhan 430079, China;
3. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
海床地貌图像作为海洋数字化工作中最常见的数据源之一,其处理精度和质量对能否准确描述海床表面特征至关重要。目前,海底地貌图像主要通过侧扫声呐系统采集时序信号获得,受其测量原理及作业模式制约,侧扫声呐图像多以瀑布图像形式存在。由于缺乏直观、准确的方向、位置信息,侧扫声呐瀑布图像的准确判读需要丰富的人工经验,并且仅能进行水下目标的定性分析[1]。瀑布图像的上述不足,限制了其与其他空间数据的融合及使用范围。
针对侧扫声呐瀑布图像存在的辐射畸变、倾斜几何畸变、压缩畸变、使用不直观等问题,国外已出现SonarWeb、Triton等侧扫声呐数据综合性处理软件,但仍然存在水柱区域未改正、编码图像缝隙未填补等问题[2, 3];国内学者在此领域的工作主要集中在原始数据解码及格式统一[4]、海底线提取[5]、地理编码[6]、图像增强[7-9]等,相关研究大都针对侧扫声呐图像处理一个或部分方面进行研究,系统性、综合性的研究相对较少。本文从侧扫声呐诸畸变产生机理入手,对瀑布图像处理的关键环节进行探讨和研究,以期形成一套完善了侧扫声呐条带数据处理及无缝成图方法。
1 侧扫声呐瀑布图像处理原始侧扫声呐瀑布图像不同于普通的光学成像,如图 1所示。在海底第一个回波返回之前,换能器仅能接收到水体噪声,图像中间形成弱回波水柱区域;由于采用等时间斜距记录模式,图像存在倾斜几何畸变;受声能扩展损失、吸收损失影响,图像横向上存在辐射畸变;受船速变化影响,图像纵向上存在压缩畸变。由于不具备直观的坐标信息,瀑布图像使用极不方便,难以与其他地理信息数据进行有效融合。
侧扫声呐瀑布图像的处理主要包括海底追踪、灰度增益、斜距改正等内容。
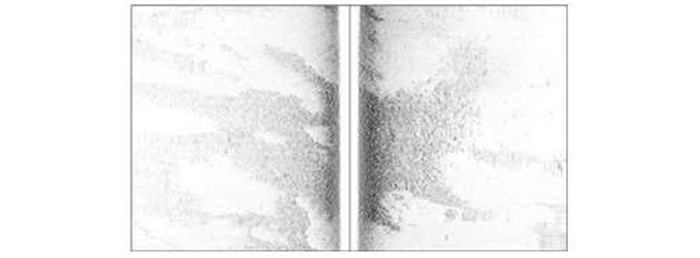 |
| 图 1 侧扫声呐原始数据形成的瀑布图像 Figure 1 Waterfall Image Formed by Side-scan Sonar Raw Data |
1.1 海底追踪
海底线由每Ping扫描线中第一个海底强回波序列组成,它表征了拖鱼至海底的高度变化,既是侧扫声呐横向增益的起始线,也是斜距改正的基准线,正确提取海底线是瀑布图像后续处理的基础。声波由水体传播至海底,回波信号会发生阶跃变化,因此,可以通过设置合适的阈值T(见图 2),按接收时间先后顺序,在回波序列中寻找首个强度In>T的回波,认为该回波即为海底表面的第一个回波,该回波至拖鱼的距离即为拖鱼到海底的高度。
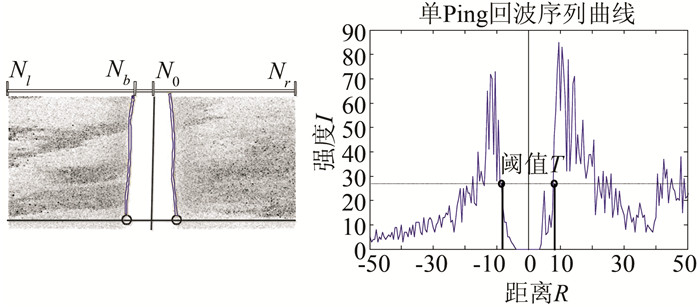 |
| 图 2 阈值法提取海底线示意图 Figure 2 Sketch Map for Sea Bottom Tracking by Threshold Method |
1.2 灰度增益
侧扫声呐图像的辐射畸变主要表现为横向上的灰度不均衡。侧扫声呐图像的灰度增益常依据经验公式对传播损失进行补偿,见式 (1)。
| $ TL=n\cdot 10\log R+\alpha R $ | (1) |
式中,系数n与波束形状有关;吸收系数α与声波的发射频率、海水温度及盐度等有关系。
1.3 斜距改正受斜距记录影响,侧扫声呐图像横向上存在倾斜几何畸变;水柱的存在也导致拖鱼正下方目标被分离在两侧,因此,需要对侧扫声呐图像进行斜距改正,得到各回波的平距。
图 3为瀑布图像的某Ping回波,N为每侧回波总采样个数,nh为海底线至发射线的斜距像素宽度,ni为当前回波至发射线的斜距像素宽度,当海底地形变化平缓时,各回波至海底线的平距像素宽度为:
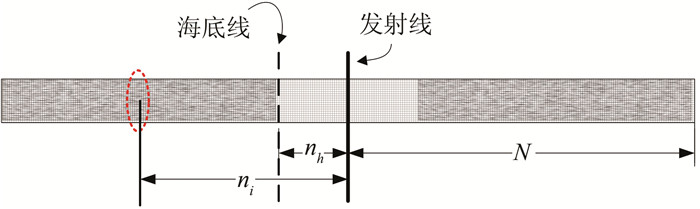 |
| 图 3 回波、海底线、拖鱼的位置关系 Figure 3 Spatial Relationship of Echo, Sea Bottom and Tow-fish |
| $ {{{n}'}_{i}}=\sqrt{n_{i}^{2}-n_{h}^{2}} $ | (2) |
拖鱼常与绞架的拖点相连,GPS和姿态传感器安装在船上 (见图 4),拖鱼的瞬时位置可由拖点的位置结合航向A和拖缆长度L进行估算,而拖点实时位置需结合GNSS导航数据和船体姿态数据通过坐标旋转得到[10]。
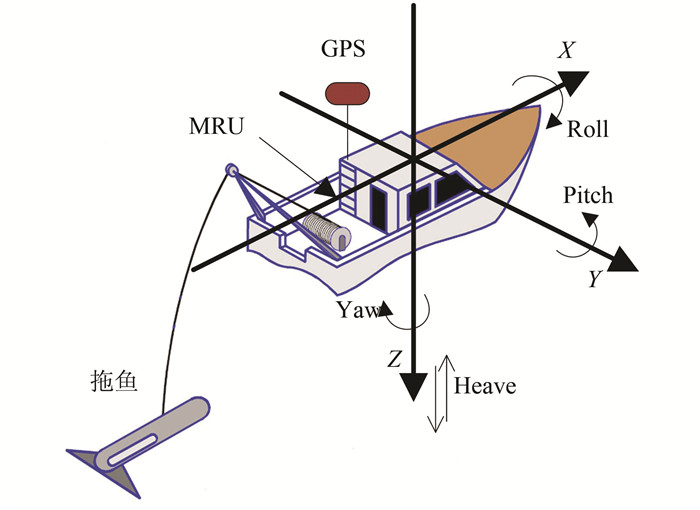 |
| 图 4 船体坐标系统VFS Figure 4 Vessel Frame System |
2.1 拖点瞬时坐标求解
静止状态下,拖挂点的船体坐标为 (x, y, z)VFS-T0,GPS的船体坐标为 (x, y, z)VFS-GPS0,GPS实时测量值为 (X,Y,Z)GRF-GPS,行驶航向为A,受船体姿态影响 (roll (r),pitch (p)),拖挂点的实时地理坐标为 (x, y, z)GRF-T:
| $ {{\left( \begin{matrix} \Delta x \\ \Delta y \\ \end{matrix} \right)}_{\rm{VFS-T-GPS}}}=\mathit{\boldsymbol{R}}(p)\mathit{\boldsymbol{R}}(r)\bullet \left[{{\left( \begin{matrix} x \\ y \\ \end{matrix} \right)}_{\rm{VFS-T0}}}-{{\left( \begin{matrix} x \\ y \\ \end{matrix} \right)}_{\rm{VFS-GPS0}}} \right] $ | (3) |
| $ {{\left( \begin{matrix} X \\ Y \\ \end{matrix} \right)}_{\rm{GRF-T}}}={{\left( \begin{matrix} X \\ Y \\ \end{matrix} \right)}_{\rm{GRF-GPS}}}+\mathit{\boldsymbol{R}}(A){{\left( \begin{matrix} \Delta x \\ \Delta y \\ \end{matrix} \right)}_{\rm{VFS-T-GPS}}} $ | (4) |
式中,
拖鱼位置一般通过拖缆长度近似计算,缆线一般都有较好的强度和柔性,在拖曳过程中,拖缆很大程度上减弱了船体姿态变化对拖鱼的影响。因此,当船匀速直线航行时,可以认为拖鱼仅受向前的牵引力,拖缆由于自重,三角形的斜边常取拖缆长度L的0.9倍,拖鱼至拖点的水平距离按图 5中三角形的几何关系推算。
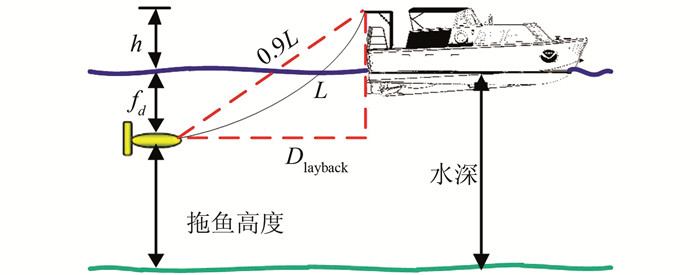 |
| 图 5 拖鱼瞬时位置的推算 Figure 5 Sketch Map for Calculating Instantaneous Location of Tow-fish |
| $ {{D}_{\text{layback}}}=\sqrt{{{(0.9L)}^{2}}-{{(h+{{f}_{d}})}^{2}}} $ | (5) |
式中,h为绞架至水面的高度;fd为拖鱼至水面的距离,该值可由压力传感器求得。最后,由拖鱼与船体的航向一致性,通过拖点位置可求出拖鱼地理坐标为:
| $ {{\left( \begin{matrix} x \\ y \\ \end{matrix} \right)}_{\text{VFS }\!\!\_\!\!\text{ TOW}}}={{\left( \begin{matrix} x \\ y \\ \end{matrix} \right)}_{\text{GRF }\!\!\_\!\!\text{ T}}}+\left( \begin{matrix} {{D}_{\text{layback}}}\bullet \cos (A+\pi ) \\ {{D}_{\text{layback}}}\bullet \sin (A+\pi ) \\ \end{matrix} \right) $ | (6) |
如图 6所示,每Ping回波测量时, 拖鱼正下方投影点的地理坐标为P0(X0,Y0),侧扫声呐单侧扫幅为R,每个通道的采样率为N,航向为α,由于每Ping回波垂直于航向,因此,左舷通道回波的方位角θ=α-π/2,右舷通道回波的方位角则为θ=α+π/2,Pi为某通道的第i个回波,则Pi的地理坐标 (Xi, Yi) 为:
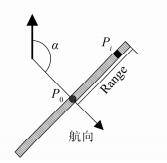 |
| 图 6 回波位置计算示意图 Figure 6 Sketch Map for Calculating Echo Position |
| $ \left\{ \begin{align} & {{X}_{i}}={{X}_{0}}+R\bullet \cos (\alpha \pm {\pi }/{2}\;)\bullet i/N \\ & {{Y}_{i}}={{Y}_{0}}+R\bullet \sin (\alpha \pm {\pi }/{2}\;)\bullet i/N \\ \end{align} \right. $ | (7) |
当每个回波的地理坐标确定以后,便可以获得条带声呐图像的实际地理范围 (Xmin, Ymin;Xmax, Ymax)。根据设定的像素尺寸Δd,求得图像的分辨率以及点Pi (Xi, Yi) 对应的像素坐标pi(xi, yi) 为:
| $ \left\{ \begin{matrix} {{x}_{i}}=({{X}_{i}}-{{X}_{\min }})/\Delta d \\ {{y}_{i}}=({{Y}_{i}}-{{Y}_{\min }})/\Delta d \\ \end{matrix} \right. $ | (8) |
计算侧扫声呐每一个回波的像素坐标,并根据回波强度确定对应的像素值,从而得到如图 7的侧扫声呐瀑布图像。
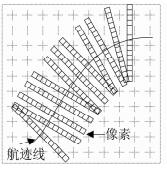 |
| 图 7 瀑布图像地理编码示意图 Figure 7 Sketch Map for Geocoding of Waterfall Image |
3.2 缝隙填补采样
当拖鱼航向发生变化时,扫描线的边缘产生缝隙,缝隙填补的关键是如何确定填充区域。基于侧扫声波发射原理和计算机图形原理,本文给出了扇形法和扫描法两种填充方法。
扇形填充法符合侧扫声呐发射声波照射机理,发射波束具有一定的角度,整个海底的照射区域近似于扇形,如图 8所示。因此可根据侧扫声呐发射波束的角度,结合横向距离,计算出每个回波代表的实际纵向高度。图 8中,Ha=R·θ,以a点为中心,纵向上Ha宽度内所有的像素点的像素值应该与a点相同,利用这种方法可以实现扫描线边缘的缝隙填补。当拖鱼航向变化缓慢时,扫描线边缘缝隙较小,扇形填充法可以取得较好的效果。
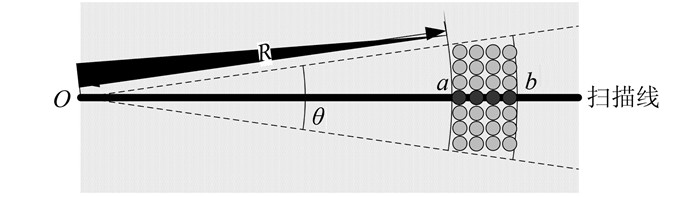 |
| 图 8 侧扫声呐地理编码图像缝隙的扇形填充法 Figure 8 Gap Filling in Side-scan Sonar Geocoding Image by Sector Method |
扫描填充法是计算机图形学中常见的区域填充算法,可实现对任意封闭区域的填充。在相邻两Ping扫描线上选取距离最近的4个点,如图 9所示,A1、A2为同一扫描线上的相邻两个回波,B3、B4为邻近扫描线上的两个相邻点,A1、A2、B3、B4组成一个闭合的连通区域,采用扫描填充法,可以标定区域内部所有的像素点,每个像素点的像素值可由式 (9) 按反距离加权法求得。扫描填充法运算量较大,但在航向快速变化的低采样区域仍可实现无缝填充,适用范围较广。
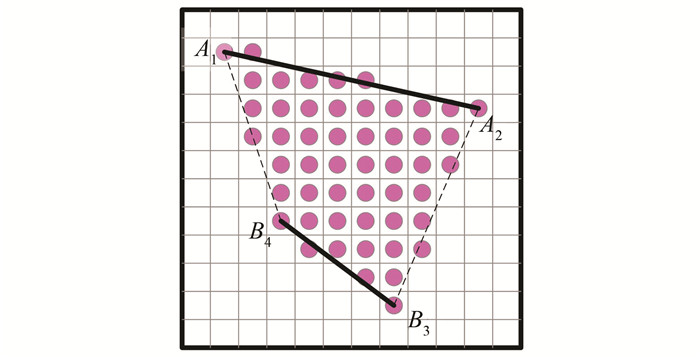 |
| 图 9 侧扫声呐地理编码图像的扫描填充法 Figure 9 Gap Filling in Side-scan Sonar Geocoding Image by Scanning Method |
| $ \text{I=}{\left( \frac{1}{{{\text{s}}_{1}}}{{\text{I}}_{{{\text{A}}_{1}}}}\text{+}\frac{1}{{{\text{s}}_{2}}}{{\text{I}}_{{{\text{A}}_{2}}}}\text{+}\frac{1}{{{\text{s}}_{3}}}{{\text{I}}_{{{\text{B}}_{3}}}}\text{+}\frac{1}{{{\text{s}}_{4}}}{{\text{I}}_{{{\text{B}}_{4}}}} \right)}/{\sum\limits_{i=1}^{4}{\frac{1}{{{\text{s}}_{\text{i}}}}}}\; $ | (9) |
本文在深圳以南某水域进行了侧扫声呐数据采集,船上配有GPS接收机、MRU及罗经等设备,拖揽长度为5 m,测区水深为8~12 m,数据记录格式为XTF格式,测区海床以泥沙和礁石为主要底质,海床目标特征丰富。选取其中一个条带数据作为试验对象,所选条带数据的相关参数如表 1所示。
| 表 1 侧扫声呐条带数据相关参数 Table 1 Main Parameters of Side-scan Sonar Data |
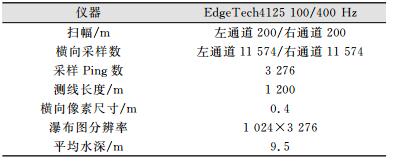 |
对原始XTF数据解码,提取导航、罗经、姿态数据并进行质量控制,提取左右通道回波数据,按脉冲发射先后纵向堆叠,形成侧扫声呐瀑布图像,按阈值法对原始瀑布图像进行海底追踪,可提取水柱两侧的海底线,如图 10所示。
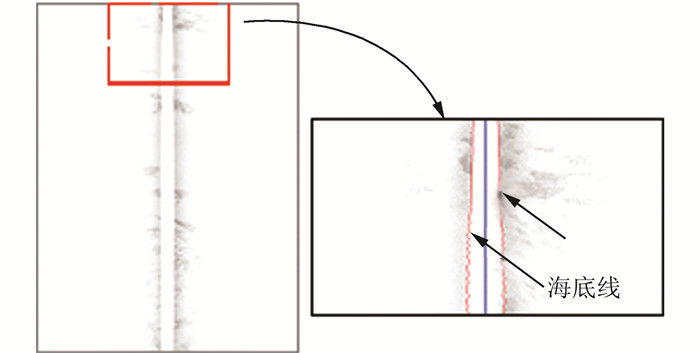 |
| 图 10 原始瀑布图像及海底追踪 Figure 10 Raw Waterfall Image and Sea Bottom Tracking |
以海底线为起算基准,对瀑布图像进行时变增益,调整式 (1) 中参数n和ɑ,直到瀑布图像边缘和中间的灰度均衡,然后按式 (2) 对增益后的瀑布图像进行斜距改正,斜距改正后,图像横向倾斜几何畸变得到改善,如图 11所示。
 |
| 图 11 瀑布图像的灰度增益及斜距改正 Figure 11 Radiation Correction and Slant-range Correction of Waterfall Image |
因受拖鱼航向变化的影响,归位计算后扫描线边缘出现交叉和缝隙 (图 12(a)),导致海床目标轮廓缺失,判读困难,而采用扫描填充法对扫描线边缘进行重采样处理,从图 12(b)可以看出,最终得到了一幅削弱了辐射畸变、倾斜几何畸变、压缩畸变影响、灰度均衡和目标轮廓清晰的无缝地理编码图像,成图质量优于SonarWeb商用软件 (见图 12(c))。
 |
| 图 12 侧扫声呐地理编码图像缝隙填补实例 Figure 12 An Example of Gap Filling in Side-scan Sonar Geocoding Image |
5 结束语
本文针对侧扫声呐瀑布图像成图质量不高、使用不直观等问题,对侧扫声呐条带数据处理的各个环节开展了系统研究,形成了一套集海底追踪、斜距改正、拖鱼归位计算、地理编码、缝隙填补等技术为一体的侧扫声呐条带数据处理及无缝成图方法。试验结果表明,经过深加工后的侧扫声呐地貌图像,不仅较好地消除了各种畸变的影响,而且灰度均衡、目标轮廓清晰,具有直观的坐标信息,极易与其他地理信息数据融合,对开展更深入的定量分析工作具有重要的意义。
| [1] | Blondel P. The Handbook of Sidescan Sonar[M]. Heidelberg, Berlin: Springer, 2010. |
| [2] | Chavez P S, Isbrecht J, Galanis P, et al. Processing, Mosaicking and Management of the Monterey Bay Digital Sidescan-sonar Images[J]. Marine Geology, 2002, 181(1): 305–315. |
| [3] | Chang Y C, Hsu S K, Tsai C H. Sidescan Sonar Image Processing: Correcting Brightness Variation and Patching Gaps[J]. Journal of Marine Science and Technology, 2010, 18(6): 785–789. |
| [4] | 韩春花, 殷汝广, 张俊明, 等. XTF格式侧扫声纳数据格式解析与应用[J]. 海洋信息, 2012, (1): 17–21. |
| [5] | 张济博, 潘国富, 丁维凤. 基于LOG算子的侧扫声呐海底线检测[J]. 海洋通报, 2010, 29(3): 324–328. |
| [6] | 邓雪清, 巩丹超, 罗睿. 侧扫声纳图像地理编码技术研究[J]. 海洋测绘, 2002, 22(4): 14–17. |
| [7] | 滕惠忠, 严晓明, 李胜全, 等. 侧扫声纳图像增强技术[J]. 海洋测绘, 2004, 24(2): 47–49. |
| [8] | 李海滨, 滕惠忠, 宋海英, 等. 小波函数对侧扫声纳图像滤波效果的影响分析[J]. 海洋测绘, 2009, 29(3): 65–67. |
| [9] | 盛惠兴, 孟凡玲, 李庆武, 等. Curvelet变换域侧扫声纳图像增强算法[J]. 海洋测绘, 2012, 32(1): 8–10. |
| [10] | 赵建虎, 刘经南. 多波束测深及图像数据处理[M]. 武汉: 武汉大学出版社, 2008. |
 2017, Vol. 42
2017, Vol. 42

