| 利用高程补偿法的高速铁路坐标系建立 |
2. 广州市城市规划勘测设计研究院, 广东 广州,510060
2. Guangzhou Urban Planning Survey Design and Research Institute, Guangzhou 510060, China
为了满足高铁轨道的平顺性,必须建立一套适合于勘测、施工、运营维护的控制测量体系,这对工程测量的精度提出了很高的要求[1]。在高铁实际施工中,要求由坐标反算的边长值与现场实测值应保持一致,其中文献[2]要求把边长投影变形值控制在不大于10 mm/km,以满足客运专线轨道施工测量的要求[3]。这样就必须要建立合适的工程坐标系来达到相应的要求。
目前,传统建立独立坐标系的过程为:首先根据测区平均高程面构建一个工程椭球,然后按照某一投影模型按等角投影方式将椭球面元素投影至平面[4, 5]。事实上,在目前已建成的高铁线路中,大多数都是采用基于平均高程面的任意带高斯投影方式来建立工程坐标系[6, 7],其中也有部分线路采用了斜墨卡托投影和兰勃特投影方式来建立坐标系[8]。因此,研究高铁中如何建立合适的工程坐标系,既能满足精度要求,又能实现全线统一的坐标系以方便施工,减少不必要的成本,是有重大意义的。
1 基于高程补偿法建立平面坐标系高铁线路一般会通过高山峻岭地区,不可避免地会存在大坡度线路,即线路中各处大地高存在较大差异,在不考虑其他变形的情况下,在满足长度变形不大于10 mm/km的前提下[2, 9],一个投影带在高程方向最多只能控制高差不大于128 m,而在实际高铁线路中,高铁线路高差显然远远大于128 m。这样,在应用高斯投影和兰勃特投影模型建立高铁独立坐标系时必然会产生多个坐标系。针对这两种投影模型的不足,结合高速铁路线路的特点,即高铁线路呈直线延伸,左右摆动不大,在不考虑高程归化引起长度变形的前提下,大部分高铁线路采用双重投影方式,只需建立一个投影带便可控制投影面至平面的长度变形不大于10 mm/km。而此时影响投影长度变形的主要因素便是高程归化的影响,这里结合高铁建立控制网的特点,即全线采用GPS方式建立CPI控制网及部分CPII控制网,本文提出一种高程补偿法建立全线统一坐标系。
高程补偿法建立坐标系的基本思想是:根据线路走向以及控制点坐标,确定双重投影中线以及投影面大地高,先进行双重投影,得到各控制点相应的平面坐标,依次计算每条边归算到投影面的长度变形值,然后依据起算点坐标值以及各条边的反算值,在不改变每条边方向的前提下改正每条边的长度,并重新解算各控制点的平面坐标。
按照文献[2]的相关要求解算得到控制点在国家参考椭球下的大地坐标(B, L, H), 确定双重投影的投影面大地高Hm,这里取测区平均大地高为投影面大地高:
| $ {H_m} = \frac 1 n\sum\limits_{i = 1}^n {{H_i}} $ | (1) |
式中,Hi为各控制点大地高。
根据投影面大地高Hm构造工程椭球,由控制点的大地坐标(B, L)可确定双重投影的投影中线,再由双重投影建立平面坐标的方式得到各控制点的平面坐标(x, y, H, )由平面坐标便可计算得到各条边的边长值Si和高程归化改正值ΔSi:
| $ \left\{ \begin{array}{l} {S_i} = \sqrt {{{\left( {{x_{i + 1}} - {x_i}} \right)}^2} + {{\left( {{y_{i + 1}} - {y_i}} \right)}^2}} \\ \Delta {S_i} = \frac{{\left( {{H_{i + 1}} + {H_i}} \right){S_i}}}{{2R}} \end{array} \right. $ | (2) |
以线路起始点(x0,y0)为起算点,结合式(2) 便可计算各控制点新的平面坐标(x′,y′):
| $ \left\{ \begin{array}{l} {{x'}_0} = {x_0},{{y'}_0} = {y_0}\\ {x'_{i + 1}} = {x_i} + \left( {{S_i} + \Delta {S_i}} \right)\cos \left( {\left( {{x_{i + 1}} - {x_i}} \right)/{S_i}} \right)\\ {y'_{i + 1}} = {y_i} + \left( {{S_i} + \Delta {S_i}} \right)\cos \left( {\left( {{y_{i + 1}} - {y_i}} \right)/{S_i}} \right) \end{array} \right. $ | (3) |
式中,i=0, 1, 2, …, n。
式(3) 即为各控制点基于高程补偿建立的平面坐标系的坐标值的计算式。需要注意的是,式(3) 计算坐标值时保证了各边的方向值保持不变,即这种方式建立的平面坐标系保证了实地上的相对关系,方便线路设计人员进行坐标设计。
高程补偿建立平面坐标系的流程图如图 1所示。
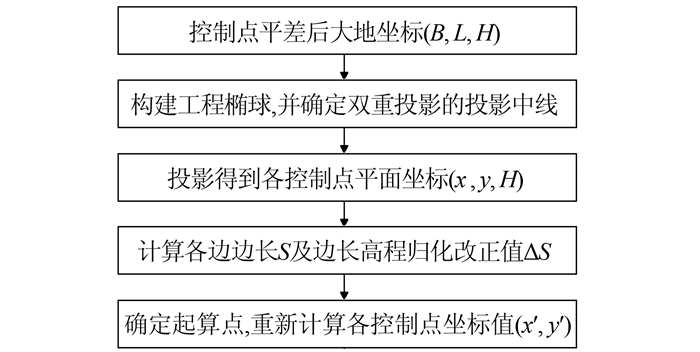 |
| 图 1 高程补偿法建立坐标系的流程 Figure 1 Flow Chart of Establishing Coordinate System Based on Elevation Compensation |
2 实例分析 2.1 工程概况
兰新高速铁路自兰州西站引出,横跨新疆、甘肃、青海三省区,线路为Ⅰ级双线,设计时速为350 km/h。
本文对兰新线中的嘉峪关至甘肃省省界柳园测段进行分析,路线长约330 km。该测区位于东经94°58′~98°05′;北纬39°48′~41°21′。线路呈西南-东北走向,该测段共布设有CPII点314个,CPI点92个;该段线路设计坡度大(最大坡度达20‰),线路高程变化剧烈,如图 2所示。
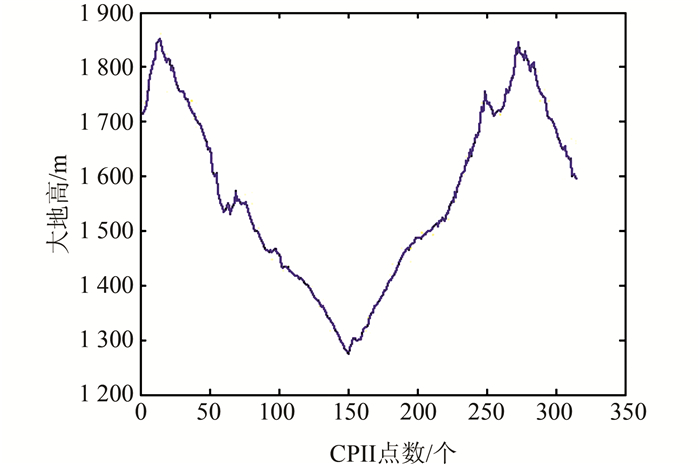 |
| 图 2 沿线CPII点大地高 Figure 2 Geodetic Height of CPII |
2.2 基于高程补偿法建立的坐标系
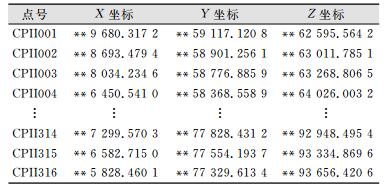
该控制网按照文献[2]的要求进行平差计算,并得到CPII点基于CGCS2000椭球的空间直角坐标(X,Y,Z)以及大地坐标(B,L,H),其中部分CPII点坐标如表 1所示,为了保证数据的保密性,各坐标的前两位均用“*”号表示。
| 表 1 CPII空间直角坐标/m Table 1 CPII Spatial Rectangular Coordinate/m |
 |
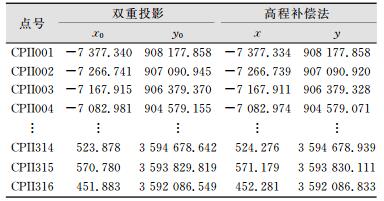
利用高程补偿法建立坐标系的方法进行计算。根据测区情况,取测区平均大地高1 567 m为投影面高程,测区中心纬度为40°20′00″,按照最小二乘方法确立投影中线,进行双重投影,得到各控制点的平面坐标;然后根据各点大地高计算各边边长改正,进而计算各控制点新的坐标,从而实现双重投影及高程补偿法建立的平面坐标,将两种方法建立的控制点坐标进行对比分析,其结果如表 2所示。
| 表 2 各控制点对应坐标/m Table 2 Corresponding Coordinates of Control Points/m |
 |
由表 2所列的坐标值可分别计算各条边的方位角以及相邻边的夹角,得出的结果均一致,只是改变了各条边的长度。高程补偿法建立的平面坐标系在各点产生的长度变形如图 3所示。由图 3可知,长度变形远远小于10 mm/km的要求。
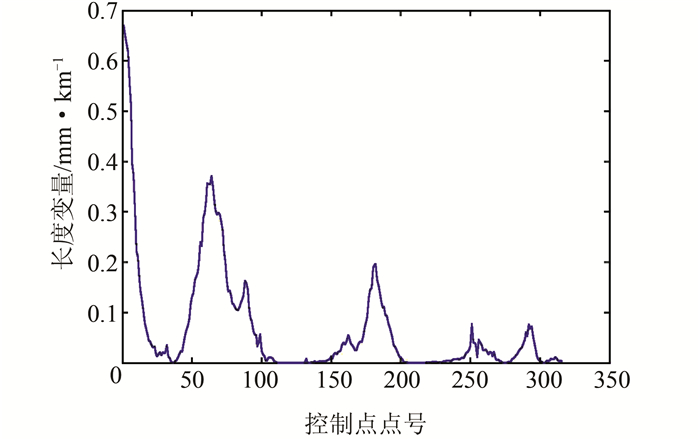 |
| 图 3 控制点投影变形情况 Figure 3 Change of Control Points Projection |
为进一步说明由平面坐标反算的两点距离与实地测量的距离的差值,下面分别将双重投影和高程补偿法得到的坐标反算出来的距离与实地理论距离进行比较,表 3给出了部分边长值的比较,图 4则表示了沿线边长长度变形值。这里的实地理论测量距离是由2000国家参考系下的空间直角坐标(X,Y,Z)以及各点对应的大地高H进行解算的。由表 3和图 4可知,高程补偿法建立的平面坐标系很好地解决了长度变形的问题,并且全线真正实现了平面坐标系统一的目的。
| 表 3 相邻控制点边长长度值 Table 3 Length of Adjacent Control Points |
 |
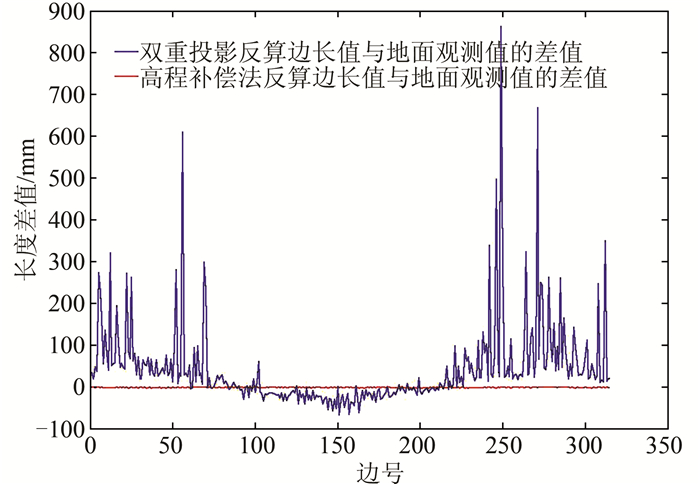 |
| 图 4 坐标反算边长与实测边长的差值 Figure 4 Difference of the Length Calculated by Coordinates and Measured Length |
3 结束语
本文提出了高程补偿法建立平面坐标系的方法,在不改变每条边方向的前提下,改正每条边的长度并重新解算各控制点的平面坐标。结合工程实例,对比分析了各种建立平面坐标系的方法,并得到由坐标反算边长和实测边长的差值。由此可知,本文方法很好地解决了长度变形的问题,并且真正实现了全线统一平面坐标系的目的,为高铁的施工提供了便利。
| [1] |
中华人民共和国铁道部. 高速铁路测量规范: TB10601-2009[S]. 北京: 中国铁道出版社, 2009 |
| [2] | 铁道第二勘察设计院. 客运专线无碴轨道铁路工程测量暂行规定[M]. 北京: 中国铁道出版社, 2006 |
| [3] | 刘中华. 荷比高速铁路Rheda2000无碴轨道测量技术[J]. 山西建筑, 2007, 33(18): 347–348 DOI: 10.3969/j.issn.1009-6825.2007.18.218 |
| [4] | 梁永. 高速铁路测量建立独立坐标系的数学模型[J]. 铁道工程学报, 2006, 23(7): 34–36 |
| [5] | 孙金礼. 基于矿区GPS网投影带和投影面的合理选择[J]. 辽宁工程技术大学学报, 2008, 27(5): 665–667 |
| [6] | 赵建三, 封良泉, 陈宗成. 具有抵偿面的任意带高斯投影法的应用[J]. 工程勘察, 2009, 37(7): 59–62 |
| [7] | 王怀念, 邱胜强, 王良民, 马瑞华. 济源市独立坐标与国家坐标的转换[J]. 测绘信息与工程, 2007, 32(5): 32–35 |
| [8] | 王璇, 姚连璧. 兰勃特投影在高速铁路测量中的应用[J]. 铁道勘察, 2014, (6): 17–20 |
| [9] | 武江伟, 高红光, 朴盛莲, 等. 长距离供水工程测量平面坐标系的选择[J]. 测绘地理信息, 2015, 40(3): 74–76 |
 2017, Vol. 42
2017, Vol. 42

