| 一种组合EEMD与PCA的GPS台站噪声消除方法 |
影响GPS定位精度的因素主要有大气延迟和多路径效应、卫星和接收机钟误差、轨道误差和观测噪声等[1],其中卫星和接收机钟误差通常采用差分定位技术来消除或削弱其影响,而多路径误差由于具有较强的周日重复性,通常利用改进的恒星日滤波方法来消除[2, 3]。相较于差分定位技术,精密单点定位(precise point positioning,PPP)采用非差观测模型,无需高密度的基站支持,其缺点是基于实数解的PPP不仅需要更长的观测时间,其精度与可靠性也比较低[4]。PRIDE PPP-AR是一款GPS数据后处理软件,可获得GPS数据非差模糊度的整数固定解,有效提高PPP中的收敛速度和定位精度,但所得坐标残差时间序列中仍存在一定的不规则变化和观测噪声。目前,消除噪声的方法主要有小波分析和集合经验模态分解(ensemble empirical mode decomposition,EEMD),后者的优势在于无需基函数,因此具有更好的自适应性[5]。此外,一些学者发现,在GPS坐标时间序列中还存在某种与时空相关的噪声,这种区域相关的误差被称为共模误差[6-8]。传统的时空滤波方法主要是堆栈滤波法,但不同站点间具有不同的共性误差分布,因此堆栈滤波法的应用受到了一定的限制[9]。而利用主成分分析(principal component analysis,PCA)可以有效剔除序列中的共模误差[10, 11]。本文将联合EEMD与PCA方法,对利用PPP-AR软件解算的GPS坐标时间序列进行空间滤波处理,以削弱或去除序列中的噪声及共模误差,提高站点坐标定位精度。
1 算法及流程 1.1 EEMD由于经验模态分解(empirical mode decomposition,EMD)中存在模态混叠问题,Wu等[12]对EMD方法进行了改进,提出了EEMD方法,在原始信号中加入n次幅值标准差为α(α取值范围通常为0.01~0.5[13])的高斯白噪声,对第i次加入高斯白噪声后的信号利用EMD方法进行分解,可有效抑制模态混叠现象。计算n次分解得到的本征模态函数(intrinsic mode function,IMF)分量的总体平均,并将其作为最终结果,通过剔除高频IMF分量消除噪声。
1.2 PCA假设对某区域内的n个连续运行基准站(continuously operating reference station,CORS)系统站点同步观测了m个历元,得到各站点的坐标时间序列xi (tj),去均值处理后,将结果排列成一个m×n的矩阵X,求取X的协方差阵,记为CX,再对CX进行特征值分解,得到:
| $ \boldsymbol{C_{X}}=\boldsymbol{V D V}^{\mathrm{T}} $ | (1) |
式中,V为特征向量矩阵,转置后各行向量对应各主成分的空间响应;D为对角阵,斜对角元素为特征值。计算各主成分贡献率
| $ \boldsymbol{D}=\operatorname{diag}\left(a_{1}, a_{2}, \cdots, a_{n}\right) $ | (2) |
利用EEMD方法虽然可以去除或削弱GPS坐标序列中的观测噪声、大气延迟误差等,但无法提取出序列中存在的共模误差,而利用PCA可以很好地分离序列中的共模误差。基于此,本文提出一种组合EEMD及PCA的方法,以消除GPS台站噪声的影响。首先,对原始GPS台站观测数据进行预处理,得到GPS坐标残差时间序列;然后,利用EEMD对序列进行分解,选择合适的高频分量作为随机噪声予以剔除,重构剩余IMF分量与残余分量;最后,对重构序列进行PCA处理,分离并消除序列中的共模误差。
2 实际数据处理与分析 2.1 数据预处理本文以中国香港GPS CORS系统站网为实验网,选取其中9个站点组成区域网,将其2015年4月23日,采样间隔为5 s的观测数据作为处理数据,首先利用PRIDE PPP-AR软件处理原始GPS数据,得到各站点1984世界大地测量系统(world geodetic system 1984,WGS-84)坐标三分量(X,Y,Z)时间序列,再通过坐标转换、去均值处理得到各站点(N,E,U)坐标残差序列。
2.2 EEMD去噪将残差序列作为EEMD的输入信号x(t),在x(t)中分100次加入均值为0、信噪比为0.2的高斯白噪声,并利用EMD方法进行分解。本文以HKSC站N方向为例进行说明,分解得到14个IMF分量和1个残余分量,对各IMF分量进行分析,可认为前6个IMF分量为高频的随机噪声,予以剔除,重构剩余的8个IMF分量与残余分量,得到去噪后的坐标残差序列,结果见图 1。
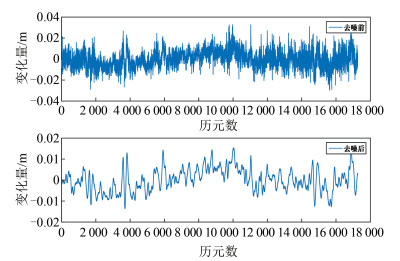 |
| 图 1 EEMD去噪前后HKSC站N方向的残差序列 Fig.1 Residual Series in the N Direction of HKSC Station Before and After Being Denoised by EEMD |
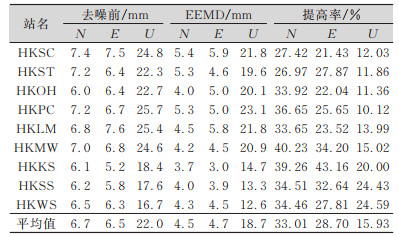
计算各站点经EEMD去噪后的坐标时间序列三分量(N,E,U)与原始坐标时间序列的标准差,如表 1所示。结果表明,原始坐标时间序列经EEMD处理后,精度明显提高,各站点坐标三分量精度的平均提高值分别为33.01%、28.70%、15.93%。
| 表 1 EEMD去噪前后序列标准差 Tab.1 Standard Deviations of Series Before and After Being Denoised by EEMD |
 |
2.3 PCA空间滤波
通过PCA空间滤波方法对所得残差坐标时间序列进行主成分分析,得到前3个主成分(PC1,PC2,PC3)的空间响应,如图 2所示。可以看出,各站点PC1在3个坐标分量上的空间响应值变化平稳,具有一致的空间响应,PC2和PC3空间响应变化较大。
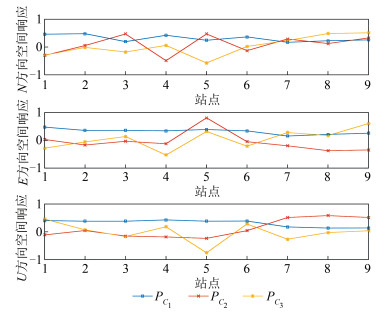 |
| 图 2 PC1~PC3对应的空间响应 Fig.2 Spatial Responses of PC1~PC3 |
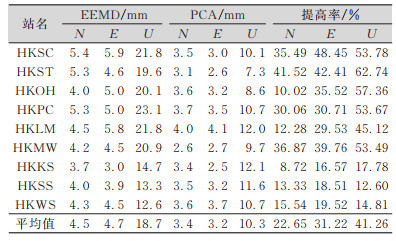
计算各主成分在3个坐标分量上的贡献率,可得:PC1在3个坐标分量上的贡献率分别为42.45%、54.82%、70.06%;PC2在3个坐标分量上的贡献率分别为13.00%、10.28%、8.79%;PC3在3个坐标分量上的贡献率分别为11.52%、9.84%、5.41%。综合PC1空间响应的一致性和对坐标序列的贡献率,可将其作为区域网的共模误差予以剔除。计算PCA空间滤波前后坐标时间序列的标准差,结果见表 2,可以发现,序列经PCA滤波后,精度进一步提高,9个站点坐标三分量时间序列的平均中误差分别为3.4 mm、3.2 mm、10.3 mm,各站坐标三分量精度的平均提高值分别为22.65%、31.22%、41.26%,说明通过PCA空间滤波方法可以较好地分离监测站间的共模误差。
| 表 2 PCA滤波前后序列标准差对比 Tab.2 Comparison of Series Standard Deviations After PCA Filtering |
 |
3 结束语
本文基于PPP-AR模糊度快速重收敛技术,利用PRIDE PPP-AR软件处理GPS台站观测数据,对中国香港CORS系统站点坐标时间序列进行实验,分析发现,通过EEMD方法能有效削弱GPS台站接收机的观测噪声,结合PCA空间滤波,可以有效地分离出GPS台站坐标时间序列中的共模误差,提高了GPS单点定位精度。
| [1] |
戴吾蛟. GPS精密动态变形监测的数据处理理论与方法研究[D]. 长沙: 中南大学, 2007
|
| [2] |
张成龙, 刘超, 赵兴旺, 等. 基于改进EEMD的GPS多路径误差建模与削弱方法研究[J]. 大地测量与地球动力学, 2018, 38(10): 1 021-1 026. |
| [3] |
Choi K, Bilich A, Larson K M, et al. Modified Sidereal Filtering: Implications for High-Rate GPS Positioning[J]. Geophysical Research Letters, 2004, 31(22): L22608. |
| [4] |
张小红, 李星星. 非差模糊度整数固定解PPP新方法及实验[J]. 武汉大学学报·信息科学版, 2010, 35(6): 657-660. |
| [5] |
罗飞雪, 戴吾蛟. 小波分解与EMD在变形监测应用中的比较[J]. 大地测量与地球动力学, 2010, 30(3): 137-141. |
| [6] |
田云锋, 沈正康. GPS坐标时间序列中非构造噪声的剔除方法研究进展[J]. 地震学报, 2009, 31(1): 68-81. DOI:10.3321/j.issn:0253-3782.2009.01.008 |
| [7] |
殷海涛, 甘卫军, 熊永良, 等. PCA空间滤波在高频GPS定位中的应用研究[J]. 武汉大学学报·信息科学版, 2011, 36(7): 825-829. |
| [8] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报·信息科学版, 2018, 43(12): 2 112-2 123. |
| [9] |
Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3): B03405. |
| [10] |
贺小星, 花向红, 周世健, 等. PCA与KLE相结合的区域GPS网坐标序列分析[J]. 测绘科学, 2014, 39(7): 113-117. |
| [11] |
吴丰波, 岳国森, 梁敬祖, 等. 基于PCA及提升小波组合算法提取建筑物结构振动信号[J]. 大地测量与地球动力学, 2016, 36(9): 808-812. |
| [12] |
Wu Z H, Huang N E. Ensemble Empirical Mode Decom position: A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [13] |
陈忠, 符和超. 基于EEMD方法的永磁同步电机电磁噪声诊断[J]. 振动与冲击, 2013, 32(20): 124-128. DOI:10.3969/j.issn.1000-3835.2013.20.024 |
 2022, Vol. 47
2022, Vol. 47

