| 加权优选方法在信号分解中的应用与软件研制 |
Huang等[1]提出利用EMD(empirical mode decomposition)模型的时频分析方法,确立了EMD模型的基本框架,强调EMD模型的基本依据,其完备性和正交性得到验证。经验模态分解EMD的实质是拆解包含多种特征频率的原始信号而得到多个平稳的子信号,即通过连续均值筛选和筛分准则将构成原始信号的具有不同特征频率的数据序列分解并提取,形成多个本征模态函数(intrinsic mode function, IMF)分量。影响EMD分解精度的因素主要有包络拟合函数、端点延拓方法、IMF筛分准则。针对包络拟合,Huang等[1]使用的是三次样条函数;Chen等[2]应用非均匀三次B样条函数;戴豪民等[3]尝试张力格林样条曲线。针对端点延拓,Zhao等[4]提出镜像延拓方法;黄大吉等[5]提出极值延拓法;刘慧婷等[6]利用极大/小值进行多项式拟合,进而得到端点处的极值信息;黄诚惕[7]提出边界局部特征尺度延拓法。针对筛分准则,标准差系数法[8](standard deviation, SD准则)是最早提出的判断方法;Rilling等[9]提出的准则(简称GR准则)具有更好的均值特征。李云飞[10]提出计算相关系数的绝对值(absolute value of correlation coefficent difference, AD准则)方法。
因此,如何从众多备选项中自动甄选出最适合目标出力信号的方法集就显得极为重要,故而本文提出加权优选方法。
1 经验模态分解经验模态分解的实质就是通过迭代将原始信号分解成多个平稳的子信号(即本征模态函数)和一个残余信号。
1.1 EMD分解流程1) 找出信号x(t)的局部极大值和局部极小值;
2) 使用合适的包络拟合函数分别对极大/小值点集进行包络拟合,同时进行离散点插值,进而得到离散的较大/小值(上/下)包络U(t)和D(t)。
3) 计算均值m(t),得到可能IMF值h(t),有:
| $ m(t) = \frac{{U(t) + D(t)}}{2} $ | (1) |
| $ h(t) = x(t) - m(t) $ | (2) |
4) 判断h(t)是否满足设定条件, 若满足则可将h(t)视为一个IMF分量;如果不满足则令x(t)=h(t)再次重复步骤1)~步骤3),直至h(t)满足设定条件。但是完全满足这两个设定条件极其困难,通常只要满足某种IMF筛分准则就可以将h(t)视为IMF分量。
迭代直至h(t)可视为IMF分量,则有IMF1=h(t),其中IMF1表示得到的第1个IMF,且下文中的IMFk表示得到的第k个IMF。
5) 计算余量r(t):
| $ r(t) = x(t) - {\rm{IM}}{{\rm{F}}_1} $ | (3) |
判断r(t)是否有必要进行下一次筛选,依据通常是余量信号的极大/小值的数目。如果需要,则令x(t)=r(t)来重复步骤1)~步骤4),直至r(t)无需再次筛选,最后的余量r(t)被视作残余信号,那么原始信息可以表示为:
| $ x(t) = \sum\limits_{k = 1}^n {{\rm{IM}}{{\rm{F}}_k} + {r_n}(t)} $ | (4) |
重构误差只有10-16量级,完全可以忽略。
影响EMD效果的有包络拟合、端点延拓和IMF筛分准则。
1.2 包络拟合函数1) 非扭结样条。该函数的本质是分段三次多项式,可以保证在内节点上,以及一/二阶导数上的连续性,而且无需知道一/二阶导数值。
2) 非均匀有理B样条。该函数的使用有正、反算之分。因为拟合数据是离散点集,所以仅用到反算,是在反算的基础上进行拟合,进而实现数据插值。
3) 格林样条曲线。该函数来源于弹性力学中弹性细杆的弯曲变形问题,那么样条曲线必然具有良好的光滑性。格林样条曲线有张力和无张力之分。无张力是细杆只受竖直力;张力是还受水平力。
同一信号的不同包络拟合效果如图 1所示。因为本文使用的是模拟数据,并无实际含义,因此文中图 1~图 6的横坐标仅表示数值,并无实际意义。
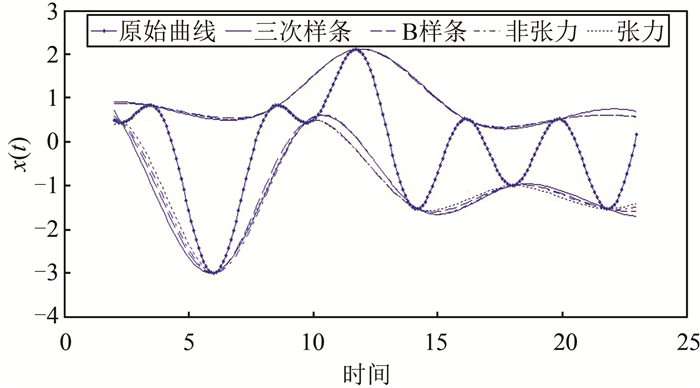 |
| 图 1 同一信号的不同包络拟合效果对比 Fig.1 The Comparison Between Different Envelope Fitting Methods Based on Same Signal |
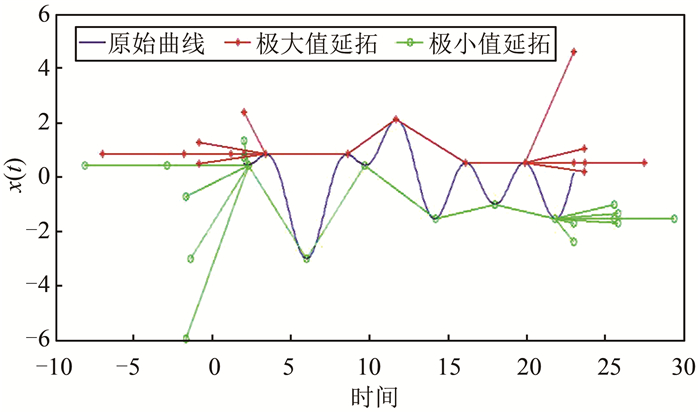 |
| 图 2 信号的不同延拓方法的比较 Fig.2 The Comparison Between Different Extension Method Based on Same Signal |
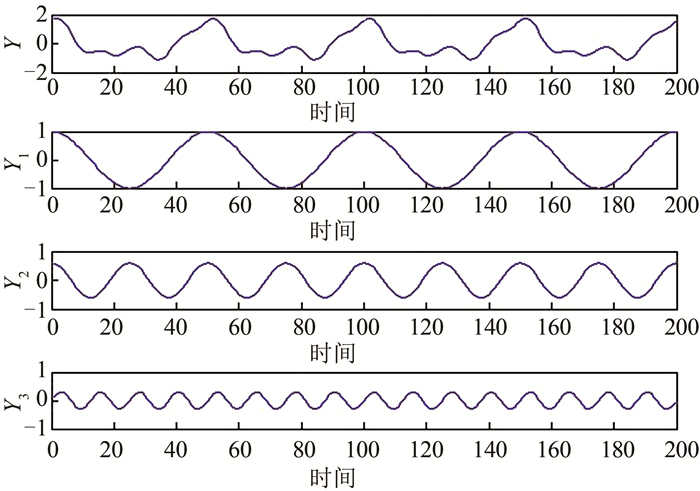 |
| 图 3 模拟信号的波形曲线 Fig.3 The Wavy Curve of Analog Signal |
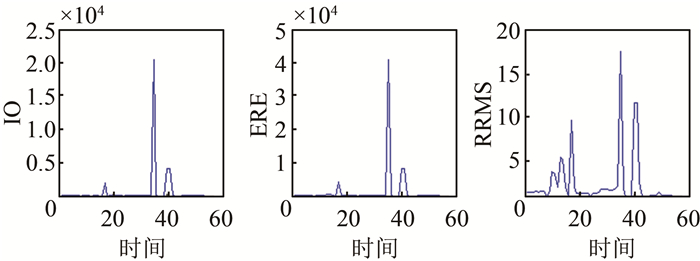 |
| 图 4 指标值过大的情况 Fig.4 The Condition of Oversized Values |
 |
| 图 5 331方法的分解结果及其残差值 Fig.5 The Decomposition Result and Its Residual Value Based on 331 Method |
 |
| 图 6 111方法的分解结果及其残差值 Fig.6 The Decomposition Result and Its Residual Value Based on 111 Method |
1.3 端点延拖方法
1) 端点镜像方法。该方法的实质是利用平面镜像原理将非周期性信号构造成周期性信号,周期长度与镜面的放置位置有关,通常是将平面镜放置在端点附件的极值点处;周期数取决于数据处理的复杂程度,通常取周期数为3即可。
2) 极值延拓法。该方法只涉及极值信息,与信号的其他信息无关,但是拟合出的极值点可能在定义域外,那么就要进行拟合并且插值完成后再取规定定义域内的数据点参与EMD剩余运算。
3) 多项式拟合法。设有N个极大或极小值点,则其必然可以用多项式进行拟合[11],至少要有4个数据点才能保证参数的唯一性。
4) 线性延拓法。作为最简单的延拓方法,线性延拓法所使用的点信息最少,具有最易计算机实现的优势。
5) 自回归延拓法。张郁山等[12]尝试利用极值信息建立自回归(auto-regressive, AR)模型进行端点处极值信息的预测。AR模型的本质是多元线性方程,可以看作是线性延拓法的升级版。鉴于随着迭代的进行,极值点的数量将逐渐减少,以防止上述现象导致的建模失败。因此需建立常用的二阶AR模型,即AR(2)模型[13]。
6) 边界特征延拓法。该方法的核心思想也是通过临近边界的几个极大/小值信息推算出边界上的极大/小值信息,但是与上述方法不同的是,该方法并不是基于这几个极值点信息拟合和插值,而是简单利用极值的横/纵坐标值。
以上6种端点延拓方法对同一模拟信号的延拓结果如图 2所示。
1.4 IMF筛分准则不同的IMF筛分准则影响IMF分量的个数和振幅,甚至影响分解结果的有效性。常用的包括SD准则、GR准则、AD准则[10]。最初的筛分依据是标准差系数,即SD准则,定义如下:
| $ {\rm{SD}} = \sum\limits_{t = 0}^T {\frac{{{{\left| {{h_{k + 1}}(t) - {h_k}(t)} \right|}^2}}}{{h_k^2(t)}}} $ | (5) |
式中,T是信号长度;ε是符合阈值,取值通常在0.2~0.3间。
GR准则为:
| $ \sigma (t) = \frac{{\left| {U(t) + D(t)} \right|}}{{\left| {U(t) - D(t)} \right|}} $ | (6) |
式中,U(t)、D(t)分别是极大与极小值的拟合包络线。
如果σ(t)中小于0.05的数目占总数的95%以上或所有σ(t)小于0.5;则认为可将hk(t)视为本征模态函数。
李云飞[10]利用信号相关系数差的绝对值进行判断,称为AD准则。当AD小于0.01时,即可认为该h(t)是本征模态函数:
| $ {\rm{AD}} = \left| {{\rho _{k, k}} - {\rho _{k - 1, k - 1}}} \right| $ | (7) |
式中,ρk, k是hk(t)和mk(t)间的相关系数。
2 加权优选方法经验模态分解的效果与包络拟合函数、端点延拓方法、IMF筛分准则的选择有关,但是并不是简单的正相关关系,也就是说相同方法无法保证对任意处理目标都能得到较优的IMF分量,故而本文提出一种以评价指标值为基础与依据的能够自动甄选的加权组合优选方法。
2.1 评价指标常用的评价指标包括能量相对误差(energy relative error, ERE)、相对均方根(relative root mean square, RRMS)、正交指数(index of orthogonality, IO)。
假设有原始信号x(t),采样值N,分解成n个IMF分量IMFi和一个残余分量rn(t),则有:
| $ {\rm{IO}} = \left| {\sum\limits_{t = 1}^N {\sum\limits_{i, j = 1}^n {{\rm{IM}}{{\rm{F}}_i}(t){\rm{IM}}{{\rm{F}}_j}(t)} } } \right|/\sum\limits_{t = 1}^N {{x^2}(t)} , i \ne j $ | (8) |
| $ {\rm{ERE}} = \left| {\sum\limits_{t = 1}^N {{x^2}(t)} - \sum\limits_{t = 1}^N {\sum\limits_{i = 1}^n {{\rm{IMF}}_i^2(t)} } } \right|/\sum\limits_{t = 1}^N {{x^2}(t)} $ | (9) |
| $ {\rm{RRMS}} = \left| {\sqrt {\sum\limits_{i = 1}^n {{\rm{RM}}{{\rm{S}}_{{\rm{IM}}{{\rm{F}}_i}}}} } - {\rm{RM}}{{\rm{S}}_{x(t)}}} \right|/{\rm{RM}}{{\rm{S}}_{x(t)}} $ | (10) |
| $ {\rm{RM}}{{\rm{S}}_{x(t)}} = \sqrt {\sum\limits_{i = 1}^n {{x^2}(t)/N} } $ | (11) |
| $ {\rm{RM}}{{\rm{S}}_{{{\rm{IMF}}_i}}} = \sqrt {\sum\limits_{i = 1}^n {{\rm{IMF}}_i^2(t)/N} } $ | (12) |
IO的值越小,说明各IMF分量之间的正交性越好;ERE的值越小,说明原始信号的能量损耗越低;同样的,RRMS的值也是越小越好。
2.2 加权优选方法EMD分解中,共计有3种包络拟合函数,6种端点延拓方法,3种IMF筛分准则,共计有54种选择,最原始的是三次样条曲线、SD准则的组合。除去少量结果异常项之外,绝大多数选择组合都能得到对应的分解结果。加权优选方法的提出是为了从这54种选择组合中甄选出针对处理目标而言最合适的方法。与经验选择方法相比,能够有效提升分解的效果。
假设有指标项Index_A、Index_B,以及对应的取值Ai、Bi,其中Index_A的取值是越大越好,Index_B的取值是越小越好,结果如表 1所示。
| 表 1 加权优选方法 Tab.1 Weighted Optimization Method |
 |
首先找出每个指标项的最优值,假设Index_A项的最优值是最大值,即maxA;Index_B项的最优值是最小值,即minB,然后将所有指标项的取值进行规范化,结果如表 2所示。
| 表 2 规范化结果 Tab.2 The Standardized Results |
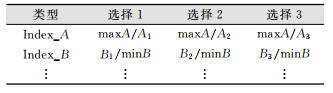 |
显然规范化后对应值都是不小于1的,而且原始取值越优异,规范化后的值是越接近1的。然后将所有指标项的规范化后的结果按照等加权原则直接相加得到整体规范值。显然这个整体规范值不小于指标项个数的值。
如果整体规范值越小(趋近3),那么认为该组选择组合在对比中的表现更好,分解效果最优。
3 模拟信号实验与软件研制本节利用仿真信号进行模拟试验,作对比的对象是用三次样条曲线、镜像延拓、SD准则的传统EMD分解,以便判断是否能够选择较优的方法。
模拟信号是由不同周期和振幅的函数构成,如式(13),波形趋势如图 3所示。
| $ \begin{array}{*{20}{c}} {Y(x) = \cos (\frac{{\rm{ \mathsf{ π} }}}{{25}}x) + \frac{3}{5}\cos (\frac{{2{\rm{ \mathsf{ π} }}}}{{25}}x) + \frac{3}{{10}}\cos (\frac{{4{\rm{ \mathsf{ π} }}}}{{25}}x) = }\\ {{Y_1} + {Y_2} + {Y_3}, x \in [1, 200]} \end{array} $ | (13) |
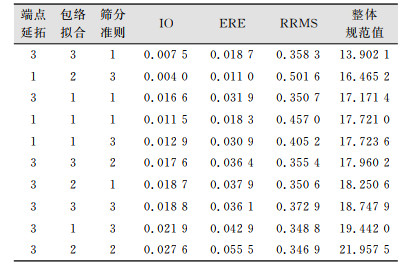
运行代码将得到54×6维(极少量的选择组合可能出现输出失败的情况)的结果信息。但是可能出现迭代发散以及指标值过大的可能性,即如图 4所示,最后共计有32组有效数据,再用加权组合方法计算出其整体规范值。篇幅有限,故而在此只列出最优的10组数据,如表 3所示。
从表 3可以看出,针对目标信号,本文所提方法认为最优的是非张力格林样条、极值延拓、SD准则,此时的整体规范值最小,故而将这种选择组合(331)与传统EMD方法(111)进行比较。结果与精度分别如图 5、图 6所示,图中V1、V2、V3为各IMF分量与原始信号的残差值。
| 表 3 十组最优的选择方法 Tab.3 The Ten Groups of Optimal Selection Method |
 |
两种方法的指标信息,包括每个IMF的方差、正交指数IO值等,如表 4所示。
| 表 4 EMD实验结果统计 Tab.4 The Statistical Result of EMD Experiment |
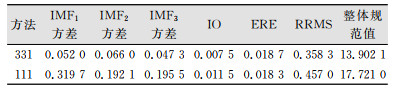 |
结合表 4和图 5、图 6可以看出,加权组合优选方法的结果明显优于传统EMD方法的分解结果,而且传统EMD分解得到4个本征模态函数,但是构造曲线只包含3个部分。可以说,优选方法不仅在还原精度上高于传统EMD,在还原准确性上也是高于传统EMD的。
Matlab软件[14]的数据计算功能强大,而且自带可视化界面GUI工具,能够满足界面化、模块化[15]等功能需求。加权优选方法算法设计如图 7所示,图中,i表示第i种包络拟合曲线;j表示第j种端点延拓方法;k表示第k种IMF筛分准则。
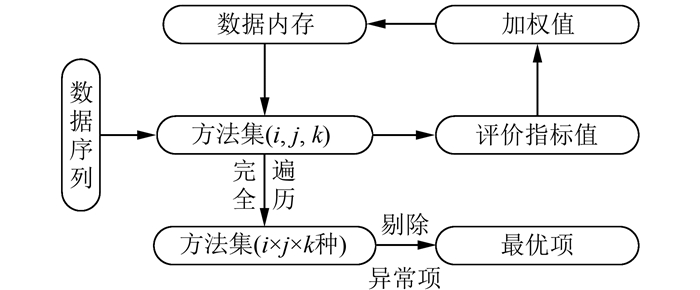 |
| 图 7 算法设计 Fig.7 Design of the Algorithm |
4 结束语
加权优选方法的实质就是先行对所有方法集实现完全遍历,然后计算出对应的结果与信息,然后基于IO、ERE、RRMS算出的整体规范值,判断出最合适的方法组合。模拟信号实验证明了该方法在精度与准确性上的优势,加权组合择优方法在提高EMD分解的效果方面完全是可行的。另外,利用EMD方法消除GPS信号中的多路径效应已得到证明,因此该方法及软件是对GPS信号处理与挖掘方法的重要补充。
| [1] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Royal Society, 1998, 454(1 971): 903-995. |
| [2] |
Chen Q H, Huang N, Riemenschneider S, et al. A B-Spline Approach for Empirical Mode Decompositions[J]. Advances in Computational Mathematics, 2006, 24(1/4): 171-195. |
| [3] |
戴豪民, 许爱强. 基于张力格林样条的EMD均值曲线插值方法[J]. 计算机工程与设计, 2015, 36(2): 401-405. |
| [4] |
Zhao J P, Huang D J. Mirror Extending and Circular Spline Function for Empirical Mode Decomposition Method[J]. Journal of Zhejiang University:Science A, 2001, 2(3): 247-252. DOI:10.1631/jzus.2001.0247 |
| [5] |
黄大吉, 赵进平, 苏纪兰. 希尔伯特-黄变换的端点延拓[J]. 海洋学报(中文版), 2003(1): 1-11. |
| [6] |
刘慧婷, 张旻, 程家兴. 基于多项式拟合算法的EMD端点问题的处理[J]. 计算机工程与应用, 2004(16): 84-86. |
| [7] |
黄诚惕.希尔伯特-黄变换及其应用研究[D].成都: 西南交通大学, 2006 http://cdmd.cnki.com.cn/Article/CDMD-10613-2006091556.htm
|
| [8] |
徐斌, 徐德城, 朱卫平, 等. 希尔伯特-黄变换方法的改进[J]. 西北工业大学学报, 2011, 29(2): 268-272. |
| [9] |
Rilling G, Flandrin P, Goncalves P. On Empirical Mode Decomposition and Its Algorithms[C]. IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing, Grado, Italy 2003
|
| [10] |
李云飞.基于改进的HHT方法提取重力固体潮信号的地球物理信息[D].昆明: 昆明理工大学, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10674-1015641488.htm
|
| [11] |
王中华, 花向红, 杨克明, 等. 大型基坑工程水平位移监测与预测结果分析[J]. 测绘地理信息, 2014, 39(5): 50-53. |
| [12] |
张郁山, 梁建文, 胡聿贤. 应用自回归模型处理EMD方法中的边界问题[J]. 自然科学进展, 2003(10): 48-53. |
| [13] |
高昂, 许运鹏, 李新社, 等. 半参数AR模型在隧道拱顶沉降分析中的应用[J]. 测绘地理信息, 2018, 43(1): 70-72. |
| [14] |
舒颖, 花向红, 贺小星, 等. GPS时间序列数据处理与分析软件的设计及实现[J]. 测绘地理信息, 2017, 42(5): 29-32. |
| [15] |
李宏博, 史先琦, 李永旭. 测绘项目信息管理软件系统研制[J]. 测绘地理信息, 2015, 40(5): 49-51. |
 2020, Vol. 45
2020, Vol. 45

