| 傅里叶级数修正的动态GM (1, 1) 模型在沉降预测中的应用 |
2. 武汉大学灾害监测和防治研究中心,湖北 武汉,430079
2. Hazard Monitoring & Prevention Research Center, Wuhan University, Wuhan 430079, China
高速铁路以其运输力强、速度快、能耗低、安全性好等特点已经成为我国客运发展的趋势。高速铁路两个重要的特点是高平顺性和高稳定性,这两个特点决定了线下工程沉降变形监测的意义和重要性[1],所以对高速铁路线下工程的沉降分析与预测成为一个重点研究问题。
灰色GM (1, 1) 模型计算简便,不需要大量的原始时间序列数据即可获得较好的预测结果,已广泛应用于变形监测中[2]。实时地引入了新观测值的动态GM (1, 1) 模型真实反映了系统状态的变化,可以有效地提高预测精度[3]。但是这些模型没有对残差进行建模就用于预测值修正,本文将观测值看作由趋势项和残差项两部分构成,应用动态GM (1, 1) 模型对趋势项进行预测,然后利用傅里叶级数对残差部分进行拟合,得出用于修正预测值的残差,将此修正方法用于动态GM (1, 1) 模型,得出傅里叶级数修正的动态GM (1, 1) 模型,最后通过对比分析,证明了傅里叶级数修正的动态GM (1, 1) 模型有更高的预测精度。
1 傅里叶级数修正的动态GM (1, 1) 模型 1.1 动态GM (1, 1) 模型设原始观测序列为[4]:
| $ {\boldsymbol{X}^{(0)}}=({{x}^{(0)}}(1), {{x}^{(0)}}(2), \cdots, {{x}^{(0)}}(n)), n\ge 4 $ | (1) |
式中,X(0)是一个非负序列;n为序列的长度。当对X(0)进行一次累加生成 (1-AGO) 时,就可以得到序列X(1),很明显X(1)是单调增加的。
| ${{\mathit{\boldsymbol{X}}}^{(1)}}=({{x}^{(1)}}(1), {{x}^{(1)}}(2), \cdots, {{x}^{(1)}}(n)), n\ge 4$ | (2) |
| $ {{x}^{(1)}}(k)=\sum\limits_{i=1}^{k}{{{x}^{(0)}}(i), k=1, 2, \cdots, n} $ | (3) |
可以定义如下的生成均值序列:
| ${{\mathit{\boldsymbol{Z}}}^{(1)}}=({{z}^{(1)}}(2), {{z}^{(1)}}(3), \cdots, {{z}^{(1)}}(n))$ | (4) |
式中,z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1), k=2, 3, …, n。
对X(1)建立一阶微分方程:
| $\frac{d{{\mathit{\boldsymbol{X}}}^{(1)}}}{dt}+a{{\mathit{\boldsymbol{X}}}^{(1)}}=u$ | (5) |
式中,a和u为模型待估参数,可记为灰参数向量â=[a, u],它可以由式 (6) 求得:
| $\mathit{\boldsymbol{\hat a}} = {({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}})^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{Y}}_N}$ | (6) |
式中,
解出â代入式 (5),解出微分方程得:
| ${\hat x^{(1)}}(k + 1) = ({x^{(0)}}(1) - \frac{u}{a}){{\rm{e}}^{ - ak}} + \frac{u}{a}$ | (7) |
对
| ${\hat x^{(0)}}(k + 1) = \left[{{x^{(0)}}(1)-\frac{u}{a}} \right]{{\rm{e}}^{ - ak}}(1 - {{\rm{e}}^a})$ | (8) |
当k < n时,称
在GM (1, 1) 模型中,只有两个参数,所以用很少的数据便可以建立模型进行预测,这是灰色预测模型的优点。但是高铁路基的沉降是一个动态变化的过程,在监测的前期,沉降速度快,后期变形趋于稳定,沉降速度变慢,所以两个固定参数不能有效地表示出模型状态的变化。要想反映出系统最新的状态,就要对模型进行动态处理,在进行过一次预测后,对原始观测序列进行更新,具体做法是在式 (1) 加入最新信息x(0)(n+1),去掉最旧信息x(0)(1),得到新的原始观测序列:
| ${\mathit{\boldsymbol{X}}^{(0)}} = ({x^{(0)}}(2), \cdots, {x^{(0)}}(n), {x^{(0)}}(n + 1)), n \ge 4$ | (9) |
用这种将数据更新得到观测序列的方法得到的GM (1, 1) 模型就是动态GM (1, 1) 模型。该模型原始观测序列的数据量始终保持在n个,n叫做该模型的等维约束条件。这样的模型稳定性强,且模型参数在整个过程中不断的被更新,反映出了系统最新的状态。因此,动态GM (1, 1) 模型的预测精度比传统的GM (1, 1) 模型有很大的提高[3]。
1.2 傅里叶级数修正模型定义X(0)的残差序列:
| ${\mathit{\boldsymbol{E}}^{(0)}} = ({e^{(0)}}(2), {e^{(0)}}(3), \cdots, {e^{(0)}}(n))$ | (10) |
式中,
在式 (10) 中的残差可展开为傅里叶级数,表示如下[5, 6]:
| $ {e^{(0)}}(k) = \frac{1}{2}{a_0} + \sum\limits_{i = 1}^z {\left[{{a_i}\cos (\frac{{2\pi i}}{T}k) + {b_i}\sin (\frac{{2\pi i}}{T}k)} \right], k = 2, 3, ..., n} $ | (11) |
其中,T=n-1;
式 (11) 可以被写成:
| ${\mathit{\boldsymbol{E}}^{(0)}} = \mathit{\boldsymbol{PC}}$ | (12) |
式中, P和C定义如下:
| $ \begin{array}{l} P = \left[{\begin{array}{*{20}{c}} {\frac{1}{2}}&{\cos (2\frac{{2\pi }}{T})}&{\sin (2\frac{{2\pi }}{T})}&{\cos (2\frac{{2\pi }}{T}2)}\\ {\frac{1}{2}}&{\cos (3\frac{{2\pi }}{T})}&{\sin (3\frac{{2\pi }}{T})}&{\cos (3\frac{{2\pi }}{T}2)}\\ \vdots & \vdots & \vdots & \vdots \\ {\frac{1}{2}}&{\cos (n\frac{{2\pi }}{T})}&{\sin (n\frac{{2\pi }}{T})}&{\cos (n\frac{{2\pi }}{T}2)} \end{array}} \right.\\ \left. {\begin{array}{*{20}{c}} {\sin (2\frac{{2\pi }}{T}2)}& \cdots &{\cos (2\frac{{2\pi }}{T}z)}&{\sin (2\frac{{2\pi }}{T}z)}\\ {\sin (3\frac{{2\pi }}{T}2)}& \cdots &{\cos (3\frac{{2\pi }}{T}z)}&{\sin (3\frac{{2\pi }}{T}z)}\\ \vdots & \vdots & \vdots & \vdots \\ {\sin (n\frac{{2\pi }}{T}2)}& \cdots &{\cos (n\frac{{2\pi }}{T}z)}&{\sin (n\frac{{2\pi }}{T}z)} \end{array}} \right] \end{array} $ | (13) |
| $ \mathit{\boldsymbol{C}} = {\left[{{a_0}, {a_1}, {b_1}, {a_2}, {b_2}, \cdots, {a_z}, {b_z}} \right]^{\rm{T}}} $ | (14) |
可以使用最小二乘原理对式 (12) 进行求解,得出:
| $\mathit{\boldsymbol{C}} = {\left[{{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right]^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{E}}^{(0)}}$ | (15) |
由傅里叶级数修正后的预测值如下:
| $ \hat x_f^{(0)}(k) = {\hat x^{(0)}}(k)-{\hat e^{(0)}}(k), k = 2, 3, \cdots, n + 1 $ | (16) |
GM (1, 1) 模型常用的精度评定办法为后验差检验,它是对残差分布的统计特性进行检验,设S1、S2分别为原始序列X(0)和残差序列E(0)的均方差,则后验差C=S2/S1越小,模型越好,而小误差
由于常用的后验差检验总是能满足1级指标,即后验差C≤0.35,小误差概率P≥0.95,所以本文中采用如下精度指标来表示模型精度[8]:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{{n-1}}\sum\limits_2^n {{{\left( {{e^{(0)}}(k)} \right)}^2}} } $ | (17) |
| $ {\rm{ARPE}} = \frac{1}{{n-1}}\sum\limits_2^n {\frac{{|e(k)|}}{{{x^{(0)}}(k)}}} $ | (18) |
其中,e、RMSE和ARPE分别表示残差、均方根误差和平均相对百分比误差。
2 工程实例应用分析为验证算法的可行性,证明利用傅里叶级数修正后的动态GM (1, 1) 模型在预测中有更好的效果,现以某高铁路基某监测点的42期沉降观测数据进行计算分析,原始观测数据如表 1所示。
| 表 1 某高铁路基某监测点的累计沉降量 Table 1 Cumulative Subsidence of a High-speed Rail Monitoring Point |
 |
将动态GM (1, 1) 模型和傅里叶级数修正的动态GM (1, 1) 模型的预测结果进行对比,比较的精度指标为中误差和平均相对百分比误差。本文采用动态模型的等维约束为10,即在式 (9) 中n=10。预测结果如表 2所示,原始观测值与两种模型的预测值曲线如图 1所示,其中GM (1, 1) 表示未修正的动态GM (1, 1) 模型,EFGM (1, 1) 表示傅里叶级数修正的动态GM (1, 1) 模型。
| 表 2 动态GM (1, 1) 模型与傅里叶级数修正的动态GM (1, 1) 模型预测结果对比 Table 2 Prediction Results Comparison Between GM (1, 1) Model and EFGM (1, 1) Model |
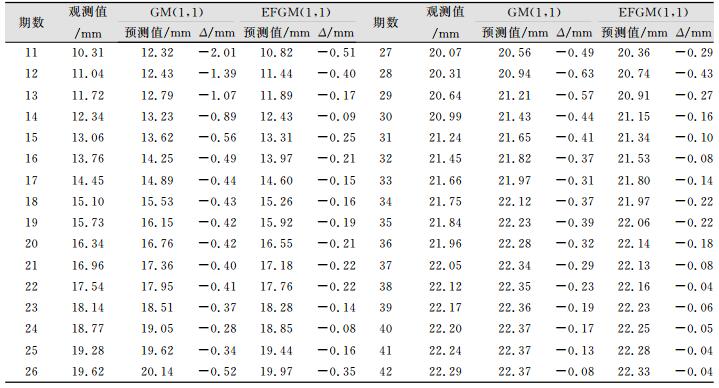 |
由表 2及图 1可以看出,这种动态GM (1, 1) 模型和傅里叶级数修正的动态GM (1, 1) 模型均有较好的预测结果,在每一个数据的预测上,傅里叶级数修正的动态GM (1, 1) 模型都优于动态GM (1, 1) 模型。在变形前期,由于沉降值的变化大,系统不太稳定,所以未修正的动态GM (1, 1) 模型预测结果精度不高,利用傅里叶级数修正的效果非常明显,特别是11、12、13、14期,这几期残差值降低到了原来的1/4;在变形后期,变形趋于稳定,两种模型预测值精度都很高,但是修正后的预测值残差都更小,修正也是有效的。
 |
| 图 1 两种模型的预测值比较以及残差比较 Figure 1 Prediction and Residual Comparison of Two Models |
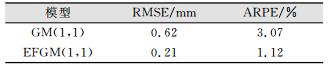
表 3给出了两种模型的总的精度指标的比较,普通的动态GM (1, 1) 模型的中误差为0.62 mm,修正之后中误差可以达到0.21 mm,精度提高了66%,可以看出,傅里叶级数对动态GM (1, 1) 模型进行修正的方法,可以明显提高模型的预测精度。
| 表 3 两种模型精度对比 Table 3 Accuracy Comparison of Two Models |
 |
3 结束语
本文使用傅里叶级数对观测值中除去趋势项后剩余的残差部分进行拟合,得出用于修正动态GM (1, 1) 模型的残差。通过比较傅里叶级数修正的动态GM (1, 1) 模型和普通的动态GM (1, 1) 模型的预测精度,得出傅里叶级数修正的动态GM (1, 1) 模型的预测精度更高,这种修正方法用于GM (1, 1) 模型进行沉降值的分析预测中,可以提高模型的预测精度。
| [1] | 陈超, 张献州, 尚金光. 高速铁路沉降观测数据生产过程质量控制与管理[J]. 高速铁路技术, 2011, (5): 25–29. |
| [2] | 邓聚龙. 灰色预测与决策[M]. 武汉: 华中理工大学出版社, 1987. |
| [3] | 王利, 张双成, 李亚红. 动态灰色预测模型在大坝变形监测及预报中的应用研究[J]. 西安科技大学学报, 2005, 25(3): 328–332. |
| [4] | 刘思峰, 郭天榜, 党耀国, 等. 灰色系统理论及其应用[M]. 2版. 北京: 科学出版社, 1999. |
| [5] | 孙鹤泉. 实用Fourier变换及C++实现[M]. 北京: 科学出版社, 2009. |
| [6] | 冷建华. 傅里叶变换[M]. 北京: 清华大学出版社, 2004. |
| [7] | 李富荣. 改进的动态GM (1, 1) 模型在人口预测中的应用[J]. 统计与决策, 2013, (19): 72–74. |
| [8] | Kayacan E, Ulutas B, Kaynak O. Grey System Theory-based Models in Time Series Prediction[J]. Expert Systems with Applications, 2010, 37(2): 1784–1789. DOI: 10.1016/j.eswa.2009.07.064 |
 2017, Vol. 42
2017, Vol. 42

