| 社会调查的空间抽样方法研究 |
2. 地球空间信息技术协同创新中心, 湖北 武汉, 430079;
3. 武汉大学社会学系, 湖北 武汉, 430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China;
3. Department of Sociology, Wuhan University, Wuhan 430079, China
抽样是将总体集按某种规律划分为样本集且不损失总体主要信息的方法,是社会调查的前期手段。合理的抽样是一种经济、快速、及时、质量好并且准确性高的调查方式[1, 2]。通过科学的抽样方法确定被调查样本,使样本更具有代表性,从而达到优化调查结果的目的。抽样调查是地理研究、资源评估、环境问题研究和社会经济问题研究的重要手段。信息时代背景下,抽样方法不仅抽样数据量大,还是一种在当前信息技术的支撑下,完成从大量、快速、复杂、多源的信息中提取有用价值的技术处理手段[3]。社会调查数据往往具有空间相关性,发展考虑空间相关性的社会调查空间抽样方法具有重要意义。
空间抽样的主要目的是在二维或三维空间采样[4],其理论是针对地理空间对象的,是对具有空间相关性的各种资源和调查对象进行抽样设计的基础[5]。不同的采样策略对最终的结果将会有很大影响。利用合理的空间抽样方法可以得出科学的采样结果,同时可以使用较少的样本量获得较高精度的统计推断结果。设计一个好的空间抽样模型,可以优化样本的选择,为社会调查、大范围分区调查、多项目综合调查等提供科学依据[6]。
GIS技术的应用领域从现代测绘、国防军事、野外数据采集等自然科学领域,逐步扩展到社会调查、历史、文化等社会学领域[7],利用GIS技术辅助传统的抽样方法,是当前空间人文社会学的一个重要研究课题。
空间抽样领域已有不少成果,例如李连发等提出空间抽样优化决策模型[8]。王劲峰等提出“三明治”空间抽样模型[9]。高丽玲等以厦门岛住区问卷调查的需求为目标,平衡抽样精度和抽样成本,采用简单随机抽样、空间分层抽样和三明治空间抽样方法进行抽样,为厦门岛住区问卷调查选点提供依据[10]。林珲等讨论了人文学与社会科学研究对于空间综合方法的需求[11]。空间抽样目前在社会调查抽样中的应用还很少。现有的空间抽样方法需要布样,在抽样区域内,根据抽样条件,确定样本点位置,样本的选择具有随机性,没有待抽取样本位置固定因素的干扰。空间抽样结果的代表性和地理空间分布的均衡性[12]是决定空间抽样方案的重要指标。空间分布均衡性在抽样中指,各样本之间离散程度大,空间相关性小,各样本受周边其他样本的影响尽可能小,样本分布模式尽可能接近随机或离散模式。从而尽可能保证样本的选取受空间位置影响小,尽可能用少量的样本代表全部区域,从而增加样本的代表性。针对目前社会调查的抽样方法的不足,本文探讨了利用GIS技术对抽样结果进行空间展示并评价其地理空间分布的均衡性,同时实现了相关功能的软件开发。
本文以2014年“武汉市社会状况综合调查(China Social Survey Research in Wuhan)”的数据为基础进行研究。这次调查以武汉市居民为总体,采用多阶段抽样方式。以家庭户为单位,随机抽取2 000个样本,覆盖全市63个社区/居委会。
1 抽样流程传统的抽样方法,分为简单随机抽样、分层抽样、整群抽样、系统抽样[13]等。社会调查中常用的抽样方法为在抽样框的限定条件下,利用随机数表根据被抽取对象的ID进行随机数匹配抽样。本文从全武汉市978万人口(2011年统计数据)中抽取2 000个人口为调查样本,在随机抽样的基础上制订了一个新的抽样流程,为社会调查做数据储备。抽样流程如图 1所示。
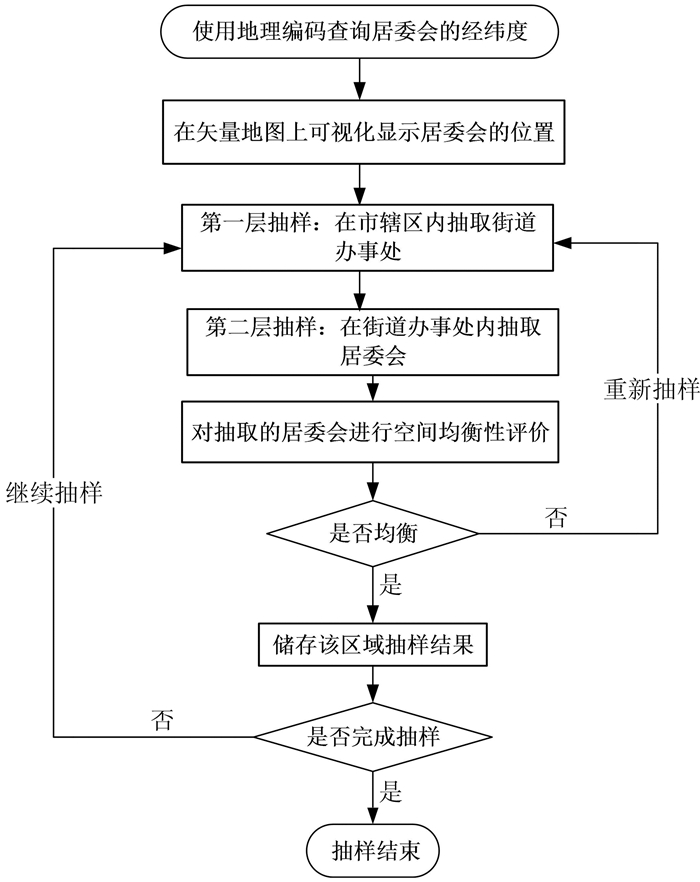 |
| 图 1 抽样流程图 Fig.1 Flow Chart of Sampling |
1.1 抽样数据预处理
根据湖北省统计局提供的截至到2011年的人口普查数据,获得武汉市13个市辖区下属186个街道办事处包含的3493个社区/居委会名称、包含人口数、户数、男性人数、女性人数及13区代码和街道办事处代码。
通过调用百度Geocoding API,进行地理编码,主要步骤包括地址标准化、地址匹配和地址量化。对于编码模型和标准,使用了百度地图提供的模型、词典、数据库以及量化规则。地址编码的过程在API的协助下变得快捷简便,通过调用API,发送地址请求给服务器,服务器接收后返回该地址对应的地理坐标。
完成初步地理编码后,通过已有的数据库和先验知识,制定社区/居委会(以下统称样点)纠偏标准:
① 样点应全部落在武汉市范围内;
② 明确规定属于各市辖区的样点不应越区;
③ 样点不应落在不可能建造社区的地点,如东湖,长江,道路中央,荒野等。
经过查错和纠偏最终获得位置匹配准确的地图。地理编码后的武汉市社区/居委会可视化结果。
1.2 抽样流程为了限定抽样条件和制定抽样规则,首先拟定抽样框。抽样框中包含市辖区代码、13个市辖区名称、每个市辖区包含的户数、户数占总人口的比例,以及分配给每个市辖区的样本数,需要抽取的街道办事处个数,每个市辖区包含的总街道数,每个市辖区应抽到的社区/居委会数量。
本文中抽样方法选取为简单随机抽样[12],也称为单纯随机抽样。从总体N个单元中抽取n个单元作为样本,抽取方法是从总体中逐个不放回地抽取单元,每次都在所有未入样的单元中等概率抽取。简单随机样本也可以一次同时从总体中抽得,只要保证全部可能的样本每个被抽中的概率都相等。
具体抽样步骤如下:
1) 第一层抽样:以市辖区为单位,根据抽样框的要求,采用简单随机抽样方法抽样得到街道办事处;
2) 第二层抽样:在第一层抽样的基础上,以街道办事处为单位,根据抽样框的要求,采用简单随机抽样方法抽样得到居委会;
3) 重复以上抽样步骤,完成13个市辖区的抽样,存储抽样结果,实现在地图上的可视化。
完成抽样后判断样点分布是否合理,需要考虑社区/居委会在空间上产生的空间异质性。空间异质性指的是生态、社会等空间过程和格局在空间分布上的不均匀性及其复杂性,其相对概念为空间均衡性[13]。好的抽样结果要求空间异质性大,空间分布相对均衡。本文使用最邻近指数法对空间分布的均衡性进行评价。根据空间分布均衡性的标准,本文以样点的空间分布模式属于均匀且尽可能更加均匀(即R值尽可能大于1),或趋近于随机模式(即R值尽可能趋近于1)作为判断样点分布合理的依据。
2 空间抽样及抽样结果评价实验 2.1 最优抽样方案由于在已知样点中抽取所需样本会受到样点固定位置的影响,进而影响被抽取样本的分布模式,分别计算武汉市13个市辖区中所有社区/居委会的空间分布模式。
为研究样本点位置固定对抽样结果带来的影响,拟在均匀模式和聚集模式下各选取一个市辖区作为实验区。由于武汉市中心城区为武昌、江汉、硚口、江岸、洪山、青山,同时也是本次社会调查的主要研究区域,即样本分配较多,因此制定实验区的选择标准: ①均匀模式和聚集模式下各选一个有代表性的实验区;②为武汉市中心城区,样本较多。
中心城区中,江汉区和洪山区样点分布为均匀模式,由于洪山区被分配样本更多,故选择洪山区作为实验区。武昌、硚口、江岸、青山均属于聚集模式,其中江岸区在样本分配折衷的情况下聚集模式最明显,故选择江岸区作为实验区。
在抽样框架中,洪山区需抽取的样本个数为8,江岸区需抽取的样本个数为6。为找出在抽样框要求下,两个区域的最优抽样方案,对洪山区进行样本数为8的随机抽样100次,对江岸区进行样本数为6的随机抽样100次,从中找出分布最均匀或相对最接近均匀的一次抽样方案为最优结果。洪山区和江岸区总体样本点分布图如图 2所示。
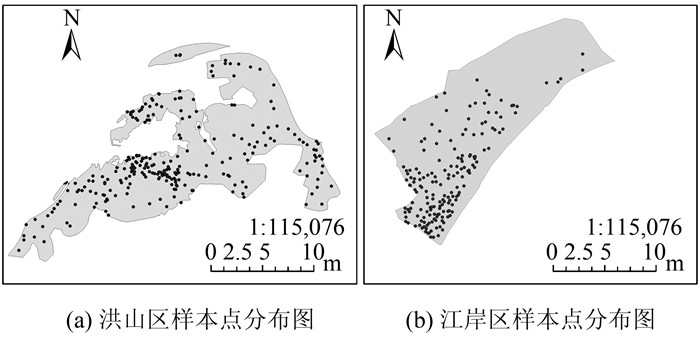 |
| 图 2 洪山区和江岸区样本点分布图 Fig.2 Distribution of Sampling Points in Hongshan District & Jiang'an District |
对于均匀模式,样本点位置对抽样结果带来的影响较小,最优抽样方案需要保证分布均匀,R大于1,且在多次实验中,相对最均匀。对于聚集模式,样本点位置对抽样结果带来的影响比较大,最优抽样方案应尽可能均匀,即在多次实验中,R值相对最大,最趋近均匀模式。
对洪山区和江岸区分别进行100次随机抽样,并计算每一次抽样结果的最邻近指数,得到100次抽样结果的最邻近指数图如图 3所示。
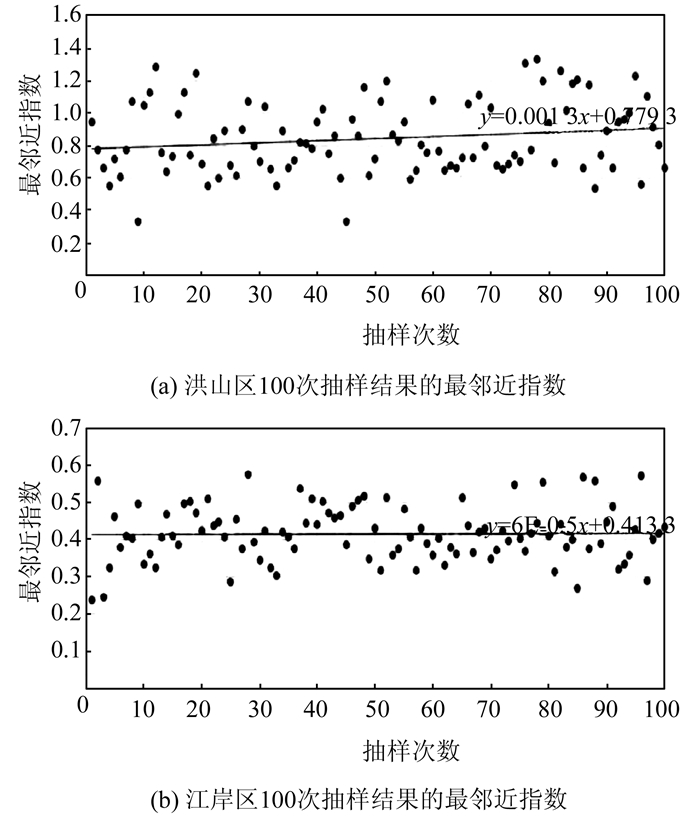 |
| 图 3 洪山区和江岸区100次抽样结果最邻近指数 Fig.3 NNI of 100 Times of Sampling in Hongshan District & Jiang'an District |
选取多次抽样中的最大值作为最后的R值,洪山区R值为1.33,抽样结果分布为均匀模式;江岸区R值为0.58,抽样结果分布虽为聚集模式,但已是多次实验中最趋近于均匀模式的方案,故选取以上两次抽样结果为相对最优结果,抽样结果如图 4所示。
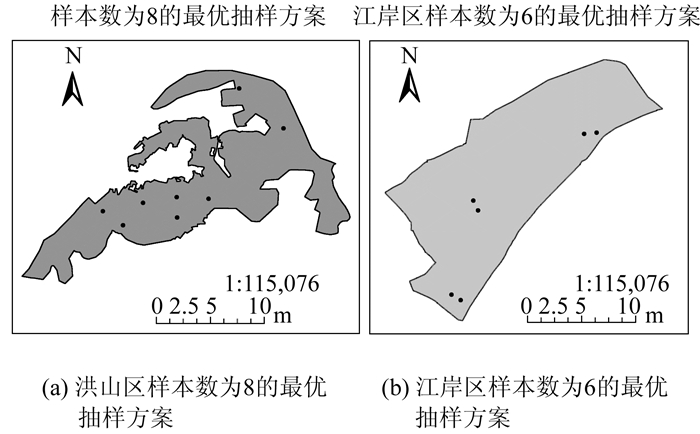 |
| 图 4 洪山区和江岸区的最优抽样方案 Fig.4 The Optimal Sampling Result of Hongshan District & Jiang'an District |
2.2 抽样框改进
对社会调查而言,样本数的选取应考虑两方面因素:①样本数量影响调查成本,样本数量越大调查成本越高。样本数量应在调查成本可控范围内;②样本选取应具有一定的随机性,样本数量应尽量减少抽样成本和次数,即最大概率抽取到符合预期的样本。
不断增加样区的需抽取样本数量进行实验,将抽样结果的最邻近指数置信度设为95%当最邻近指数的置信区间包含分布均匀的标准,即包含1;或最大程度趋近于分布均匀的标准,即趋近1时,需抽取的样本数为最合适的样本数。
对洪山区需抽取样本数为8和江岸区需抽取样本数为6分别进行的100次抽样得到的最邻近指数散点图进行一元线性回归分析,在置信度为95%的情况下,得到置信区间如表 1所示。
| 表 1 洪山区和江岸区抽样结果的NNI置信区间 Tab.1 Confidence Interval of NNI of Sampling Result for Hongshan District & Jiang'an District |
 |
表 1说明,洪山区抽样结果的最邻近指数有95%的可能性落在置信区间[0.692, 0.866],不满足分布均匀的条件,同时也小于洪山区所有社区/居委会分布R值,故该方案下的综合抽样结果的代表性不强;江岸区抽样结果的最邻近指数有95%的可能性落在置信区间[0.306, 0.386],不满足分布均匀的条件,同时也小于江岸区所有社区/居委会分布R值,故该方案下的综合抽样结果的代表性不够。初步分析由于样本数目较少,而导致抽样结果满足分布均匀的可能性较低,增加了抽样的成本。
为提高被抽取样本为均匀分布的可能性,减少抽样样本,逐步增加样本个数进行实验。由于抽样分两层,第二层抽样在第一层抽样基础上在每个街道办事处内抽取两个居委会,故增加的抽样个数为偶数增加。
对于样本点分布均匀,抽样结果受影响较小的洪山区,经过多次实验,发现当样本数分别为8、12、16时得到的抽样统计结果较为具有代表性,抽样结果的最邻近指数置信区间如表 2所示。
| 表 2 不同样本数洪山区抽样结果的NNI置信区间 Tab.2 Confidence Interval of NNI of Different Sampling Results in Hongshan District |
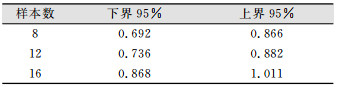 |
由表 2可知,对于样本点分布均匀,抽样结果受影响较小;当抽取样本数增加时,被抽样本最邻近指数的置信度区间也越往1靠近。当被抽样本数为16时,置信区间已经包含1,抽样结果的最邻近指数有95%的可能性落在置信区间[0.868, 1.011],最大限度逼近均匀分布。考虑样本被调查需要的抽样成本和调查成本,综合判断对于洪山区,抽样数定为16为最佳,在节约调查成本的前提下,抽样结果分布均匀。对样本总体的代表性最大化,样本的调查结果更具代表性。
对于样本点分布聚集,抽样结果受影响较大的江岸区,经过多次实验,发现当样本数分别为14、16、18时得到的抽样统计结果较为具有代表性,抽样结果的最邻近指数置信区间如表 3所示。
| 表 3 不同样本数江岸区抽样结果的NNI置信区间 Tab.3 Confidence Interval of NNI of Different Sampling Results in Jiang'an District |
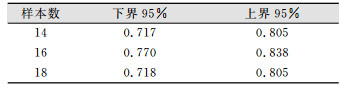 |
由表 3可知,对于样本点分布聚集,抽样结果受影响较大的情况,当抽取样本数增加时,被抽样本最邻近指数的置信度区间在样本数为16时达到峰值。可能是因为样本点分布过于聚集,当被抽取样本数目过大,多数被抽取的样本属于分布聚集的区域,导致抽样结果反而分布聚集。由表 3可知,当被抽样本数为16时,抽样结果的最邻近指数有95%的可能性落在置信区间[0.770, 0.838],最大限度逼近均匀分布。考虑样本被调查需要的抽样成本和调查成本,综合判断对于江岸区,抽样数定为16为最佳,在节约调查成本的前提下,抽样结果分布均匀。对样本总体的代表性最大化,样本的调查结果更具代表性。
3 社会调查空间抽样软件的设计与开发社会调查空间抽样软件采用C#+ArcGIS Engine的开发模式,将抽样流程软件化,实现抽样结果在软件界面的空间可视化,将抽样结果导出为文本格式进行存储,计算抽样结果的空间分布均衡性,判断抽样结果是否符合标准。抽样结果的可视化界面及抽样结果的分析界面分别如图 5(a)、5(b)所示。
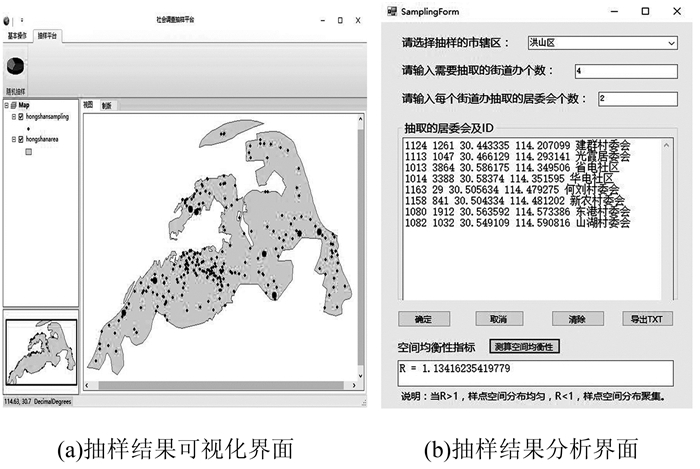 |
| 图 5 空间抽样软件界面 Fig.5 Interface of Spatial Sampling Software |
4 结束语
传统的社会调查抽样方法是在抽样框条件限定下借助随机数表抽取样本,本文提出的社会调查空间抽样流程对比传统方法,实现了高效、准确的抽样,提高了抽样效率,减少了抽样成本,实现了抽样结果的空间可视化,并在空间均衡性评价的辅助下确认抽样结果是否具有代表性,辅助选取最优抽样结果。在提高抽样效率与结果合理性的同时,实现了GIS与传统社会学的对接,对于GIS技术应用于社会学领域进行了初步尝试。本文方法还需要进一步优化,须引入多种空间均衡性评价方法进行对比分析,从而提出更加科学的空间抽样和均衡性评价方法。
| [1] |
Cochran W G. Sampling Techniques[M]. 3rd ed. New York: John Wiley & Sons, 1977.
|
| [2] |
Kish L. Survey Sampling[M]. New York: John WiJey & Sons, 1985.
|
| [3] |
边馥苓, 杜江毅, 孟小亮. 时空大数据处理的需求、应用与挑战[J]. 测绘地理信息, 2016, 41(6): 1-4. |
| [4] |
Wang Jinfeng, Stein A, Gao Binbo, et al. A Review of Spatial Sampling[J]. Spatial Statistics, 2012, 2(1): 1-14. |
| [5] |
姜成晟, 王劲峰, 曹志冬. 地理空间抽样理论研究综述[J]. 地理学报, 2009, 64(3): 368-380. DOI:10.3321/j.issn:0375-5444.2009.03.012 |
| [6] |
连健. 基于GIS的抽样框编制与抽样技术方法研究[D]. 北京: 首都师范大学, 2008
|
| [7] |
曾庆伟. 论GIS在社会经济领域中的运用[J]. 中南财经政法大学学报, 2005(3): 23-27. DOI:10.3969/j.issn.1003-5230.2005.03.004 |
| [8] |
李连发, 王劲峰, 刘纪远. 国土遥感调查的空间抽样优化决策[J]. 中国科学(D辑)地球科学, 2004, 34(10): 975-982. |
| [9] |
王劲峰, 姜成晟, 李连发. 空间抽样与统计推断[M]. 北京: 科学出版社, 2009.
|
| [10] |
高丽玲, 李新虎, 王翠平. 空间抽样的理论方法与应用分析———以厦门岛问卷调查为例[J]. 地球信息科学学报, 2010, 12(3): 358-364. |
| [11] |
林珲, 赖进贵, 周成虎. 空间综合人文学与社会科学研究[M]. 北京: 科学出版社, 2010.
|
| [12] |
Glaeser E L. Cities, Agglomeration and Spatial Equilibrium[J]. Oup Catalogue, 2008, 88(3): 693-694. |
| [13] |
冯士雍, 倪加勋, 邹国华. 抽样调查理论与方法(第二版)[M]. 北京: 中国统计出版社, 2012.
|
 2018, Vol. 43
2018, Vol. 43


