| 基于CryoSat-2 SARIn数据的南极Grove山地区DEM建立和分析 |
南极作为冰冻圈的重要组成部分,与全球气候变化有着紧密的联系[1-3]。而数字高程模型(digital terrain model, DEM)是在极地从事各项科学研究最基础的地理信息数据。在过去几十年,各国学者基于不同类型的卫星数据构建了多个南极DEM,但因为数据源的差异,其分辨率和高程精度也各不相同,且在南极陡峭地区和边缘地区高程精度较低[4-6]。
2010年,欧州太空局(European Space Agency, ESA)成功发射了主要用于监测全球陆地冰川和海冰厚度的Ku波段雷达测高卫星CryoSat-2(Cryosphere Satellite 2),其搭载的合成孔径干涉雷达高度计为不同地形提供了不同的观测模式。相较于传统高度计,CryoSat-2因其大轨道倾角和小轨迹间距的设计,使其拥有更大的数据覆盖范围以及更高的数据覆盖密度。自CryoSat-2卫星发布以来,已有多位学者基于CryoSat-2测高数据生成了全南极DEM,并与已有DEM及地形数据进行比较,分别验证了其整体精度[7-9]。传统的雷达测高卫星往往假定最近回波点(point of closest approach,POCA)源于星下点,无法对地形起伏较大的南极边缘区域进行精确地测量。而CryoSat-2 SARIn(SAR interferometric)模式则利用差分相位精确地确定回波点的位置,提高了雷达高度计对于南极边缘区域的观测精度。相较于CryoSat-2 L2数据的单一POCA高程点,SARIn模式数据干涉处理能得到远多于L2数据的高程点结果,从而可生成更高分辨率的DEM,更好地体现细微地形[10-13]。
格罗夫山(Grove)是中国南极科学考察的重点区域,高精度、高分辨率的DEM是在此处开展地质、冰川学等研究的基础。本文基于CryoSat-2 SARIn模式L1b数据,利用干涉处理方法建立南极Grove山地区的DEM,并与CryoSat-2 L2高程脚点数据及常用的南极DEM进行比较。对比最终生成的DEM与参考DEM之间差异,对可能的误差来源进行分析。
1 实验数据和原理Grove山地区位于东南极中山站至昆仑站科考沿线的裸露岛峰群,距中山站约400 km。其主要覆盖范围为73°40′E~76°00′E,72°15′S~73°15′S间约8 000 km2的区域,如图 1所示。Grove山地区是中国东南极科考的重点区域,目前已在该地区陆续开展了多次内陆考察。
 |
| 图 1 Grove山地区示意图 Fig.1 The Grove Mountains Area in East Antarctica |
相较于L1级数据,SARIn模式L1b数据已经完成合成孔径和脉冲压缩等基本步骤,可直接用于干涉处理。CryoSat-2 L2数据在L1/L1b数据基础上经过了波形重跟踪处理,并对重跟踪获取的测距信息进行改正,最终得到脚点高程。本文采用的CryoSat-2 SARIn模式基线C数据时间范围为2016-01~12。
为验证最终结果,选取南极常用的精度较高的DEM作为参考。考虑到DEM的不同数据源对产品精度的影响,本文选用ICESat DEM(激光测高)[14]、Bamber DEM(雷达和激光测高融合)[15]、REMA(光学)[16]、TanDEM-X DEM(SAR)[6]4种DEM作为验证DEM。
区别于传统星载SAR的单天线接收信号模式,SARIn模式采用一发双收来接收回波信号,两天线相距1 m。图 2为CryoSat-2 SARIn模式测量的基本原理。图中,O1和O2分别为两天线的位置;B为基线长;地面上两地物点为P1和P2,这里假定P1为星下点,P2为最近回波点(POCA);两幅天线到POCA点的距离分别为R1和R2,距离差为ΔR;局部坡度角为α。对于任一非星下点的目标产生的回波,双天线接收到的信号存在距离差ΔR,这一差异会表现在两者相位上。利用双天线对同一地物的回波相位差反推回波倾角就可以计算出回波点的位置。
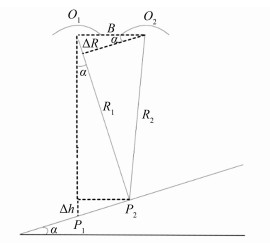 |
| 图 2 CryoSat-2 SARIn模式测量基本原理 Fig.2 Fundamental of CryoSat-2 Synthetic Aperture Interferometric Mode |
根据相位与距离的关系,可以表示回波点到两天线的距离差ΔR,即:
| $ \Delta R = \frac{\lambda }{{2\pi }}\Delta \varphi $ | (1) |
式中,Δφ为两天线接收到回波点信号的相位差;λ为波长。
通过图中几何关系,并结合式(1)即可推导出回波倾角:
| $ \alpha = \arcsin \left( {\frac{\lambda }{{2\pi \times B}} \times \Delta \varphi } \right) $ | (2) |
一旦回波倾角α确定,那么根据CryoSat-2的星历参数和雷达高度计的距离测量值,就可以计算出P2点的位置。
参考传统InSAR提取表面地形的步骤,考虑到CryoSat-2非成像雷达的特性,以及固定的天线基线长度,SARIn模式干涉处理提取DEM主要包括数据滤波、相位解缠和地理编码[11-13]。
2 数据处理和结果自CryoSat-2发射升空至今,ESA基于基线标识先后发布了3个版本的数据,分别为基线A(Baseline-A)、基线B(Baseline-B)和基线C(Baseline-C)。尽管基线C数据在原数据基础上进行了卫星姿态的优化,增加了初始补偿,但是笔者在研究中发现其姿态仍然存在问题,特别是侧滚角误差对结果影响较大[12, 17]。因此利用CryoSat-2 SARIn L1b数据干涉处理提取DEM前需要进行姿态校正。
2.1 CryoSat-2姿态校正假设局部区域在短时间内没有高程变化,那么该时间段内升降轨数据和参考DEM的平均高程差异(mean elevation difference,MED)理论上应该近似相等,但侧滚角误差的存在会对升降轨数据有不同的影响,导致高程出现误差。以该实验区内CryoSat-2 SARIn模式L1b升降轨数据各5条为试验数据,利用干涉处理方法提取高程,然后与参考DEM求取差值。如图 3(a),可以发现升(蓝色)、降(红色)轨数据和参考DEM的MED存在明显差异。而人为对L1b数据中侧滚角分别进行±0.005°和±0.007°的初始补偿后重新计算高程差值,则发现升降轨之间MED差异减小,趋于相等。如图 3(b)所示,各曲线分别表示升降轨数据进行一定侧滚角补偿后和参考DEM高程差异的拟合曲线。基于此发现,说明尽管基线C数据相对于基线B数据已经对卫星姿态进行了修正,但现有姿态仍然存在问题。为验证侧滚角的具体偏差,利用该区域内升降轨各5条数据分别取[-0.01°,0.020°]之间10个初始侧滚角补偿,进行补偿后的DEM提取实验。基于升降轨数据和参考DEM的平均高程差异应该近似相等的前提(即图 3(c)中相应的升降轨交点),可以求得实验区内CryoSat-2数据侧滚角偏差σRoll∈[0.007°, 0.020°],如图 3(c)蓝色区域所示。图 3(c)中加粗实线表示5条升降轨数据平均值。而ESA于2018年才发现此问题,并紧急发布了修正数据(star tracker mispointing angles dataset)。侧滚角更正前后如图 3(d)所示,细线为修正前的08-01和08-03单条轨道部分数据的侧滚角值,粗线为修正之后的侧滚角值,部分区域有超过0.020°的偏差。基于此数据,本文重新修正了L1b数据中的侧滚角参数。
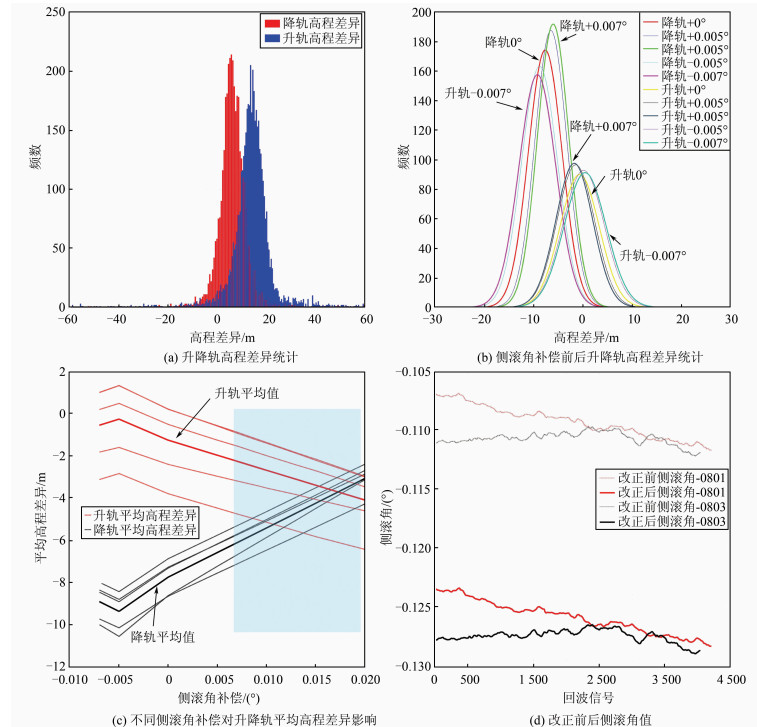 |
| 图 3 CryoSat-2数据侧滚角偏差及改正 Fig.3 Bias and Correction of Roll Angle in CryoSat-2 Data |
2.2 SARIn模式干涉处理提取DEM结果
根据SARIn模式干涉处理原理,利用2016-01~12的CryoSat-2 SARIn模式L1b数据处理生成了Grove山地区高程点(图 4(b)),相较于ESA提供的L2数据(图 4(a)),其数据量提高约50~70倍。数据量的提高可以呈现更精细的局部地形,同时在一定程度上减少了高程点内插带来的误差。由于最终生成的仅是高程点,需要进一步内插生成DEM栅格。研究表明,相较于三角格网、最小曲率和距离反权等插值方法,克里金插值在南极有着更好的可靠性和鲁棒性[18, 19]。但克里金插值法的搜索半径以及变异函数的选择都会对结果存在影响,较小的搜索半径能够得到更优的插值结果,但是也会导致最终栅格的空洞增多,所以需要平衡两者的关系。本文采用克里金插值生成DEM时搜索半径选取为1 km。图 4(c)为CryoSat-2 L1b数据干涉处理生成的高程点最终的内插结果,参考基准为WGS-84椭球,采用极方位立体投影,插值后DEM的分辨率为200 m。
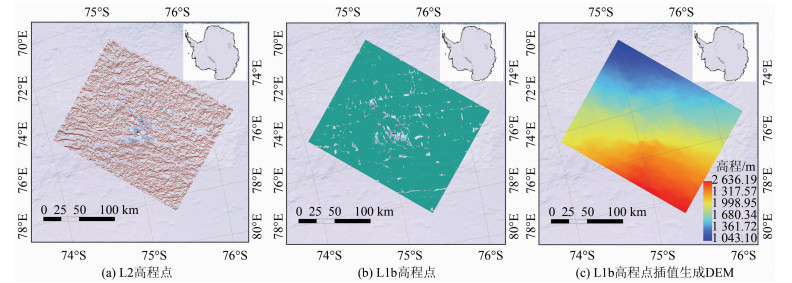 |
| 图 4 CryoSat-2 SARIn干涉处理提取DEM结果 Fig.4 CryoSat-2 Swath Processed DEM |
3 干涉处理提取DEM结果分析 3.1 SARIn模式干涉处理提取DEM精度分析
为了验证SARIn模式干涉处理最终生成的DEM(CryoSat-2 Swath Processed DEM,CS2-SW DEM)的高程精度,首先以ESA提供的L2高程点插值生成的DEM(CS2-L2 DEM)为比较数据,研究CS2-SW DEM和CS2-L2 DEM相对于TanDEM-X DEM的差异。由于L2数据高程脚点较少,插值生成的CS2-L2 DEM的分辨率设为1 km。如图 5所示高程差值直方图,CS2-SW DEM和TanDEM-X DEM高程差异为0.23±4.29 m,高程差异小于10 m的数据约占96.8%。而CS2-L2 DEM和TanDEM-X DEM高程差异为-2.24±8.50 m,高程差异小于10 m的数据仅占89.2%,仍存在约5%的数据和TanDEM-X DEM高程差异大于20 m。
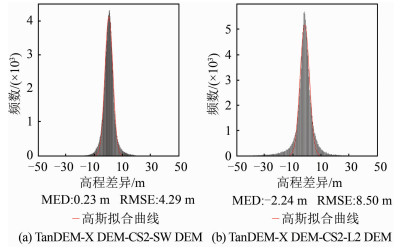 |
| 图 5 CS2-SW DEM和CS2-L2 DEM与TanDEM-X DEM高程差异统计直方图 Fig.5 Histogram of Difference of CS2-SW DEM/CS2-L2 DEM and TanDEM-X DEM |
以4种常用的DEM(ICESat DEM、Bamber DEM、REMA和TanDEM-X DEM)为参考DEM,均利用本文结果减去参考DEM的高程值,得到CS2-SW DEM和参考DEM高程差异的统计直方图(图 6)。从图 6可以看出,4个高程差异直方图均呈现较标准的正态分布。CS2-SW DEM与TanDEM-X DEM有着最好的一致性,与REMA的结果也较为符合,两者整体高程差异为分别为-0.28±4.68 m和-3.57±4.71 m。而CS2-SW DEM与ICESat DEM和Bamber DEM的符合程度较差,整体差异较大,分别为-3.67±12.64 m和-4.90±10.86 m。这一差异一方面是由于该区域内数据源时间不一致,另一方面是因为Bamber DEM和ICESat DEM相较于REMA和TanDEM-X DEM是利用高程点插值生成,所以存在插值误差。SARIn干涉处理方法得到结果由于数据量优势,能有效减少插值误差,从而和TanDEM-X DEM和REMA的结果更为接近。图 6(c)和图 6(d)中,高程差异分布集中,基本分布于±10 m之间,分别占整体数据的91.6%和93.3%。对比CS2-SW DEM与REMA和TanDEM-X DEM的结果发现,与REMA的平均高程差异为-3.57 m,远大于与TanDEM-X DEM的平均高程差异-0.28 m,且这一差异和与ICESat DEM的平均高程差异-3.67 m相近。排除参考DEM本身精度差异,这一误差主要由雷达穿透引起,而光学和激光雷达生成的DEM为冰表面高程。
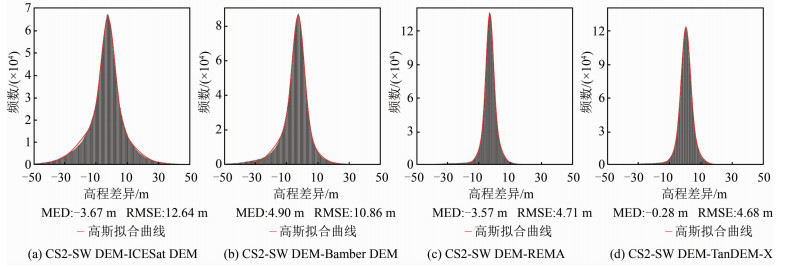 |
| 图 6 CS2-SW DEM和参考DEM高程误差统计直方图 Fig.6 Histogram of Difference Between the CS2_SW DEM and Reference DEM |
考虑到干涉处理生成DEM原理中对局部坡度的要求,可以看出DEM高程精度与坡度有着密切关系。按照0.1°坡度间隔统计了CryoSat-2干涉处理高程点与TanDEM-X DEM高程差异的分布情况,并计算了每个坡度间隔内的误差,结果如图 7所示。随着坡度的增加,均方根误差单调递增。虽然CryoSat-2引入SARIn模式加强了对陡峭地区的测量,但坡度仍会引起测量误差,且这一误差仍是雷达高度计测量误差的主要来源之一。但是平均高程差异是先减小再上升,这与SARIn模式干涉处理原理相吻合,因为合适的局部坡度能导致双天线接收到的回波信号呈现高相干性。
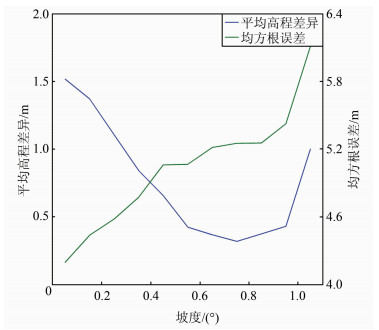 |
| 图 7 CryoSat-2干涉处理高程点与TanDEM-X DEM高程差异按坡度统计图 Fig.7 Comparison of CryoSat-2 Swath Processed Points with TanDEM-X DEM as a Function of Surface Slope |
3.2 CryoSat-2穿透影响
对于CryroSat-2 Ku波段信号来说,其对介质的穿透效应不能忽视,所以CS2数据最终生成的DEM会因为雷达穿透而存在误差。雷达穿透深度,实际上定义为雷达信号在介质内部辐射强度降至材料表面原始值的e-1(约37%)的深度[20]。根据比尔-朗伯定律,介质内部的电磁波强度从表面呈指数下降,即:
| $ I(z) = {I_0}{{\rm{e}}^{ - \alpha z}} $ | (3) |
式中,I0为电磁波在材料表面的初始强度;α为消光系数,与电磁波在介质中散射系数(Ks)和吸收系数(Ka)有关;z为电磁波进入介质的深度。所以穿透深度δp可以表示为:
| $ {\delta _p} = \frac{1}{\alpha } = \frac{1}{{{K_s} + {K_a}}} $ | (4) |
Mätzler[21]给出了散射系数和吸收系数的公式:
| $ {K_s} = \frac{{3p_c^3{k^4}}}{{32}}v \times (1 - v){\left| {\frac{{2\varepsilon ' - 1}}{{2\varepsilon ' + \varepsilon _i^\prime }}} \right|^2} $ | (5) |
| $ {K_a} = k \times \frac{{\varepsilon" }}{{\sqrt {\varepsilon '} }} $ | (6) |
式中,
由于缺少实验区域的实测数据,因此本研究仅将ERA再分析资料在该区域内的平均值作为各参数的估计值。其中雪平均温度约-6.61 ℃,积雪密度约0.35 g/cm3。由于Grove山地区位于南极冰盖靠内陆区域,所以雪粒径以粒雪的粒径(约1 mm)为参考。根据上述原理,可以得到不同频率的雷达信号在不同液态水含量情况下的穿透深度,如图 8所示。当积雪为湿雪状态,即液态水体积分数大于0时,CryoSat-2的穿透深度大约在0.7~3.0 m左右,这符合CS-SW DEM与REMA及ICESat DEM的平均高程差异。
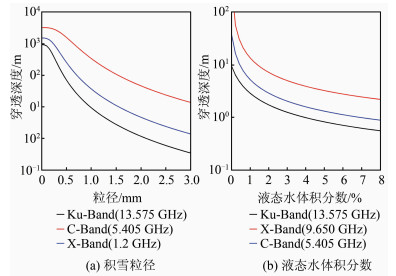 |
| 图 8 不同波段在不同积雪属性下的积雪穿透深度 Fig.8 Penetration Depth for Different Bands in Snow as a Function of Grain Size and Liquid-Water Content |
4 结束语
本文基于CryoSat-2 SARIn模式L1b数据,利用干涉处理方法生成了南极Grove山地区DEM。针对数据处理中发现的CryoSat-2姿态问题进行了讨论,并利用ESA最新发布的姿态补偿数据进行了校正。同时和CryoSat-2 L2数据产品及现有的4种常用南极DEM进行了高程比较,就雷达穿透引起的高程差异进行了分析。
1) CryoSat-2基线C数据卫星姿态仍然存在误差,特别是侧滚角,所以进行SARIn模式L1b基线C数据干涉处理时,需要进行侧滚角的改正以提高最终的高程精度。
2) CryoSat-2 SARIn模式数据干涉处理生成的高程点远多于L2数据产品,从而有效减少插值误差并更好地呈现地形细节信息,这一优势通过与常用南极DEM的比较也能看出。CS2_SW DEM与REMA和TanDEM-X DEM的整体高程差异较小。其中和REMA的高程差异主要由穿透引起,约0.7~3.0 m。
3) 干涉处理方法提取的CryoSat-2脚点高程精度随着坡度的增加而降低,但是和TanDEM-X DEM的平均高程差异会随着坡度的增加先减小后增加。
致谢:感谢欧州太空局免费提供的CryoSat-2数据,感谢明尼苏达大学免费提供的全南极DEM (REMA)、德国航空航天中心免费提供的TanDEM-X DEM以及美国国家冰雪数据中心提供的Bamber DEM和ICESat DEM。
| [1] |
Mercer J H. West AntarcticIce Sheet and CO2 Greenhouse Effect: A Threat of Disaster[J]. Nature, 1978, 271(5643): 321-325. DOI:10.1038/271321a0 |
| [2] |
Rott H, Skvarca P, Nagler T. Rapid Collapse of Northern Larsen Ice Shelf, Antarctica[J]. Science, 1996, 271(5250): 788-792. DOI:10.1126/science.271.5250.788 |
| [3] |
Zwally H J, Giovinetto M B, Li J, et al. Mass Changes of the Greenland and Antarctic Ice Sheets and Shelves and Contributions to Sea-Level Rise: 1992-2002[J]. Journal of Glaciology, 2005, 51(175): 509-527. DOI:10.3189/172756505781829007 |
| [4] |
Liu Hongxing, Jezek K C, Li Biyan. Development of an Antarctic Digital Elevation Model by Integrating Cartographic and Remotely Sensed Data: A Geographic Information System Based Approach[J]. Journal of Geophysical Research: Solid Earth, 1999, 104(10): 23199-23213. |
| [5] |
Fricker H A, Borsa A, Minster B, et al. Assessment of ICESat Performance at the Salar De Uyuni, Bolivia[J]. Geophysical Research Letters, 2005, 32(21): 1-5. |
| [6] |
Rizzoli P, Martone M, Gonzalez C, et al. Generation and Performance Assessment of the Global TanDEM-X Digital Elevation Model[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 132: 119-139. DOI:10.1016/j.isprsjprs.2017.08.008 |
| [7] |
Helm V, Humbert A, Miller H. Elevation and Elevation Change of Greenland and Antarctica Derived from CryoSat-2[J]. The Cryosphere, 2014, 8(4): 1539-1559. DOI:10.5194/tc-8-1539-2014 |
| [8] |
Slater T, Shepherd A, McMillan M, et al. A New Digital Elevation Model of Antarctica Derived from CryoSat-2 Altimetry[J]. The Cryosphere, 2018, 12(4): 1551-1562. DOI:10.5194/tc-12-1551-2018 |
| [9] |
李斐, 肖峰, 张胜凯, 等. 基于CryoSat-2测高数据的全南极冰盖DEM的建立与精度评估[J]. 地球物理学报, 2017, 60(5): 1617-1629. |
| [10] |
Hawley R L, Shepherd A, Cullen R, et al. Ice-Sheet Elevations from Across-Track Processing of Airborne Interferometric Radar Altimetry[J]. Geophysical Research Letters, 2009, 36(22): 297-304. |
| [11] |
Gray L, Burgess D, Copland L, et al. Interferometric Swath Processing of Cryosat Data for Glacial Ice Topography[J]. The Cryosphere, 2013, 7(6): 1857-1867. DOI:10.5194/tc-7-1857-2013 |
| [12] |
Gourmelen N, Escorihuela M J, Shepherd A, et al. CryoSat-2 Swath Interferometric Altimetry for Mapping Ice Elevation and Elevation Change[J]. Advances in Space Research, 2017, 62(6): 1226-1242. |
| [13] |
董玉森, 张奎, 马娇, 等. CryoSat-2 SARIn数据干涉处理及DEM获取[J]. 武汉大学学报·信息科学版, 2017, 42(6): 803-809. |
| [14] |
DiMarzio J, Brenner A, Schutz R, et al. GLAS /ICESat 500 m Laser Altimetry Digital Elevation Model of Antarctica[DB/OL].[2013-09-18]. http://nsidc.org/data/docs/daac/nsidc0304_0305_glas_dems.gd.html
|
| [15] |
Bamber J L, Gomez-Dans J L, Griggs J A. A New 1 km Digital Elevation Model of the Antarctic Derived from Combined Satellite Radar and Laser Data-Part 1: Data and Methods[J]. The Cryosphere, 2009, 3(1): 101-111. DOI:10.5194/tc-3-101-2009 |
| [16] |
Howat I M, Porter C, Smith B E, et al. The Reference Elevation Model of Antarctica[J]. The Cryosphere, 2019, 13(2): 665-674. DOI:10.5194/tc-13-665-2019 |
| [17] |
Gray L, Burgess D, Copland L, et al. A Revised Calibration of the Interferometric Mode of the CryoSat-2 Radar Altimeter Improves Ice Height and Height Change Measurements in Western Greenland[J]. The Cryosphere, 2017, 11(3): 1041-1058. DOI:10.5194/tc-11-1041-2017 |
| [18] |
袁乐先, 李斐, 张胜凯, 等. 基于ICESat数据的南极冰盖DEM插值方法比较及精度分析[J]. 冰川冻土, 2015, 37(4): 946-953. |
| [19] |
张胜凯, 肖峰, 李斐, 等. 基于CryoSat-2测高数据的南极局部地区DEM的建立与精度评定[J]. 武汉大学学报·信息科学版, 2015, 40(11): 1434-1439. |
| [20] |
Ulsaby F T, Stiles W H, AbdelRazik M. Snowcover Influence on Backscattering from Terrain[J]. IEEE Transactions on Geoscience and Remote Sensing, 1984, 22(2): 126-133. |
| [21] |
Mätzler C. Improved Born Approximation for Scattering of Radiation in a Granular Medium[J]. Journal of Applied Physics, 1998, 83(11): 6111-6117. DOI:10.1063/1.367496 |
| [22] |
Tiuri M, Sihvola A, Nyfors E G, et al. The Complex Dielectric Constant of Snow at Microwave Frequencies[J]. IEEE Journal of Oceanic Engineering, 1984, 9(5): 377-382. DOI:10.1109/JOE.1984.1145645 |
| [23] |
Mätzler C. Applications of the Interaction of Microwaves with the Natural Snow Cover[J]. Remote Sensing Reviews, 1987, 2(2): 259-387. |
 2020, Vol. 45
2020, Vol. 45

