| 变形监测数据小波去噪分解尺度确定方法 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079;
3. 河北电力工程监理有限责任公司,河北 石家庄,050021
2. Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China;
3. Hebei Electric Power Engineering Supervision Co., Ltd., Shijiazhuang 050021, China
受测量仪器、测量方法及外界环境条件等因素的综合影响,测量数据中难免会存在噪声,为此有必要对实测数据进行去噪处理,以确保高质量的数据成果。小波分析因其良好的时频局部性及多分辨分析能力,在数据去噪方面得到了广泛应用[1-3]。小波去噪的分解尺度选择对去噪效果尤为重要,但在实际数据处理中,测量数据的真值未知,无法准确确定最佳的分解尺度。因此,如何选择合适的小波去噪分解尺度方法是小波去噪的难点问题之一,迄今为止,有关学者研究了多种定量确定小波去噪分解尺度的方法[4-8],大致可分为基于信号特征和基于噪声特征两类方法。目前,还缺乏系统性地评价这些方法应用的优缺点。本文重点结合已有的4种小波去噪分解尺度确定方法,通过仿真实验和实测数据的对比分析,着重探讨各种方法在信号处理中确定最佳分解尺度的适应性,为定量确定小波去噪分解尺度提供参考依据。
1 小波去噪分解尺度确定方法 1.1 基于均方根误差变化率的方法基于均方根误差变化率的分解尺度确定方法,记小波m级分解与重构信号的均方根误差为[5]:
| $\text{RMSE}(m)=\sqrt{\sum\limits_{i=1}^{n}{{{(x\left( i \right)-{{{\hat{x}}}_{m}}\left( i \right))}^{2}}}/n}$ | (1) |
式中,
| ${{r}_{m}}={\text{RMSE}(m+1)}/{\text{RMSE}(m)}\;, m=2, 3, 4, \cdots $ | (2) |
一般地,总有rm>1,且随着尺度的增大收敛于1,通常取rm≤1.1时,认为噪声基本消除,这时取分解尺度m或m+1为最佳分解尺度。
1.2 基于总体评价指标的综合法为了全面反映去噪效果,利用均方根误差变化量v(m)、互相关系数ρ(m)、信噪比SNR (m) 以及平滑度r(m)4个指标构造统计量为[6]:
| $H(m)={{P}_{v}}(m)+{{P}_{\rho }}(m)+{{P}_{\text{SNR}}}(m)+{{P}_{r}}(m)$ | (3) |
式中,相邻两级的均方根误差变化量为:
| $v(m)=\text{RMS}(m+1)-\text{RMS}(m)$ | (4) |
互相关系数为:
| $\rho (m)=\operatorname{cov}({{\hat{x}}_{m}}(i), x(i))/({{\sigma }_{x}}\cdot {{\sigma }_{{{{\hat{x}}}_{m}}}})$ | (5) |
信噪比为:
| $\text{SNR}(m)=10\lg (\sum\limits_{i=1}^{n}{x{{(i)}^{2}}}/\sum\limits_{i=1}^{n}{{{(x(i)-{{{\hat{x}}}_{m}}(i))}^{2}})}$ | (6) |
平滑度为:
| $\begin{align} &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ r(m)= \\ &\sum\limits_{i=1}^{n-1}{({{{\hat{x}}}_{m}}\left( i+1 \right)-{{{\hat{x}}}_{m}}\left( i \right)}{{)}^{2}}/\sum\limits_{i=1}^{n-1}{(x\left( i+1 \right)-x\left( i \right)}{{)}^{2}} \\ \end{align}$ | (7) |
分别将v(m) 和r(m) 依式 (8) 归一化到[0,1],ρ(m) 和SNR (m) 依式 (9) 归一化到[0,1],使得最优的评价指标等于1,最差的评价指标等于0,得到归一化后的各项指标依次为Pv(m)、Pρ(m)、PSNR(m) 和Pr(m)。
| ${{P}_{i}}=({{h}_{\max }}-{{h}_{i}})/({{h}_{\max }}-{{h}_{\min }})$ | (8) |
| ${{P}_{i}}=({{h}_{i}}-{{h}_{\min }})/({{h}_{\max }}-{{h}_{\min }})$ | (9) |
基于总体指标的综合评价法,总体评价指标H(m) 越大,则去噪效果越好。因此当H(m) 取最大值时,对应的m为最佳分解尺度。
1.3 多指标融合法基于多指标融合的尺度确定法,其基本思想是借助具有代表性的相邻分解尺度均方根误差、信噪比、平滑度指标的变化反映去噪效果[7]。构造由相邻分解尺度的均方根误差、信噪比、平滑度变化组成的统计量vrm (m)、vsnr (m)、vr (m) 为:
| $\left\{ \begin{align} &\text{vrm}(m)=\text{RMSE}(m+1)-\text{RMSE}(m) \\ &\text{vsnr}(m)=|\text{SNR}(m+1)-\text{SNR}(m)| \\ &\text{vr}(m)=|r(m+1)-r(m)| \\ \end{align} \right.$ | (10) |
将以上3个指标的数据依式 (9) 进行归一化处理,将归一化的各指标进行融合处理,构造出一个新的统计量为:
| $F(m)={{\omega }_{\text{vrm}}}{{P}_{\text{vrm}}}(m)+{{\omega }_{\text{vsnr}}}{{P}_{\text{vsnr}}}(m)+{{\omega }_{\text{vr}}}{{P}_{\text{vr}}}(m)$ | (11) |
式中,Pvrm(m)、Pvsnr(m)、Pvr(m) 分别为均方根误差变化量、信噪比变化量、平滑度变化量归一化后的值;ωvrm、ωvsnr、ωvr分别为均方根误差变化量、信噪比变化量、平滑度变化量的权系数。这里采用熵值法确定权系数的值[9],随着分解尺度的增加,各变量表现出一定的收敛性,因此可根据融合指标收敛处的拐点所处位置判定最佳分解尺度。
1.4 复合评价指标法复合评价指标法是在传统的评价指标中选取一对呈负相关且具有相同的单调性的评价指标 (均方根误差、平滑度) 构建一个新的统计量[8]为:
| $T(m)={{w}_{\text{RMSE}}}{{P}_{\text{RMSE}}}+{{w}_{r}}{{P}_{r}}$ | (12) |
式中,PRMSE、Pr分别为均方根误差、平滑度依照式 (10) 中第一式归一化处理后的结果;wRMSE、wr分别为均方根误差、平滑度所赋的权系数,这里采用变异系数定权的方法确定权系数[10]。在数据处理过程中,选定小波分解范围,并计算各分解尺度下统计量T(m) 的值,当T(m) 达到最小值时,此时的m为最佳分解尺度。
2 仿真实验 2.1 模拟变形监测数据为了能够准确获得信号在不同分解尺度下的去噪效果,需要一组真值已知的数据进行分析。现模拟一组长度为1 024、由3个振幅频率不同的周期项和一个趋势项组成的变形监测数据S,如图 1所示,其表达式为:
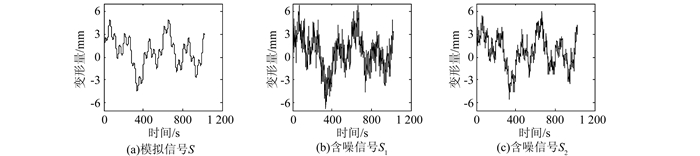 |
| 图 1 模拟变形监测数据 Figure 1 Simulated Deformation Monitoring Data |
| $ \begin{align} &S=3\sin (2\text{ }\!\!\pi\!\!\text{ }t/500){{e}^{-t/1000}}+2\sin (2\text{ }\!\!\pi\!\!\text{ }t/200)+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \sin (2\text{ }\!\!\pi\!\!\text{ }t/50)+t/1\ 000 \\ \end{align} $ | (13) |
为了对比分析以上4种方法在不同噪声强度影响下确定小波去噪分解尺度的能力,在模拟数据S中分别加入信噪比为7 dB (如图 1(a)所示) 和12 dB (如图 1(b)所示) 两种不同程度的噪声,得到含噪信号S1、S2。这里选取db4小波基函数采用最优预测变量阈值准则及软阈值函数分别对S1、S2在分解尺度2~8范围做小波去噪处理。
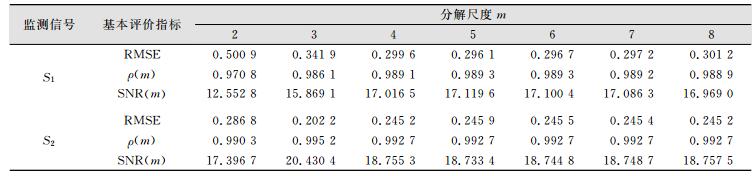
2.2 模拟数据分析由于模拟变形监测信号S的真值是已知的,因此这里可利用重构信号与模拟信号真值间的均方根误差、互相关系数、信噪比来准确判定小波去噪的最佳分解尺度。对信号S1、S2做去噪处理,计算各评价指标如表 1所示。由表 1可知,信号S1、S2分别在分解尺度m为5、3时,均方根误差最小,互相关系数、信噪比最大,因此,可确定模拟变形监测信号S1、S2小波分解的最佳分解尺度m分别为5、3。
| 表 1 模拟变形监测信号S1和S2去噪后质量评价指标 Table 1 De-Noised Quality Evaluation Index of Simulation Signal S1 and S2 |
 |
根据前述4种方法分别对模拟信号S1、S2在不同分解尺度上小波去噪处理后的评价指标值:①依据基于均方根误差变化率的方法在rm≤1.1时,取得最佳分解尺度;②基于总体评价指标的综合法在H(m) 最大时,取得最佳分解尺度;③多指标融合法在指标变化发生拐点时,取得最佳分解尺度;④复合评价指标法在T(m) 最小时,取得最佳分解尺度,判定出4种方法确定的分解尺度,如图 2所示,图中,“▼”和“○”分别为信号S1和S2在不同分解尺度处理后得到的相应评价指标值。
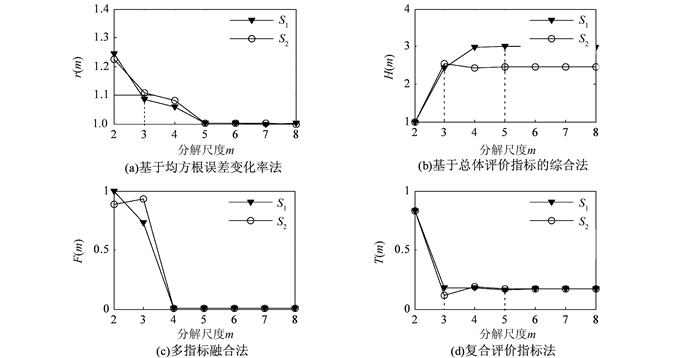 |
| 图 2 4种方法对分解尺度的确定结果 Figure 2 Results of Four Methods Determined Decomposition Scale |
由图 2可以发现,随着分解尺度的增大,对于噪声强度较高的S1信号,基于均方根误差变化率的方法在分解尺度m=3时,rm≤1.1,由此确定的最佳分解尺度为3,与实际情况不符;多指标融合法在分解尺度m=4时有明显拐点,最佳分解尺度为4,也不符合实际情况;基于总体评价指标的综合法和复合评价指标法在m=5时分别有H(m) 达到最大和T(m) 达到最小,均正确判断出小波去噪的最佳分解尺度。
类似地,对于包含噪声较弱的S2信号,基于均方根误差变化率的方法、基于总体评价指标的综合法和复合评价指标法,在m=3时均取得最佳分解尺度,与实际情况相符;而多指标融合法在m=4时有明显拐点,与实际情况不符,不能准确确定小波去噪的最佳分解尺度。
综上分析,4种方法的本质是用均方根误差、互相关系数、信噪比、平滑度中的部分或全部评价指标构造一个统计量,使其能够反映去噪结果与分解尺度的关系。基于均方根误差变化率的方法,因其仅依靠均方根误差变化率单一指标判断,不能全面反映信号特征,其在处理噪声较低的信号时能取得良好的效果;总体评价指标的综合法选取了误差变化量、相关系数、信噪比以及光滑度4种指标对去噪后的信号进行评价,以期全面反映信号的质量,结果表明,它能较好地确定小波去噪的最佳分解尺度,且受噪声影响较小;多指标融合法和复合评价方法是在总体评价指标的综合法基础上进行的改进,针对评价指标随分解尺度增大所表现出的单调性、收敛性,选取有代表性的评价指标分别构造统计量F(m)、T(m),并对各个评价指标的系数做定权处理,结果表明,多指标融合法能确定分解尺度的大致位置,而复合评价方法能较好地确定小波分解的最佳分解尺度。
3 工程实例在工程应用中数据去噪对后续数据预测有重要的意义。4种方法在变形监测数据去噪处理的应用如下。
这里选取的数据序列为某一地铁变形监测点x方向上的222期累计变形量监测数据。由于监测数据的变形真值未知,因此不能通过均方根误差、信噪比、平滑度等评价指标准确判断最佳分解尺度。为方便比较,选择具有良好正交性、紧支性的db4小波基函数,采用最优预测变量阈值准则及软阈值函数对监测数据做分解尺度2~8的去噪处理,分别计算出4种方法的统计评价指标rm、H(m)、F(m)、T(m),结果如表 2所示。
| 表 2 不同尺度小波去噪后评价指标值 Table 2 Evaluation Values of Different Scale Wavelet De-Noising |
 |
由小波去噪分解尺度判定条件对比发现,基于均方根误差变化率的方法、基于总体评价指标的综合法在分解尺度m=3时取得最佳分解尺度;而多指标融合法、复合评价指标法在m=4时取得最佳分解尺度,表明其可能的最佳分解尺度分别为3、4。实测数据及其分解尺度为3、4时的去噪结果如图 3所示。
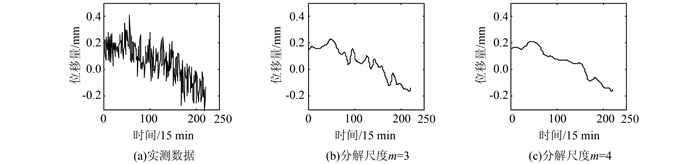 |
| 图 3 实测数据及不同分解尺度小波去噪后的结果 Figure 3 Measured Data and the Results with Different Decomposition Scales |
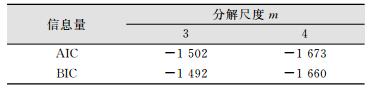
由图 3可见,小波分析取分解尺度为3、4时,都能够较好地消弱实测数据的噪声,但无法直观判断最佳分解尺度。而最小信息量准则 (Akaike information criterion, AIC)、贝叶斯信息量准则 (Bayesian information criterion, BIC) 的方法[11]在确定包含白噪声为主信号的小波分解尺度时具有很好的效果,又能较大程度地保留信号的细节部分。因此,这里借助这两种方法对实测数据进行处理,进一步确定小波分解尺度。计算分解尺度m=3、m=4时的AIC、BIC值,其结果如表 3所示,并对实测数据和去噪数据作频谱分析,如图 4所示。
| 表 3 不同尺度小波去噪后的信息准则计算值 Table 3 Calculated Values of Information Criterion with Different Scale Wavelet De-Noising |
 |
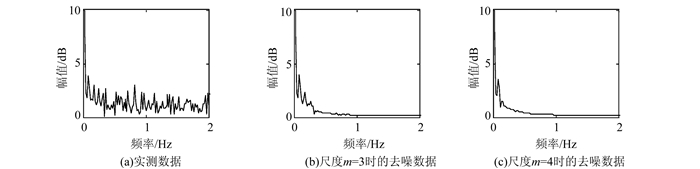 |
| 图 4 实测数据及不同分解尺度去噪后的数据频谱 Figure 4 Measured Data and Frequency Spectrum with Different Scales De-Noising |
由表4可见,分解尺度m=4时的AIC、BIC同时达到最小,表明分解尺度m=4时信息量达到最小。由图 4可以看出,分解尺度m=4时去噪后的信号一方面较多地剔除了高频成分,而另一方面又保留了信号的细节部分,取得了较好的去噪效果。
4 结束语本文介绍了小波去噪的4种分解尺度确定方法,并对模拟数据和实测数据进行处理,给出了各种方法在变形监测数据去噪中确定最佳分解尺度的应用效果。对比分析表明:①基于均方根误差变化率的方法计算简单,但对噪声比较敏感,适合处理噪声较少的信号;②多指标融合法在确定小波分解尺度有一定的偏差,但对噪声的抵抗性较好;③基于总体评价指标的综合法和复合评价指标法能够准确定位出最佳小波去噪分解尺度,且不受噪声污染水平不同的影响。此外,在实际数据处理中,由于无法知道信号的噪声强度等先验信息,为了提高分解尺度确定的可靠性,应至少选择两种方法对实测数据进行处理,同时比较分析它们去噪结果的时频特征等信息,以最终确定分解尺度,保证数据去噪处理中消除噪声的同时又保留变形特征。
| [1] | 黄声享, 刘经南. GPS变形监测系统中消除噪声的一种有效方法[J]. 测绘学报, 2002, 31(2): 104–107 |
| [2] | 黄声享, 刘经南, 柳响林. 小波分析在高层建筑动态监测中的应用[J]. 测绘学报, 2003, 32(2): 153–157 |
| [3] | 赵卿, 黄声享. 基于最小信息量准则的小波变换确定变形监测精度[J]. 测绘信息与工程, 2009, 34(5): 46–47 |
| [4] | 王维, 张英堂, 任国全. 小波阈值降噪算法中最优分解层次的自适应确定及仿真[J]. 仪器仪表学报, 2009, 30(3): 526–530 |
| [5] |
文鸿雁. 基于小波理论的变形分析模型研究[D]. 武汉: 武汉大学, 2004 |
| [6] | 李宗春, 邓勇, 张冠宇, 等. 变形测量异常数据处理中小波变换最佳尺度的确定[J]. 武汉大学学报·信息科学版, 2011, 36(3): 285–288 |
| [7] | 陶珂, 朱建军. 多指标融合的小波去噪最佳分解尺度选择方法[J]. 测绘学报, 2012, 41(5): 749–755 |
| [8] | 朱建军, 章浙涛, 匡翠林, 等. 一种可靠的小波去噪质量评价指标[J]. 武汉大学学报·信息科学版, 2015, 40(5): 688–694 |
| [9] | 解传银. 基于权重模型的滑坡灾害敏感性评价[J]. 中南大学学报 (自然科学版), 2011, 42(6): 1 772–1 779 |
| [10] | 邓敏, 吴光强. 基于变异系数的小波降噪综合评价法[J]. 机电一体化, 2016, 3(6): 30–35 |
| [11] | 向东, 贡建兵. 变形序列小波去噪最佳分解尺度量化指标的确定[J]. 武汉大学学报·信息科学版, 2014, 39(4): 468–470 |
 2017, Vol. 42
2017, Vol. 42

