| WiFi室内距离交会定位位置的迭代解法 |
近年来,室内定位技术发展迅速,如无线保真(wireless fidelity,WiFi)、红外线、超带宽无线电、射频标签、蓝牙、LED可见光、伪卫星技术等[1]。在上述室内定位技术中,由于WiFi无线定位不需要添加额外的硬件设备, 并且定位成本低廉,已经成为目前室内定位的主要技术方法[2]。以接收信号强度(received signal strength indication, RSSI)为观测值,一般有以下两类定位方法:① 利用信号传输模型将RSSI转化为距离,进行距离交会;② 离线阶段建立RSSI与采样位置的对应关系,在线阶段通过位置指纹算法匹配出与实时信号强度最佳匹配的位置。这两种方法都对RSSI的稳定性要求较高,在RSSI预处理阶段,需要剔除部分RSSI值的异常数据,并通过高斯滤波减小RSSI值的波动幅度,提高RSSI信号的质量[3]。
在距离定位模型中,考虑到近似坐标误差过大导致定位模型的线性化误差不可忽略,本文采用迭代方法进行室内定位解算,并用实测数据对定位效果进行了验证。
1 WiFi接收信号强度测距模型常用的无线信号传播模型有自由空间传播模型、对数距离路径损耗模型、对数-常态分布模型等[4]。自由空间模型是发射机和接收机之间没有障碍物,且在视距(line-of-sight, LOS)环境下的接收信号强度模型[5]。离辐射源距离为d处的接收功率Pr(d)用Friis公式表示为[6]:
| $ {P_r}\left( d \right) = \frac{{{P_t}{G_t}{G_r}{\lambda ^2}}}{{{{\left( {4{\rm{\pi }}} \right)}^2}{d^2}L}} $ | (1) |
式中,Pt为发射天线的辐射功率; Gt为发射天线的增益; Gr为接收天线的增益; λ是电波的波长; L是系统硬件的损耗,与传播环境无关。若系统硬件没有损耗,则L=1, 且发射端和接收端的天线增益相同,由式(1) 可导得对数路径损耗模型[7]为:
| $ R\left( d \right) = {R_0}\left( {{d_0}} \right) - 10n\lg \left( {d/{d_0}} \right) $ | (2) |
式中,d为接收端与发射端之间的距离;R(d)和R0(d0)分别为离发射端距离为d和d0处的接收信号强度;n代表信号随距离损耗的路径损耗因子。取d0=1 m作为参考距离,根据若干个坐标已知的观测点至发射端的距离di,采用最小二乘法求得式(2) 中的参数R0(d0)和n,建立当前室内环境的接收信号强度与距离的关系模型[8]。
2 WiFi室内距离交会定位位置解算方法 2.1 最小二乘解法若有n(n > 3) 个观测点,其坐标为(xi, yi), i=1, 2, …, n,待定点坐标为(x, y),观测点至待定点的距离为di,则可形成n个观测方程为[9]:
| $ \left\{ {\begin{array}{*{20}{c}} {{{\left( {{x_1} - x} \right)}^2} + {{\left( {{y_1} - y} \right)}^2} = {d_1}^2}\\ {\begin{array}{*{20}{c}} {{{\left( {{x_2} - x} \right)}^2} + {{\left( {{y_2} - y} \right)}^2} = {d_2}^2}\\ \vdots \end{array}}\\ {{{\left( {{x_n} - x} \right)}^2} + {{\left( {{y_n} - y} \right)}^2} = {d_n}^2} \end{array}} \right. $ | (3) |
观测方程(3) 是n个关于x、y的非线性方程,根据两个交会角度较好的距离求得待定点的近似值(x0, y0),代入式(3) 线性化后,其观测方程用矩阵和向量可以表示为:
| $ y = A\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{e}} $ | (4) |
式中,y为线性化后的观测向量;x=(δx,δy)T为待定点坐标改正数;A为常系数矩阵;e为观测误差向量。利用最小二乘法求得待定点的坐标及其精度[10],其坐标改正数为:
| $ \mathit{\boldsymbol{x}} = {\left( {{{\bf{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}^{\rm{T}}}}\mathit{\boldsymbol{Py}} $ | (5) |
式中,P为观测权阵,与待定点到观测点距离的平方成反比。平差后的坐标为:xL=x0+δx,yL=y0+δy,其精度为:
由于WiFi距离观测误差相对于距离值比较大,因此近似值(x0, y0)的误差也比较大,导致设计矩阵A也存在较大的误差,则最小二乘法求得的待定点坐标(xL, yL)必定受设计矩阵A的误差的影响。为了削弱A的误差的影响,以(xL, yL)为初值进行高斯-牛顿迭代法计算。第k+1次迭代计算时,用第k次迭代求得的坐标(x(k), y(k))计算系数矩阵A(k)和观测常数项y(k)。则k+1次迭代计算的观测方程为:
| $ {\mathit{\boldsymbol{y}}_{\left( k \right)}} = {\mathit{\boldsymbol{A}}_{\left( k \right)}}{\mathit{\boldsymbol{x}}_{\left( k \right)}} + \mathit{\boldsymbol{e}} $ | (6) |
式中,x(k)=(δx(k), δy(k));矩阵A(k)的第i行可表示为
| $ {\mathit{\boldsymbol{x}}_{\left( {k + 1} \right)}} = {\left( {{\mathit{\boldsymbol{A}}_{\left( k \right)}}^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{A}}_{\left( k \right)}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}_{\left( k \right)}}^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{y}}_{\left( k \right)}} $ | (7) |
则第k+1次迭代坐标为:x(k+1)=x(k)+δxk+1,y(k+1)=y(k)+δy(k+1)。若小于给定迭代终止的门限,则终止迭代。
3 实验及结果分析 3.1 WiFi信号传播特性分析为了探究接收信号强度随时间变化的关系[11], 利用安卓手机应用程序编程接口(API)中提供的方法,在布设有WiFi节点的同济大学信息馆底楼,采用D-Link_DIR-859和TP-Link_0F784E路由器以及HTC D861t手机进行RSSI测试。测试时间在下午1:00左右,人员干扰较少。每更新800次,RSSI数据自动将采集结果保存并导出。图 1(a)为距TP-Link_0F784E路由器1.2 m处(均值为-67.687 dBm,标准差为2.251 dBm)800个采样值的处理结果;图 1(b)为距D-Link_DIR-859路由器7.2 m处(均值为-63.108 dBm,标准差为1.032 dBm)800个采样值的处理结果。
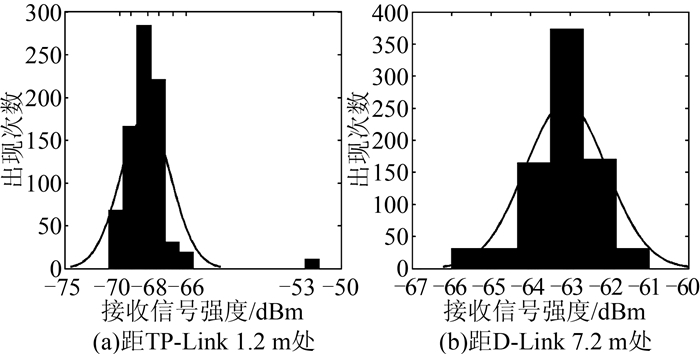 |
| 图 1 RSSI分布直方图 Figure 1 RSSI Distribution Histogram |
实验结果表明,不同型号路由器用相同手机测得的接收信号强度随距离衰减程度不同;同一个路由器,在某个固定位置,长时间对接收信号强度进行采样,其数值在一定范围内波动,且符合类正态分布[12]。剔除偏离平均值较大的值(如图 1(a)中的-53 dBm)后,求取信号强度的平均值作为该点的WiFi信号特征。
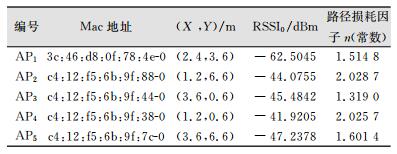
3.2 WiFi室内距离交会定位实验分析在同济大学信息馆的底楼进行了基于距离模型的定位实验。本定位实验场地面积为4.8 m×7.2 m,在室内布设了5个AP,按照实测数据拟合了各个AP当前室内环境的对数路径损耗模型的参数,每个AP的Mac地址、坐标位置、1 m处的RSSI值(RSSI0)和路径损耗因子n(n为常数)如表 1所示。
| 表 1 五个定位AP相关信息 Table 1 Information of Five Positioning APs |
 |
本文选取23个点进行WiFi定位,分别采用最小二乘法与基于高斯-牛顿迭代法进行解算,当改正数(δx(k), δy(k))均小于0.01 m时停止迭代。这些点位的最小二乘法坐标和高斯-牛顿迭代法解算结果如表 2所示,其中ΔX、ΔY表示解算结果与已知坐标的差值。同时,为便于分析比较,表 2还给出了改进加权K近邻(weighted K-nearest neighbor, WKNN)算法[13]的指纹匹配定位结果。X和Y坐标的中误差计算公式如下:
| $ {M_X} = \sqrt {\frac{{\mathop \sum \nolimits_{j = 1}^N \Delta X_j^2}}{N}}, \;\;{M_Y} = \sqrt {\frac{{\mathop \sum \nolimits_{j = 1}^N \Delta Y_j^2}}{N}} $ | (8) |
| 表 2 普通最小二乘法、高斯-牛顿迭代法与位置指纹算法解算结果对比/m Table 2 Results Comparison of Three Algorithms/m |
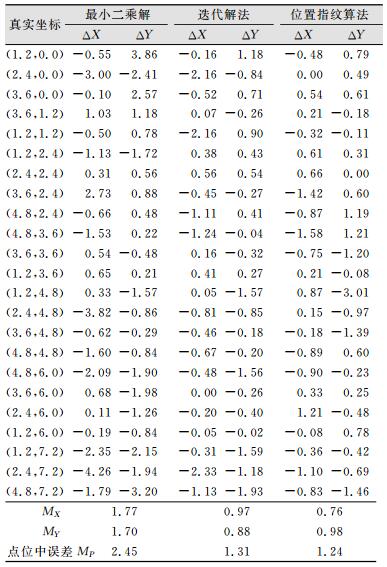 |
点位中误差
由表 2可以看出,采用高斯-牛顿迭代法解算的待定点坐标与已知坐标的差值比最小二乘解的结果明显要小,其精度提高了1.87倍;利用WKNN位置指纹算法求得的定位精度要高于高斯-牛顿迭代法,其原因可能因为本文采用距离平方倒数来定权。如果建立WiFi测距信号严格的随机模型,将有望进一步提高迭代解的精度。
4 结束语本文利用高斯-牛顿迭代解法进行WiFi测距信号的室内定位,给出了相应的迭代解算公式。利用同济大学信息馆底楼实验场地实际测试数据分析了WiFi信号的传播特性,求出了最优拟合当前室内环境的对数路径损耗模型的参数,建立了测距信号强度与距离的关系模型,并利用23个点的实测WiFi定位数据进行了分析。结果表明,迭代解法能削弱近似坐标误差过大对定位结果的影响。采用WKNN位置指纹算法的精度比迭代解法的精度更高,部分原因是迭代解法采用简单的距离平方倒数的定权模式。
| [1] | Geng Yuyang, Zhang Shuhang, Wu Hangbin, et al. Improved Indoor Positioning System Based on WiFi RSSI: Design and Deployment[C]// Liu Chun. Principal and Application Progress in Location-Based Services.USA:Springer, 2014 |
| [2] | 李桢, 黄劲松. 基于RSSI抗差滤波的WiFi定位[J]. 武汉大学学报·信息科学版, 2016, 41(3): 361–366 |
| [3] |
陈姣. 基于RSSI测距的WiFi室内定位技术研究[D]. 绵阳: 西南科技大学, 2012 |
| [4] |
鲁文强. 室内无线指纹的多模型匹配方法研究[D]. 成都: 电子科技大学, 2013 |
| [5] | 田孝华, 周义建. 无线电定位理论与技术[M]. 北京: 国防工业出版社, 1993 |
| [6] | 陈岭, 许晓龙, 杨清, 等. 基于三次样条插值的无线信号强度衰减模型[J]. 浙江大学学报, 2011, 45(9): 1 521–1 538 |
| [7] |
张颖. 无线定位优化算法的研究[D]. 西安: 西安邮电大学, 2011 |
| [8] | 毕京学, 甄杰, 郭英. 室内定位无线接收信号强度测距模型的研究[J]. 导航定位学报, 2014, 2(4): 8–10 |
| [9] | 刘少飞, 赵清华, 王华奎. 基于平均跳距估计和位置修正的DV-Hop定位算法[J]. 传感技术学报, 2009, 22(8): 1154–1 158 |
| [10] | 程秀芝, 朱达荣, 张申, 等. 基于RSSI差分校正的最小二乘-拟牛顿定位算法[J]. 传感技术学报, 2014, 27(1): 123–127 |
| [11] | 崔惠媚, 王小伟, 王伟, 等. 基于WiFi的室内定位系统[J]. 微型机与应用, 2014, 33(23): 58–60 DOI: 10.3969/j.issn.1674-7720.2014.23.030 |
| [12] |
雷家毅. Android平台基于WiFi的定位算法与系统设计[D]. 上海: 华东理工大学, 2012 |
| [13] | 薛卫星, 邱卫宁, 花向红, 等. RSSI信号特征值对WiFi室内定位精度的影响分析[J]. 测绘地理信息, 2016, 41(4): 23–26 |
 2017, Vol. 42
2017, Vol. 42

