| 联合RTK和支距法测定建筑物角点的方法及应用 |
基于实时动态(real-time kinematic, RTK)作业模式下的GPS测量定位技术,以实时定位、施测灵活、全天候作业和高效率等优点[1, 2]深受广大测量工作者的喜爱,进而被广泛用于数字地形图测绘[3]、地籍测量[4-6]、工程设计放样[7]和国土资源调查[8, 9]等诸多领域。然而,利用RTK定位技术测量形状为直角形的建筑物角点时却存在以下两个突出的问题:①因为建筑物自身高度的遮挡使RTK接收机天线不能同时接收到4颗(或者4颗以上)GPS卫星的信号,导致无法实时的测量和计算出建筑物角点的坐标,或者建筑物角点的解算结果精度很差,远不能满足相应的规范或工程建设的需要;②因为RTK接收机天线自身具有一定的几何尺寸,从而使RTK接收机无法与建筑物角点完全贴近,导致测定的结果产生较大的偏差。本文研究了基于支距法的建筑物角点测量方法,支距分为单边支距和双边支距,双边支距又分为等距离双边支距和不等距离双边支距。
1 基于支距法的建筑物角点测定方法由于建筑物自身高度的遮挡以及RTK接收机几何形状的影响,导致无法利用RTK直接测量建筑物的角点。支距法建筑物角点测量,即是在建筑物角点为直角的情况下将角点向外延伸(延伸的长度由建筑物的高低及周边环境等因素决定),利用RTK定位技术测定角点平面坐标的一种测量方法。由于延伸后得到的点位和建筑物之间已经有一段距离,因此将RTK接收机安置在该点位不会受到RTK接收机自身几何形状和建筑物高度遮挡的影响。
1.1 基于单边支距法测定角点的原理及其计算公式单边支距法建筑物角点测量如图 1所示,首先将一条较长的直杆平铺在地面上,并使直杆的底端紧贴墙角Q点,然后将RTK接收机天线杆分别安置在直杆的A、B两点上,测定A、B两点的平面坐标为(XA, YA)和(XB, YB),量取BQ之间的距离为SBQ。
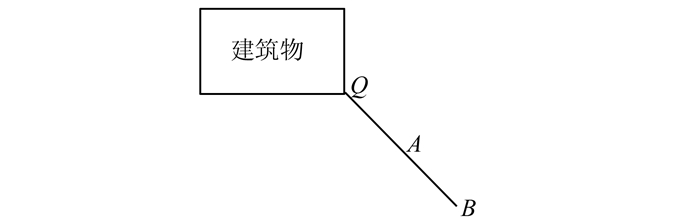 |
| 图 1 单边支距法角点测量原理图 Figure 1 Unilateral Margin Method of Measuring Point of Principle Diagram |
通过RTK测定得到的A、B两点的平面坐标可计算得到直线BA的坐标方位角为:
| $ {\alpha _{BA}} = \frac{{{X_A} - {X_B}}}{{{Y_A} - {Y_B}}} $ | (1) |
则可根据B点的坐标(xB, yB)和量取得到的距离SBQ,计算建筑物角点Q的坐标为:
| $ \left\{ \begin{array}{l} {X_Q} = {X_B} + {S_{BQ}} \cdot \cos {\alpha _{BA}}\\ \;{Y_Q}\; = \;\;{Y_B}\; + \;{S_{BQ}} \cdot \sin {\alpha _{BA}} \end{array} \right. $ | (2) |
如图 2所示,双边支距法建筑物角点测量,是将一条较长的直杆分别沿着建筑物角点Q的两侧墙面外伸出点A和B,必要时量取AQ或BQ的距离,然后将RTK接收机天线杆分别安置在A、B两点测定其平面坐标,进而计算得到建筑物角点平面位置的测量方法。
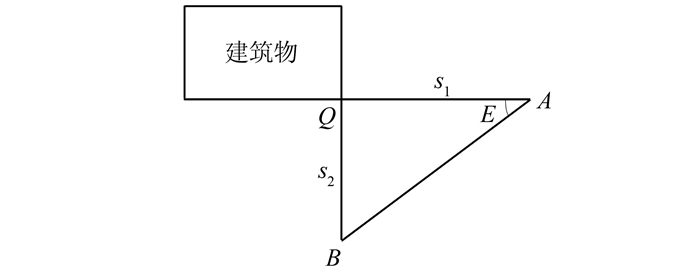 |
| 图 2 双边支距法角点测量原理图 Figure 2 Bilateral Distance Measurement Method of Measuring Point Diagram |
1.2.1 等距离双边支距法
当建筑物及其周边环境允许时,保持延伸点A、B与建筑物角点距离相等的方法称为等距离支距法,该方法只需利用RTK测定A、B两点的平面坐标、不需测量延伸点至角点的距离(可将直杆底部紧贴角点的一侧墙面放样延伸点A,再将直杆底部紧贴角点的另一侧墙面放样延伸至点B,进而实现SAQ=SBQ,且达到无需测量延伸点至角点距离的目的),建筑物角点坐标的计算公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{X_Q} = {X_0} - \frac{{{S_{AB}}}}{2} \times \sin {\alpha _{BA}}}\\ {\;{Y_Q}\; = \;\;{Y_0}\; + \;\frac{{{S_{AB}}}}{2} \times \cos {\alpha _{BA}}} \end{array}} \right. $ | (3) |
式中,
当建筑物角点周边有障碍物阻碍测量工作者进行支距工作时,会导致延伸点A、B至建筑物角点的距离不相等,则应严格测量其中一条支距的长度,然后通过式(4)计算建筑物角点的坐标:
| $ \left\{ {\begin{array}{*{20}{l}} {{X_Q} = {X_0} - \frac{{{S_{AB}}}}{2} \times \cos ({\alpha _{AB}} + 2E \pm {{180}^\circ })}\\ {\;{Y_Q}\; = \;\;{Y_0}\; + \;\frac{{{S_{AB}}}}{2} \times \sin ({\alpha _{AB}} + 2E \pm {{180}^\circ })} \end{array}} \right. $ | (4) |
式中,
在利用式(4)计算建筑物墙角点的坐标时,当αAB在第一和第四象限时,180°前应取“+”号;当αAB在第二和第三象限时,180°前应取“-”号(在这里应注意测量坐标系的象限是按照顺时针次序排列的);当αAB=270°或αAB=90°时,180°前取“+”号或取“-”号都可以。
2 实例计算与精度分析利用RTK技术通过支距法测定建筑物角点具有以下的优点:
1) 利用RTK通过支距法测定建筑物角点时,RTK接收机天线不受建筑物的遮挡,能够同时接收到4颗(4颗以上)GPS卫星的信号,进而可以获得点位的固定解。此外,支距法角点测量还能有效避免RTK接收机天线的几何形状对测定坐标产生偏差的影响;
2) 等距离双边支距法只需测定延伸点的平面坐标、不需测量延伸点与角点之间的距离,有效的提高了建筑物角点坐标的计算精度;
3) 在实际测量作业中,当需要测定矩形建筑物的4个角点坐标时,则只需测量位于对角线上的两个角点的平面坐标,然后量取矩形建筑物的长或宽,再利用不等距离双边支距法的原理,通过式(4)计算其他两个角点的平面坐标;
4) 测量人员在测定建筑物角点时避免了全站仪的使用,可以直接通过RTK间接测定建筑物墙角点的平面坐标,这样就大幅度提高了野外测量的效率,同样也使测量的人力、物力、财力大大减少。
为了对支距法建筑物角点测量方法的可行性及其计算公式的正确性进行验证,笔者在河南测绘职业学院校园内进行了实际的测量实验。如图 3所示,T01、T02和T03是利用GPS与郑州城市坐标系已知点坐标进行联测得到的C级控制点,笔者在这些控制点上安置Leica TM30全站仪(标称精度:0.5″, 1 mm+1×10-6),采用三维坐标法[10]测量控制点周边建筑物的墙角点(1~10)平面坐标。考虑到墙角点不易架设棱镜,因此在这些墙角点处粘贴反光标,应用Leica TM30具有的免棱镜测量功能测量这些墙角点的坐标。由于测量仪器精度高、测量手段严密,因此将测量结果作为这些墙角点平面坐标的真实值。
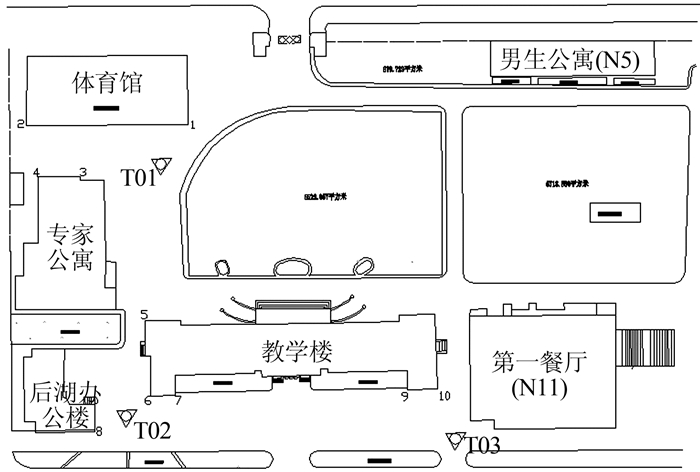 |
| 图 3 测量实验示意图 Figure 3 Measurement Experiment Diagram |
分别在控制点T01和T02处设立基准站,仪器使用型号为Leica GPS1200接收机,按照本文所述方法,依次使用单边支距法、不等距离双边支距法和等距离双边支距法测定并改算墙角点1~10的平面坐标。以Leica TM30测定的结果作为墙角点平面坐标的最或是值,分别将3种方法的测定结果与其做差,然后根据
| 表 1 三种方法测定建筑物角点平面位置的点位偏差/cm Table 1 Three Methods to Determine the Position of the Corner Point of the Building Site Deviation/cm |
 |
分析表 1中的数据可知,三种支距方法采集和改算得到的10个墙角点的点位偏差都非常小,最大的点位偏差为3.1 cm,最小的点位偏差为1.4 cm。单边支距法和不等距离双边支距法测定墙角点的点位偏差相互之间并无太大差别,而等距离双边支距法的测定精度有显著提高,其原因是无需测量支距的长度。因此,在测量环境允许的情况下,建议采用等距离双边支距法测定建筑物墙角点的坐标。
3 结束语基于支距法利用RTK定位技术测定建筑物墙角点的方法在理论上严密、计算公式简单,通过在河南测绘职业学院校内进行的精度分析,表明其测量精度完全满足大比例尺地形图测绘和地籍测量的需要;通过在河南省郑州市地籍调查中的实际应用表明该方法实际操作方便、内业工作量小,在测绘生产中是可行的。
| [1] |
黄声享, 郭英起, 易庆林. GPS在测量工程中的应用[M]. 北京: 测绘出版社, 2007.
|
| [2] |
谭先科, 黄劲松. 网络RTK模糊度解算与误差项提取方法研究[J]. 测绘地理信息, 2016, 41(6): 58-61. |
| [3] |
王杰. GPS RTK在数字地形图测绘中的应用[J]. 勘察科学技术, 2011(1): 47-48. DOI:10.3969/j.issn.1001-3946.2011.01.013 |
| [4] |
任志刚. CORS技术在城镇地籍测量中应用实例[J]. 现代测绘, 2011(2): 32-34. DOI:10.3969/j.issn.1672-4097.2011.02.010 |
| [5] |
喻华. GPS RTK技术在地籍测量中的应用[J]. 测绘通报, 2007(7): 51-52. DOI:10.3969/j.issn.0494-0911.2007.07.017 |
| [6] |
陈鸿志, 许承权, 周庆俊. 莆田市城镇地籍管理信息系统的开发及应用[J]. 测绘地理信息, 2014, 39(2): 39-41. |
| [7] |
梁振华, 孟凡超. 南方单基站CORS技术在工程放样中的应用[J]. 全球定位系统, 2012(3): 53-55. DOI:10.3969/j.issn.1008-9268.2012.03.016 |
| [8] |
蔡建忠, 张志勇. 实时动态定位技术在土地勘测工作中的应用[J]. 测绘通报, 2003(5): 32-34. DOI:10.3969/j.issn.0494-0911.2003.05.010 |
| [9] |
董瑞伶, 宫辉力, 赵文吉, 等. 3S技术在国土资源大调查中的应用初探[J]. 首都师范大学学报(自然科学版), 2006, 24(1): 93-97. DOI:10.3969/j.issn.1004-9398.2006.01.021 |
| [10] |
毕继鑫, 田林亚, 张洋, 等. 基于PDA的空间圆形物体形态检测与分析系统的开发及应用[J]. 工程勘察, 2017, 45(9): 40-43. |
 2018, Vol. 43
2018, Vol. 43

