| GNSS单点解算用于组合导航性能分析 |
随着应用环境的日趋复杂,GNSS(global navigation satellite system)需要和其他多种导航系统结合起来,例如INS(inertial navigation system)来实现高可靠连续的定位于导航的需求[1]。GNSS信息和INS信息融合过程中,普遍采用标准卡尔曼滤波方法,该方法的前提要求是观测输入符合白噪声[2]。然而,将它们都当成白噪声会导致卡尔曼滤波器输出方差/协方差阵矩阵,即P阵,相对于现实误差水平过小[3]。
GNSS单点解算中常用的估计方法主要有最小二乘和卡尔曼滤波。最小二乘是最常用的估计理论,它通过最小化误差的平方和寻找数据的最佳函数匹配;卡尔曼滤波算法采用信号和噪声的状态空间模型,利用前一时刻地估计值和现时刻的观测值来更新对状态变量的估计,求出现实可的估计值状态估计是卡尔曼滤波的重要组成[4]。
组合导航领域对IMU(inertial measurement unit)误差建模较多,有基于传统高斯马尔科夫过程的建模方法[5],也有基于自回归(AR)模型的建模方法[6],但对GNSS定位误差噪声类型分析较薄弱。文献[7]基于时间序列对GPS误差进行了建模,但未对GPS误差类别进行说明与分析。文献[8]中利用Allan方差对3种GNSS定位模式下误差类别进行了识别,但未应用于组合导航中进行分析。
本文利用Allan方差识别基于最小二乘和卡尔曼滤波两种估计算法的GNSS单点解算位置误差大小和类别,并应用于GNSS/INS组合导航实际工作环境,通过实际性能来说明最小二乘算法下的GNSS单点解算结果是否适用GNSS/INS组合导航。
1 最优估计 1.1 最小二乘假设测量值x=[x1, x2, …, xk]T是n维常值向量, y=[y1, y2, …, yk]T; 向量y是x的线性组合,
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Hx}} + \mathit{\boldsymbol{\upsilon }} $ | (1) |
定义残差为
| $ \mathit{\boldsymbol{J}} = \varepsilon _{{y_1}}^2 + \cdots + \varepsilon _{{y_k}}^2 = \mathit{\boldsymbol{\varepsilon }}_y^{\rm{T}}{\mathit{\boldsymbol{\varepsilon }}_y} = {(\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{H\hat x}})^{\rm{T}}}(\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{H\hat x}}) $ |
最小二乘准则要求J最小,则J对
| $ \mathit{\boldsymbol{\hat x}} = {({\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}})^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{y}} $ | (2) |
卡尔曼滤波建立的系统方程和观测方程如下:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{F}}_{k + 1}} + {\mathit{\boldsymbol{G}}_{K - 1}}{\mathit{\boldsymbol{u}}_{k - 1}} + {\mathit{\boldsymbol{\omega }}_{k - 1}}}\\ {{\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{\upsilon }}_k}} \end{array} $ | (3) |
其中不同时刻的噪声项相互独立。ωk为系统噪声,υk为测量噪声。使
| $\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}} = {{\mathit{\boldsymbol{\hat x}}}^ - } + {\mathit{\boldsymbol{K}}_k}(\mathit{\boldsymbol{y}}{}_k - {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{\hat x}}_k^ - )}\\ {{\mathit{\boldsymbol{K}}_K} = \mathit{\boldsymbol{P}}_k^ + \mathit{\boldsymbol{H}}_k^{\rm{T}}\mathit{\boldsymbol{R}}_K^{ - 1}} \end{array} $ | (4) |
与最小二乘估计方法相比,卡尔曼滤波估计方法当前历元的状态估计与上一时刻的状态相关,故估计结果表现出一定的时间相关性。在大多数GNSS用户设备中,由于GNSS定位观测是非线性问题,载体的运动轨迹也具有非线性,大多采用扩展卡尔曼滤波算法[9]。
2 利用Allan方差分析GNSS单点定位误差 2.1 Allan方差Allan方差是在时域上对频率特性进行分析的一种方法,最早用于时钟频率稳定性的时域特征分析是IEEE公认的陀螺仪参数辨识的标准方法[10]。Allan方差分析已被广泛运用于随机过程的识别并成为其首选方法[11],例如量化噪声、白噪声、相关噪声、正弦噪声、随机游走和闪烁噪声。Allan方差基本解算流程[12]如下。
1) 假设N个连续采样点yi,i=1, 2,…,N,采样间隔为t0,数据采样时间为τ0。任意时间簇τ=(n-1)×t0(n<N/2), 按照时间簇τ的长度将yi分隔后成NC个数据块。
2) 计算每个时间簇τ对应数据块内的数据平均值yk(k=1, 2, 3, …, Nc),其计算公式可以表示为:
| $ {\bar y_k} = \frac{1}{n}\sum\limits_{i = k}^{k + n - 1} {{y_i}} $ | (5) |
3) 计算时间簇τ的Allan方差:
| $ {\sigma ^2}\left( \tau \right) = \frac{1}{{2({N_c} - 1)}}\sum\limits_{k = 1}^{{N_c} - 1} {({{\bar y}_{k + 1}} - {{\bar y}_k})} $ | (6) |
在开阔环境下采集多组动态GNSS观测数据,利用最小二乘和卡尔曼滤波两种估计方法进行单点定位解算,并使用Allan方差分析其在不同滤波方式下的定位误差大小和类型。将GNSS天线搭载在移动车辆顶端,驾驶车辆在测试场地按照正常驾驶车速前行,测试路线如图 1所示,GNSS天线接收频率为2 Hz。本文采用的参考系统为NovAtel公司的SPAN-LCI分体移动惯性组合导航系统,具有良好的定位精度。
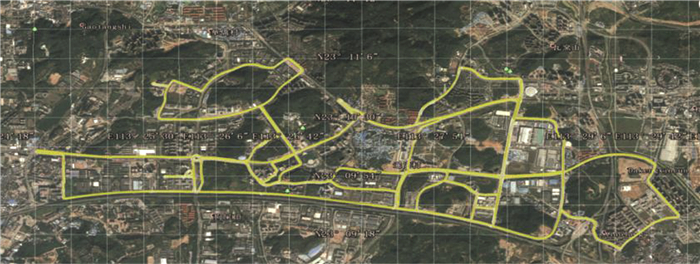 |
| 图 1 开阔环境测试轨迹 Fig.1 Open Environment Test Track |
如图 2(a)、2(c)所示,基于最小二乘估计算法解算的GNSS位置误差呈现无序分布,RMS(root mean square)较大;基于卡尔曼滤波估计算法解算的GNSS位置误差较平滑,且RMS较小。基于最小二乘估计算法解算的GNSS位置呈现散点分布,无法用于自主导航,且复杂场景时,定位误差较大。基于卡尔曼滤波估计算法解算的GNSS结果连续,能用于自主导航。
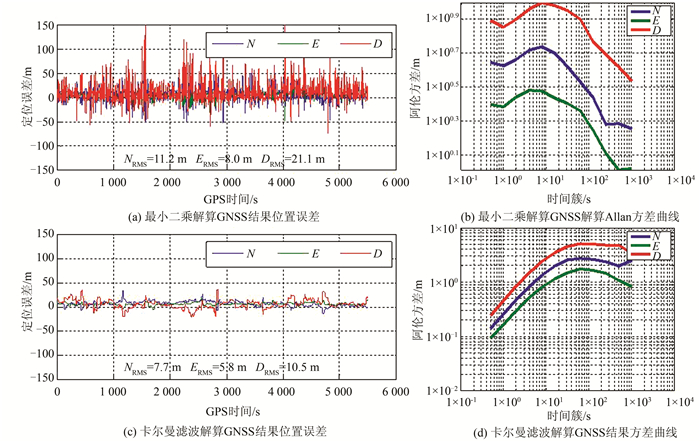 |
| 图 2 开阔环境基于不同估计方法的GNSS导航结算误差 Fig.2 GNSS Navigation Error Based on Different Estimation Methods in Open Environment |
如图 2(b)、2(d)所示,利用Allan方差对两种估计方法下解算的GNSS位置误差分析可以发现,基于最小二乘估计方法解算的GNSS位置误差类型主要为白噪声,基于卡尔曼估计方法解算的GNSS位置误差表现出较强的相关性,可以认为一阶高斯马尔科夫过程为其主要噪声模型。
基于卡尔曼滤波估计方法的GNSS单点解算结果具有定位误差小的优势,目前GNSS用户设备多使用了导航滤波器。基于最小二乘估计方法的GNSS单点解算结果虽然误差较大,但其符合GNSS/INS组合模型对观测噪声类型的要求,是否适合GNSS/INS组合导航需求还有待考证。
3 不同估计方法下GNSS导航解算结果用于GNSS/INS组合导航分析在多组开阔路段测试环境的基础上,本文将增加综合路段(包括典型城市场景)下的路测来评估两者在实际运用时的性能(图 3),综合路段位于广州市区内(图 1)。本文基于文献[12]进行GNSS/INS组合导航数据。
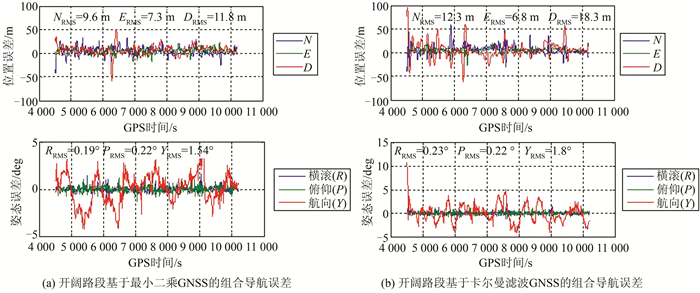 |
| 图 3 开阔场景基于不同估计方法的GNSS导航解算结果用于组合导航性能 Fig.3 GNSS Navigation Solution Based on Different Estimation Methods for Open Navigation |
如图 3所示,当测试线路位于开阔路段(图 1,GNSS观测条件相对较好)时,基于最小二乘滤波估计方法的GNSS单点解算位置结果用于组合导航后,组合导航系统水平位置精度和航向精度相较于基于卡尔曼滤波的并无明显优势,但在高程上有显著提高。考虑到基于最小二乘滤波估计方法的GNSS解算结果位置误差较大,通常会选择基于卡尔曼滤波估计方法的GNSS数据用于导航。大量试验和数据分析表明,基于最小二乘估计方法的GNSS解算结果也能用于组合导航。
考虑到车载导航实际工作情况,补充开阔路段实验后,基于上述两种不同估计方法的GNSS解算结果用于组合导航后,如图 4所示。从图 4以及统计值(图 5)可以发现,在城市综合场景时,使用里程计以及序列观测等辅助信息,基于最小二乘估计方法的GNSS解算结果用于组合导航在水平精度上,与基于卡尔曼估计方法的GNSS解算结果用于组合导航相当,但在垂向上要稍优,并且在速度和姿态上基本一致。
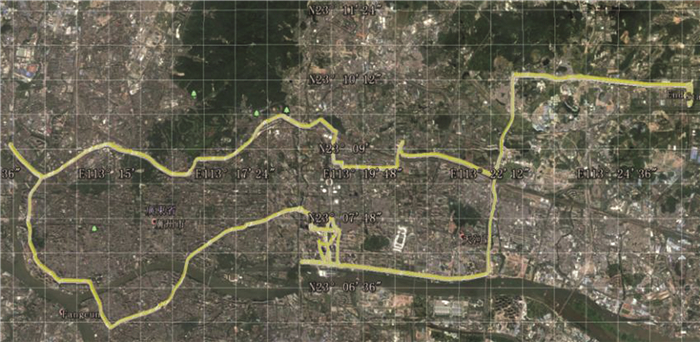 |
| 图 4 综合环境测试轨迹 Fig.4 Integrated Environment Test Track |
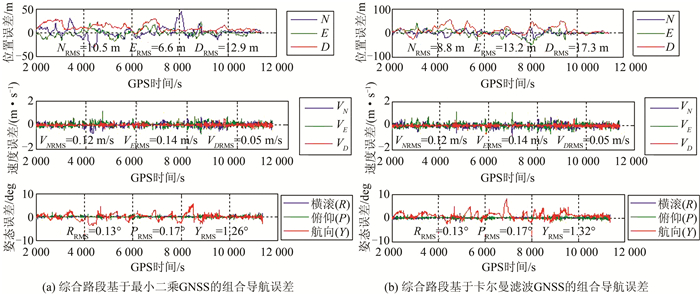 |
| 图 5 综合场景基于不同估计方法的GNSS导航解算结果用于组合导航性能 Fig.5 GNSS Navigation Solution Based on Different Estimation Methods for Integrated Navigation Performance |
4 结束语
本文通过理论分析和实测数据,证明基于最小二乘的GNSS单点解算结果能被用于GNSS/INS组合导航,主要通过Allan方差分析了基于两种估计方法的GNSS定位误差大小和类型,研究表明,基于最小二乘估计方法下GNSS单点解算定位误差较大,主要噪声类型表现为白噪声;基于卡尔曼滤波估计方法的GNSS单点解算定位误差较小,主要噪声类型表现为随机游走。实测数据进行组合导航结果表明,基于最小二乘的GNSS单点解算结果相对于基于卡尔曼滤波的GNSS单点解算结果,也能够用于采用标准卡尔曼滤波的GNSS/INS组合导航。
| [1] |
Antonio A. GNSS/INS Integration Methods[D]. Calgary: The University of Calgary, 2010
|
| [2] |
Shin E H. Accuracy Improvement of Low Cost INS/GPS for Land Applications[D]. Calgary: The University of Calgary, 2001
|
| [3] |
Budiyono A. Principles of GNSS, Inertial and Multi-sensor Integrated Navigation Systems[J]. Industrial Robot, 2012, 67(3): 191-192. |
| [4] |
殷守林, 刘天华, 李航. 基于模拟退火算法的卡尔曼滤波在室内定位中的应用研究[J]. 沈阳师范大学学报:自然科学版, 2015(1): 86-90. |
| [5] |
Minha P. Error Analysis and Stochastic Modeling of MEMS Based Inertial Sensors for Land Vehicle Navigation Applications[D]. Calgary: The University of Calgary, 2004
|
| [6] |
Antonio A, Mark P, Giovanni P. Benefits of Combined GPS/GLONASS with Low-Cost MEMS IMUs for Vehicular Urban Navigation[J]. Sensors, 2012, 12(4): 5 134-5 158. DOI:10.3390/s120405134 |
| [7] |
刘娣, 薄煜明, 邹卫军. 基于时间序列的GPS误差建模及单点定位精度研究[J]. 兵工学报, 2009(6): 825-828. DOI:10.3321/j.issn:1000-1093.2009.06.029 |
| [8] |
Niu X, Chen Q, Zhang Q, et al. Using Allan Variance to Analyze the Error Characteristics of GNSS Positioning[J]. GPS Solutions, 2014, 18(2): 231-242. DOI:10.1007/s10291-013-0324-x |
| [9] |
仇立成, 姚宜斌, 祝程程. GPS/INS松组合与紧组合的实现与定位精度比较[J]. 测绘地理信息, 2013, 38(3): 17-19. |
| [10] |
Naser E, Hou H, Niu X. Analysis and Modeling of Inertial Sensors Using Allan Variance[J]. IEEE Transactions on Instrumentation and Measurement, 2008, 57(1): 140-149. DOI:10.1109/TIM.2007.908635 |
| [11] |
张秋昭. GPS辅助SINS动态对准关键模型研究[D].徐州: 中国矿业大学, 2013 http://www.bookask.com/book/2179006.html
|
| [12] |
Niu X, Zhang Q, Gong L, et al. Development and Evaluation of GNSS/INS Data Processing Software for Position and Orientation Systems[J]. Survey Review, 2015, 47(341): 87-98. DOI:10.1179/1752270614Y.0000000099 |
 2019, Vol. 44
2019, Vol. 44


