| 数字水准仪室内快速检校的原理与方法 |
随着数字水准仪在高精度水准测量领域的广泛应用,为确保使用精度,对数字水准仪的精确检定和校准一直是仪器使用者和检定机构亟待解决的问题。数字水准仪之所以会被用于高精度水准测量,与其高灵敏度光学机械装置和高精度的传感器装置息息相关,这些装置的损坏或失准,将直接影响数字水准仪的使用精度。目前,国内数字水准仪的生产正在起步,研究数字水准仪的原理和光、机、电结构,构建室内检校专用装置,探索快速检校方法代替室外方法,免去室外需要配套条码尺、固定场地和环境等要求,提升检校精度和效率,对数字水准仪的普及发展和保障高精度水准测量结果具有重要意义。
1 数字水准仪原理及误差当前,徕卡、天宝(蔡司)、拓普康、索佳4类数字水准仪在国内占主要市场,它们所对应的水准标尺编码、解码方法不尽相同,内部构造也各不相同,但光、机、电结构基本相同,除了基本的光学机械装置,均以补偿器和电荷耦合器件(charge coupled device, CCD)传感器为核心部件。CCD传感器是一种高灵敏度的光敏装置,也是一种图像采集处理系统[1]。传感器接收到光信号后,可将光信号转换成电信号,然后由模数转换器(C/D)将模拟信号转换成数字信号供处理器处理输出。当水准标尺的编码影像被CCD识别后,将进行阅读和处理,由编码影像一步步转换成测量数据结果。
各类数字水准仪常见故障主要有补偿器超限、电子i角超限、无法测量读数、视距失准等。以上问题的产生均与CCD轴与视准轴的一致性有关。确切地说,如果观测的条码图像与到达CCD的图像不一致,或者经过补偿器到达CCD的信号与仪器内存的参考信号不一致,均有可能出现以上问题。由于数字水准仪光学部件、机械部件和电子部件互相关联,以上问题均不会因独立部件的故障产生,仪器所表现出来的电子读数误差是光机电系统产生的综合误差。因此,在数字水准仪的检校中,不仅要对仪器的光学性能进行检校,还要对电子性能进行检校,尤其是光学i角的校正、电子i角的校正和电子补偿误差的精确测定[2]。
2 数字水准仪室内检定装置数字水准仪以获取编码水准标尺的影像进行测量结果的计算,不同数字水准仪可直接以不同编码水准标尺的影像作为测量目标[3-5]。将实物测量目标变为数字测量目标,从而完成室外到室内的模拟。文献[2]基于平行光管构建了一套数字水准仪室内检定装置。该装置以焦距为1.2 m的两台平行光管作为一对平行光管组,以平行光管的目标分划板作为各类条码水准标尺影像的载体,以四维微倾工作台作为数字水准仪的安置台,整体构成一套数字水准仪的检定系统。以LEICA、TRIMBLE(ZEISS)、TOPCON和SOKKIA这4种常用的数字水准仪的编码标尺作为综合观测目标微缩到平行光管的目标分划板上[6]。为了满足数字水准仪电子i角和补偿性能的检定,确定数字水准仪测量调焦视距在15 m和30 m的两个位置对应的平行光管的分划板的两个焦距位置,两个焦距位置分别安装15 m和30 m的视距的分划板,在每个分划板上定制4幅标尺的编码影像,近焦(15 m)分划板上为视距为15 m的编码影像,远焦(30 m)分划板上为视距为30 m的编码影像。编码影像大小以数字水准仪的可测视场范围定制。检校时,数字水准仪只需按照程序指示或规程要求,调焦照准对应的编码标尺影像,即可实现测量读数,完成数字水准仪的电子i角、补偿性能等电子项目的检定。
数字水准仪的电子i角和补偿性能是评价其光电系统测量精度的重要指标,想要精确检验这两种性能对检定装置的精度要求也比较高。首先,应该保证目标分划板垂直,在竖直方向上与水准仪目镜分划板平行。其次,要保证平行光管的平直度小于1″,这就要求在同一平行光管测量近距离(15 m)和远距离(30 m)的目标时,测得的尺高应该大致相同,高差应该小于0.1 mm,确保远、近距离的分划板在同一条水平线上。
经过长期的测试,该装置稳定、可靠,可作为高精度数字水准仪的检定、校准和维修平台,克服了在室外检定的诸多局限性。
3 室内快速检校的关键技术与方法 3.1 补偿误差快速精确测定补偿误差的检校以测定仪器相对整平状态倾斜某个角度时测高读数的变化量为目的,精确整平仪器是前提和关键,使补偿器零位对应仪器置平状态。实践证明,数字水准仪左倾、右倾一定角度时,由于补偿器的回补作用,对测高影响很小;前倾、后倾时,与补偿器的摆动方向和视准轴方向一致,因而对测高影响较大。补偿器只能在一定范围内将视准轴回补到置平状态的水平位置。仪器倾斜β角度的补偿误差为:
| $ \Delta \alpha = \frac{{\Delta h \cdot \rho }}{{S \cdot \beta }} $ | (1) |
式中, Δh为仪器倾斜与置平状态时高差,单位为mm;S为检定时仪器至标尺的距离;β为仪器倾斜的角度; ρ为206 265″,Δα单位为(″/′)。
室内测定补偿误差时,借助于数字水准仪检定装置的微倾工作台,微倾螺旋4个维度倾斜分度值为1′,相对于室外目测估计气泡偏移量,使仪器倾斜角度做到可以量化控制,同时室内不受气候环境和场地的限制,使检定环境更加稳定可靠。
经过室内外对比试验,室内补偿误差测定借助微倾螺旋实现仪器的倾斜和复位,可以快速定量地将仪器倾斜到所需角度并可快速置零复位,而室外通过手动旋转仪器脚螺旋的方法倾斜复位仪器,需要匀速旋转脚螺旋同时观察估读水准气泡的倾斜量,当气泡的倾斜量到达估计位置停止旋转脚螺旋,整平复位时也是依靠脚螺旋。试验结果显示,室外法耗时耗力,结果不稳定,而室内法省时省力,检校效率可以提升一半,并能够保证检校结果的精度和可靠性。
3.2 电子i角快速测定和校正仪器i角也就是视准线(视准轴)倾斜误差。数字水准仪在自安平水准仪的基础上,引入了光电结合误差。因此,传统意义上对水准仪i角的定义已经不能完全解释数字水准仪的i角了。数字水准仪具有光学视准轴和电子视准轴两个视准轴。光学视准轴等同于常规的自安平水准仪的视准轴,即物镜光心和十字丝中心的连线。电子视准轴,是物镜光心和CCD传感器中心附近的一个参考像素的连线。光学视准轴与光学i角形成有关,电子视准轴与电子i角形成有关。
过物镜光心的水平入射光线经过补偿器后形成一条准绝对水平视准线,而这条准绝对水平光线在分光镜的作用下会分成两路,一路成像在CCD上,形成电子i角(电子视准轴与准绝对水平视准线的夹角);一路成像在目镜分划板上,形成光学i角(光学视准轴与准绝对水平视准线的夹角)。光学i角可经过校正目镜十字丝改正,而电子i角则需要通过仪器给定的方法把其真实值测定并存储到仪器中。实践证明,校正仪器十字丝并不能彻底改正电子i角,把仪器电子i角当做光学i角处理,也是目前对数字水准仪i角认知的一个误区。补偿器的出射主光轴中心位置与CCD传感器的像素中心位置的一致性决定了电子i角的大小和精度。由于CCD传感器初始位置固定,补偿器决定了准绝对水平线的准确程度,而这条准绝对水平线的准确程度又决定了仪器i角的大小和稳定性。因此,电子i角的校正就是精确测定电子视准轴与准绝对水平线的夹角大小,体现到仪器中就是对测高读数影响量。实际上,本文校正电子i角就是利用仪器内置方法精确测定电子i角的真实值,将其作为改正值存储下来,以便修正i角对仪器测高读数的影响,从而达到校正电子i角的目的。
在室内检定平台上快速检定电子i角时,以费式法(Foerstner)为例[7, 8], 即将两根标尺(A、B)安置在相距45 m的距离,将其3等分,在距标尺15 m处设两个站(站1和站2),定义h1a、h1b、h2a、h2b分别是仪器在站1和站2测得的标尺A、B的视线高,d1a、d1b、d2a、d2b分别是仪器在站1和站2测得的标尺A、B的视距。本文采用单光管检校电子i角,模拟理想状态下室外的检校条件,变站不升降仪器,相当于仪器架设在等高的两个站上,拟定15 m和30 m条码分划分别为A、B尺,则hA、hB分别为15 m和30 m条码分划测得的视线高,有h2a=h1b=hB,h1a=h2b=hA。因此,电子i角计算公式可定为:
| $ \begin{array}{*{20}{c}} {i = \arctan \frac{{\left( {{h_{1a}} - {h_{1b}}} \right) - \left( {{h_{2a}} - {h_{2b}}} \right)}}{{\left( {{d_{1a}} - {d_{1b}}} \right) - \left( {{d_{2a}} - {d_{2b}}} \right)}} \approx }\\ {\frac{{2\left| {{h_A} - {h_B}} \right|}}{{30}} \cdot \rho = \frac{\rho }{{15}} \cdot \Delta {h_{AB}}} \end{array} $ | (2) |
由于i角的大小取决于仪器在两站测得的高差的变化量,变化量越大i角越大,这里计算出的电子i角实际是i角校正值的残差,i角的真实值将作为修正值存进仪器。由式(2)可推算出室外基准环境下电子i角与两测站高差变化量Δh的关系,如式(3)所示;同理,由式(2)可推算出室内基准环境下电子i角与两测站高差变化量ΔhAB的关系,如式(4)所示,ΔhAB为室内单光管远(30 m)、近(15 m)目标的测量高差。
| $ \begin{array}{*{20}{c}} {\Delta h = \left( {{h_{1a}} - {h_{1b}}} \right) - \left( {{h_{2a}} - {h_{2b}}} \right) \approx }\\ {1.45 \times {{10}^{ - 4}} \cdot i}\\ {} \end{array} $ | (3) |
| $ \Delta {h_{AB}} \approx 7.27 \times {10^{ - 5}} \cdot i $ | (4) |
依据式(3)和式(4)可将电子i角限差归算到A、B尺的读数高差变化量的限差,如表 1所示。因此,在室内只需要两个读数hA和hB,就可以快速判断电子i角是否超限,若超限,则根据仪器指定方法校正电子i角。
| 表 1 数字水准仪电子i角限差归算 Tab.1 Tolerance Reduction of Electronic i Angle on Digital Level |
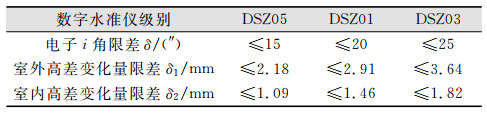 |
表 1中,δ为检定规程对电子i角限差的规定;δ1为室外基准环境下检测电子i角允许的两测站高差变化量限差;δ2为室内单光管法检校电子i角允许的远(30 m)、近(15 m)目标的测量高差限差。
经过长期大量的室内外电子i角的检校比对试验,结果表明,室内检校环境比室外检校环境的影响因子更小,不受场地、时间、天气的限制,节省了大量的人力物力,在检校效率的提升上尤为突出。如表 2所示,电子i角检校过程的耗时比对试验,室内单光管法和室外法在各个检校过程的耗时比对。
| 表 2 室内外检校过程耗时比对/min Tab.2 Comparison the Time of Indoor and Outdoor Calibration Process/min |
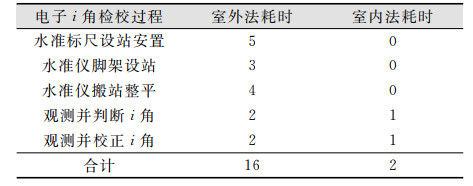 |
由表 2的比对试验分析,室内法借助专用平行光管检校装置,相对于室外法省去了水准标尺、脚架的架设时间,同时室内单光管法也省去了室外数字水准仪搬站整平的时间,在电子i角的判断和校正过程中,室内法在观测读数时也可以节省一半时间。因此,电子i角的检校室外法需要16 min左右,而室内法只需要2 min左右的时间就可以完成检校,实现了快速检校,有效提升了电子i角的检校效率。
3.3 快速检验CCD位移的方法当数字水准仪出现对准标尺条码带中央无法测量读数或远距离无法测量读数的问题,常与CCD的位置有关。当CCD发生位移或倾斜时,CCD接收到的测量信号与目镜所观测的信号不完全一致,包括一些无效的测量信号。从而无法从参考信号中搜索到与CCD接收到的测量信号一致的编码信号,无法计算出测量结果,就会出现无法测量读数的问题。图 2中,直线O对应CCD传感器的中线位置,测量所需的视场范围为b,当CCD向右倾斜角度α时,对准标尺左边缘、中央时所对应的CCD位置分别为直线B、C,CCD捕捉到的有效视场为b、c。由图 1可以看出,对准标尺中央时,有效视场不足,会出现无法测量现象,而在标尺左边缘又可以测量,再往左甚至会出现尺外测量现象。而右边缘往右完全超出了CCD的信号捕捉范围,也无法测量。因而,这种情况下必须校正CCD的位置,使其垂直,保证在标尺左边缘、中央、右边缘均可以测量,并且测得的视线高差异小。
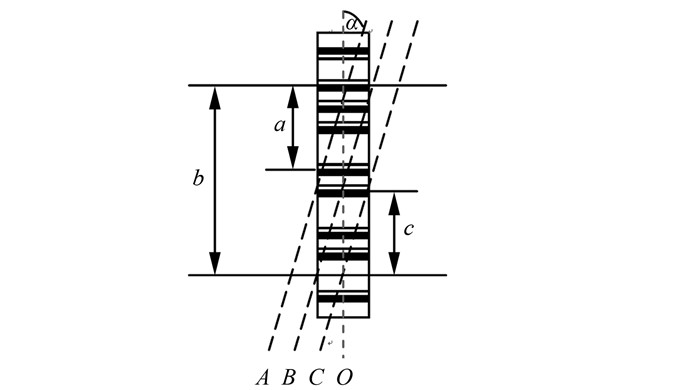 |
| 图 1 CCD位置倾斜时的可测量视场变化 Fig.1 Measurable Field Variation of CCD Tilt |
如表 3所示,CCD传感器的出厂位置有4个自由度和一个常数位置[9],其中常数位置有两方面的表述。第一,CCD的信号采集平面应该与望远镜的焦平面重合,即CCD的焦线垂直于望远镜的焦点。这个位置决定着测距的精确度。第二,CCD传感器的中点位置应该与补偿器的出射主光轴的中心一致(大致处于一条直线上),这个位置决定着电子i角的大小[10, 11]。其他4个自由度的变化,均与仪器的测量读数、电子i角、补偿性能等有关。因此,可通过的故障显示快速进行故障分析,判别CCD的位置变化。CCD传感器的位置决定了数字水准仪的可测量性和精度,CCD校正这种极少见的机械故障可返厂维修或交由专业机构进行校准。
| 表 3 CCD位置变化对仪器产生的影响 Tab.3 CCD Position Change on the Impact of the Instrument |
 |
4 结束语
综合上述讨论分析,对于数字水准仪的检校,可借助室内数字水准仪检定专用装置,快速评估仪器的性能,完成电子i角、补偿误差等项目的检定,实现了基于仪器读数故障检验CCD位置的变化的方法,有效提升了仪器检校的精度和效率,克服了室外检校的局限性,比室外检校方法具有更高的效率,有较好的推广和参考价值。
| [1] |
刘经南, 叶晓明, 杨蜀江. 数字电子水准仪原理综述[J]. 电子测量与仪器学报, 2009(7): 89-94. |
| [2] |
庞尚益, 吴学文, 杨坤, 等. 数字水准仪室内检定装置[J]. 测绘通报, 2012(S1): 218-220. |
| [3] |
陈耿彪, 乌建中, 乐韵斐. 数字水准仪标尺编码原理研究[J]. 测绘学报, 2008, 37(3): 380-383. |
| [4] |
肖进丽, 李松, 胡克伟. 几种数字水准仪标尺的编码规则和读数原理比较[J]. 测绘通报, 2004(10): 57-59. |
| [5] |
郭金运, 徐泮林, 曲国庆. 数字水准仪的性能比较与分析[J]. 测绘通报, 2002(3): 55-57. |
| [6] |
路杰, 付辉清, 欧同庚, 等. 一种新型数字水准仪室内检定装置[J]. 大地测量与地球动力学, 2007(S1): 96-97. |
| [7] |
罗官德, 任道胜, 陈如丽. 数字水准仪i角检校方法探讨[J]. 测绘信息与工程, 2002, 27(4): 45-47. |
| [8] |
王美婷. 数字水准仪i角检定方法比较分析[J]. 计量与测试技术, 2017, 44(9): 66-67. |
| [9] |
杨俊志, 刘宗泉. 数字水准仪的测量原理及其检定[M]. 北京: 测绘出版社, 2005.
|
| [10] |
国家测绘地理信息局.数字水准仪量检测定规程: JJG425-2003[S].北京: 中国计量出版文化, 2003
|
| [11] |
曾征.电子水准仪室内检定方法的研究[D].广州: 华南理工大学, 2012
|
 2020, Vol. 45
2020, Vol. 45

