| 一种改进选点策略的RANSAC圆柱面检测算法 |
2. 浙江省国土勘测规划有限公司,浙江 杭州,310000
2. Zhejiang Land Survey & Planning Co., Ltd., Hangzhou 310000, China
利用三维激光扫描技术能快速、高效地获取物体表面的三维坐标信息,被广泛应用于地铁隧道形变监测、滑坡监测、文物保护、建筑物三维重建、自动驾驶等领域[1-5]。在大量无规则点云数据中快速检测出其中包含的基本形状,有利于对物体进行快速分类,可用于物体的非监督分类[6]。现实中有很多物体包含圆柱体形,如何快速得到圆柱体的模型参数并将其用于三维重建或分类是一个热门问题。利用几何模型方法,用圆柱模型的数学表达式建立误差方程,进而求得圆柱模型参数[7-9],不太适用于大数据量的点云模型检测。利用圆柱体的高斯特性可将提取过程分为两个阶段进行特征参数提取[10];采用遗传算法可以实现圆柱几何特征信息全局最优解的评定[11];利用随机抽样一致(random sample consensus,RANSAC)算法拟合圆柱面,在点云中将两点作为种子点进行圆柱面的检测,不能保证选取的两个点的质量,影响计算得到的模型参数[12]。基于RANSAC的算法得到的模型参数有很好的鲁棒性,能从包含大量局外点的数据集中估计出较高精度的参数。考虑到点云数据量大且其中可能包含大量噪声点,本文提出了一种基于改进选点策略的RANSAC圆柱面检测算法。
1 传统基于RANSAC的点云圆柱面检测 1.1 k维树k维树(k-dimensional tree,KD-Tree)是k维的二叉树索引,主要用于检索多属性的数据或多维数据。与二叉树不同的是,KD-Tree的每个结点均表示k维空间的点。如当k=3时,每个结点表示一个三维坐标(X,Y,Z)。KD-Tree能像二叉树一样,按照一定的索引规则完成点的精确查找,由每个内部结点决定搜索走向,最终搜索到所查询的结点的块。索引结构中相似性查询有两种基本的方式:①R半径查询:通过提供查询点、查询距离的阈值,得到一个数据集合,其中每个数据都小于给定的阈值;②k最近邻(k-nearest neighbor,KNN)个数查询:通过KNN得到一个包含K个数据的,距离查询点最近的点的集合[13]。
1.2 点云法向量估计点云法向量估计最常用的方法是协方差分析法,对于点云中的点pi及其K邻域点集Kn(pi)(邻域点可通过KD-Tree空间查询得到),构造Kn(pi) 的协方差矩阵Ci:
| $\left\{\begin{array}{l} \boldsymbol{C}_{i}=\sum\limits_{p \in K_{n}\left(p_{i}\right)}\left(p-o_{i}\right)\left(p-o_{i}\right)^{\prime} \\ o_{i}=\frac{1}{n} \sum\limits_{p \in K_{n}\left(p_{i}\right)} p_{i} \end{array}\right. $ | (1) |
式中,Ci为对称正定矩阵,其特征值为(λ0,λ1,λ2),对应的3个特征向量(e0,e1,e2)相互正交,最小特征值λ0所对应的特征向量e0即为最优平面的法向量,可作为pi的法向量[14, 15]。
1.3 圆柱面拟合为了用任意两点及其法线生成一个圆柱面,首先确定轴的方向a(l,m,n),a=n1 × n2,其中,n1、n2分别为圆柱体表面的任意两点p1、p2的法向量。将两条法线p1+tn1和p2 + tn2沿轴线方向投影到ax=0平面上,两条投影线相交得到点p12。由此可以得到中轴线的直线表达式。应用阈值、点到圆柱体轴线的距离来判断局内点。统计满足该模型参数的点云个数,在满足局内点个数阈值的圆柱体中寻找标准差最小的圆柱体,得到最佳拟合圆柱体。圆柱面示意图见图 1。
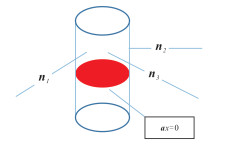 |
| 图 1 圆柱面示意图 Fig.1 Diagram of Cylindrical Surface |
2 改进选点策略的RANSAC圆柱面检测 2.1 改进的种子点选取方式
传统基于RANSAC算法的圆柱面参数通过空间中两个点来确定,该算法的选点方式是从原始数据点中随机选出两个点作为种子点,获取圆柱面模型参数的初始值,再根据初始值寻找数据中其他的模型内点。该方法得到的参数模型稳健性较差,受点云数据质量的影响较大。在采样次数一致情况下,满足判断准则的圆柱面模型的数据集减少了,降低了得到最优模型的概率。本文提出的改进种子点选取方式是随机选取3个点,通过KD-Tree建立的索引寻找每个点R半径内的邻域点集Kn,采用协方差分析法来求得这3个点的法向量,并根据判断准则得到模型参数的初始值。
2.2 模型参数判断准则依据两点作为种子点方法得到的圆柱体参数模型绝大多数不满足判断准则,考虑在模型参数初始值的选取上利用3个点的法向量来构造初始值:
| $ \left\{\begin{array}{l} \boldsymbol{a}_{1}=\boldsymbol{n}_{1} \times \boldsymbol{n}_{2} \\ \boldsymbol{a}_{2}=\boldsymbol{n}_{2} \times \boldsymbol{n}_{3} \\ \theta=\arccos \left(\boldsymbol{a}_{1} \times \boldsymbol{a}_{2}\right) \end{array}\right. $ | (2) |
式中,n1、n2、n3表示过3点的法向量;a1、a2是由法向量n1、n2、n3构造的轴线方向。对于规则光滑的圆柱体表面,理论上a1 =λ× a2,考虑到获取的圆柱体表面点云数据存在噪声,引入两条轴线的夹角这一判断准则:若θ < θ0(角度阈值),则轴线方向a=a1+ a2,a为两个向量的合向量。这样可以抑制部分噪声,优化模型初始值的计算。
将3条法线p1 + tn1、p2+tn2、p3+tn3沿轴线方向投影在ax=0平面上,理论上3条法线在该平面上的投影应交于一点,实际得到两两相交的3个点。将得到的3点组成一个三角形,若三边d12、d13、d23的距离均小于阈值d,则求三角形的重心c,否则重新选取3个点,得到新的模型参数。
设3个点在投影平面的投影点坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3),则重心c的坐标(Xc,Yc,Zc)计算公式如下:
| $ \left\{\begin{array}{l} X_{c}=\frac{1}{3}\left(x_{1}+x_{2}+x_{3}\right) \\ Y_{c}=\frac{1}{3}\left(y_{1}+y_{2}+y_{3}\right) \\ Z_{c}=\frac{1}{3}\left(z_{1}+z_{2}+z_{3}\right) \end{array}\right. $ | (3) |
本文方法要对点云数据进行多次抽样,在抽样结束后比较θ和dmax,将θ最小和dmax最大的那组数据得到的模型参数作为最佳模型参数。具体算法流程见图 2。
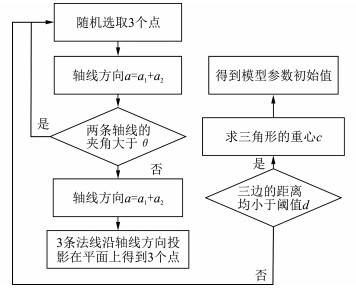 |
| 图 2 本文方法流程 Fig.2 Flow Chart of the Proposed Method |
3 仿真实验
以真实值为半径(R=2 m),中轴线方向为L(0,0,1),过点P(0,0,0)构造的圆柱面点云个数CP为2 000、5 000、10 000、20 000、50 000、100 000、200 000的点云数据,并加入一定比例S的噪声点(S=N/CP),N表示加入的噪声点个数。图 3和图 4分别展示了未加入噪声点和加入噪声点后的完整圆柱面点云数据,考虑实际获取的圆柱面点云数据可能只是整个圆柱面的一部分,本文构造了图 5所示的点云数据。
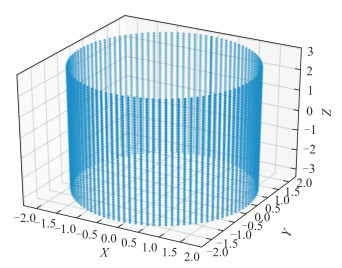 |
| 图 3 未加入噪声点的完整柱面 Fig.3 Complete Cylindrical Surface Without Noise Points |
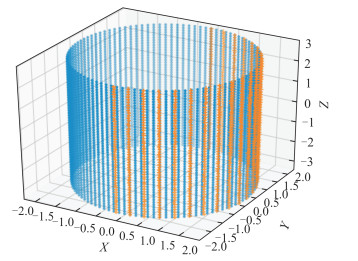 |
| 图 4 加入噪声点的完整柱面 Fig.4 Complete Cylindrical Surface with Noise Points |
 |
| 图 5 加入噪声点后的部分圆柱面点云数据 Fig.5 Point Cloud Data of Partial Cylindrical Surface After Adding Noise Points |
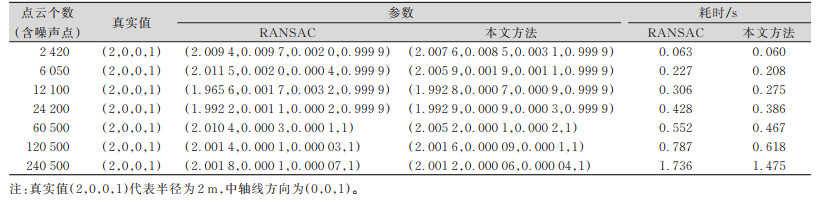
用基于RANSAC拟合圆柱面的方法和基于改进选点策略的RANSAC圆柱面检测方法分别处理仿真得到的点云数据,当S < 0.50时,得到了比较一致的实验结果。本文给出了当S=0.21时,两种方法处理得到的模型参数和处理所需时间,见表 1。
| 表 1 模型参数和耗时 Tab.1 Model Parameters and Time Consumption |
 |
为了更直观地比较本文方法和传统基于RANSAC拟合圆柱面方法的效果和效率,本文利用Python的matplotlib包给出了不同点云数量下的处理时间,见图 6。不同点云数量下的拟合半径图见图 7。
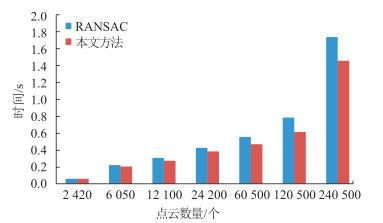 |
| 图 6 耗时 Fig.6 Time Consumption |
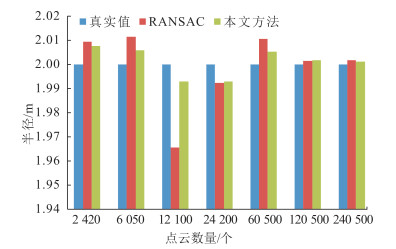 |
| 图 7 拟合半径 Fig.7 Fitting Radius |
在不同点云数量下,本文方法比传统基于RANSAC的方法耗时要少,在点云数量较少时,两者差距很小,但随着点云数量的增加,两者的检测速度差距也逐渐增大,当点云数据中包含多个需要检测的圆柱面点云数据时,两者的效率差距会更明显。
存在噪声时,利用两种方法都可以拟合出圆柱体的半径,且拟合出来的半径大小具有较好的一致性,这说明两种方法受噪声的影响是基本一致的。但是传统基于RANSAC拟合圆柱面半径的方法不够稳健,在点云数量为12 100时,拟合出来的半径和实际半径相差34.4 mm,在点云数量为120 500时,拟合出来的半径和实际半径仅相差1.4 mm。同样,本文方法在点云数量为12 100时拟合的半径和实际半径相差最大,这说明噪声点对利用两种方法得到的半径都产生了影响,但本文方法稳定性更好,在不同点云数量下都可以较好地接近真实值。
4 结束语本文提出了一种基于改进选点策略的RANSAC圆柱面检测方法,在采样次数一致的情况下,根据给定规则,提高了得到最优模型参数的概率和效率。将随机获取的点云数据按照给定规则进行筛选,进而当作种子点,用于计算模型参数,能有效地提高模型参数初始值的质量。实验结果表明,该方法能提高模型检测的速度和模型参数的质量。
| [1] |
姚艳丽, 蒋胜平, 王红平. 基于地面三维激光扫描仪的滑坡整体变形监测方法[J]. 测绘地理信息, 2014, 39(1): 50-53. |
| [2] |
Schnabel R, Degener P, Klein R. Completion and Reconstruction with Primitive Shapes[J]. Computer Graphics Forum, 2009, 28(2): 503-512. DOI:10.1111/j.1467-8659.2009.01389.x |
| [3] |
宋碧波, 卢小平, 卢遥. 基于点云数据的建筑物三维重建[C]. 测绘科学前沿技术论坛, 长春, 2010
|
| [4] |
叶语同, 李必军, 付黎明. 智能驾驶中点云目标快速检测与跟踪[J]. 武汉大学学报·信息科学版, 2019, 44(1): 139-144. |
| [5] |
宋红霞, 侯妙乐, 胡云岗. 文物保护中海量点云数据库设计与开发[J]. 城市勘测, 2014(1): 89-93. |
| [6] |
张坤, 乔世权, 周万珍. 基于三维形状匹配的点云分割[J]. 激光与光电子学进展, 2018, 55(12): 263-274. |
| [7] |
王解先. 工业测量中一种二次曲面的拟合方法[J]. 武汉大学学报·信息科学版, 2007, 32(1): 47-50. |
| [8] |
严宇, 王解先. 激光扫描点云数据的圆柱拟合方法[J]. 测绘科学, 2018, 43(6): 83-87. |
| [9] |
曹星星, 刘常弘, 邱建平. 基于逆向工程原理的圆柱体构件定位方法研究[J]. 江西测绘, 2015(4): 63-64. |
| [10] |
刘元朋, 张定华, 张力宁. 逆向工程中圆柱体提取方法的研究[J]. 计算机辅助设计与图形学学报, 2005, 17(9): 1 946-1 949. |
| [11] |
李学军, 常智勇, 莫蓉, 等. 基于遗传算法的圆柱几何特征信息的测量[J]. 计算机工程与应用, 2006, 42(22): 56-58. |
| [12] |
Schnabel R, Wahl R, Klein R. Efficient RANSAC for Point-Cloud Shape Detection[J]. Computer Graphics Forum, 2007, 26(2): 214-226. |
| [13] |
路明月, 何永健. 三维海量点云数据的组织与索引方法[J]. 地球信息科学, 2008, 10(2): 190-194. |
| [14] |
李宝, 程志全, 党岗, 等. 三维点云法向量估计综述[J]. 计算机工程与应用, 2010, 46(23): 1-7. |
| [15] |
张强, 李朝奎, 李俊晓, 等. 一种改进的基于法矢方向调整的平面点云分割方法[J]. 地理与地理信息科学, 2015, 31(1): 45-48. |
 2022, Vol. 47
2022, Vol. 47

