| 格网法在2000国家大地坐标系基准转换中的关键技术 |
随着空间大地测量技术的不断更新,不同基准的坐标系统逐渐形成,我国先后建立了起了1954年北京坐标系、1980西安坐标系以及2000国家大地坐标系[1]。2018年7月1日起全面统一使用2000国家大地坐标系,许多基于旧坐标系的坐标成果在向新坐标系转换时需要借助于坐标转换模型,由于受当时技术手段的限制,坐标系存在误差累积和扭曲变形(如浙江省1980西安坐标系建立时采用的是南北网单独平差再合并的方式),因此在使用一套参数进行全省范围的数据转换时往往得不到理想的精度,分区块转换时又存在着数据接边问题。而基于格网的坐标转换方法已经在美国、加拿大、澳大利亚等地广泛使用,原国家测绘地理信息局发布的1∶1万格网改正量和浙江省大地水准面精化模型的建立为使用格网进行平面和高程的坐标转换方法创造了条件[2]。
本文将基于格网的坐标转换方法应用在平面和高程基准转换中,并进行相关的探讨。
1 格网建立基于格网的坐标转换方法就是将一个大的区域分割成连续的标准格网单元,以4角改正量进行双线性内插以达到小范围精细拟合和大范围连续的转换效果[3]。
1.1 改正量获取一般来说,格网的分辨率越高,内插值越接近于真值,但分辨率太高,数据量巨大,就会影响到转换速度。原国家测绘地理信息局发布的1∶1万格网改正量以标准图幅为格网(见表 1)。
| 表 1 浙江省1万格网改正量/(″) Tab.1 1∶10 000 Grid Correction in Zhejiang Province/(″) |
 |
格网4个顶角均有经纬度改正量,其具体计算过程为:
| $ \left\{ \begin{array}{l} {B_{80}} + {\rm{d}}{B_{80 - 2000}}{\rm{ = }}{B_{2000}}\\ {L_{80}} + {\rm{d}}{L_{80 - 2000}}{\rm{ = }}{L_{2000}} \end{array} \right. $ | (1) |
式中,B80、L80为角点在1980西安坐标系的经纬度;角点在B2000、L2000为2000国家大地坐标系的经纬度;dB80-2000、dL80-2000为两个坐标系经纬度的差。
根据国家标准规定,我国基本比例尺地形图均以1∶100万地形图为基础,按经差6°、纬差4°划分图幅[4]。1∶100万~1∶5 000地形图编号均以1∶1 00万地形图编号为基础,采用行列编号的方法。将1∶100万地形图按所含各比例尺地形图的经差和纬差划分成若干行和列,横行从上到下、纵列从左到右按顺序分别用3位阿拉伯数字(数字码)表示,不足3位者前面补零,按行号在前、列号在后的排列形式进行标记;各种比例尺地形图分别采用不同的字符作为其比例尺代码[5, 6]。如表 1所示,G表示1∶1万比例尺,即一幅1∶1 00万地形图划分成96×96幅1∶1万地形图。据此,可以算出一幅1∶1万地形图的经差为3′45″,纬差为2′30″,计算出此图幅号的西南角经纬度值。
| $ \left\{ \begin{array}{l} L\_{\rm{{西南} = }}\left( {L - 31} \right) \times 6^\circ + \left( {l - 1} \right) \times \Delta L\\ B\_{\rm{{西南} = }}\left( {H - 1} \right) \times 4^\circ + \left( {4^\circ /\Delta B - h} \right) \times \Delta B \end{array} \right. $ | (2) |
式中,L、H为1∶100万图幅经纬度数字号;l、h为所求比例尺下图幅经纬度数字号;ΔL、ΔB为所求比例尺下经纬度差。
根据公式(2)计算出1∶1万图幅四角经纬度值,以及反算出需要转换的坐标值所落在的图幅,根据4角改正量双线性内插就能计算出所需转换坐标的改正量dL、dB。
1.2 双线性内插双线性内插法在图片转换中使用普遍,具有计算简单、转换结果平滑性好,过度自然等特点。在数学上,双线性内插是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值[7, 8]。如图 1所示,已知Q12、Q22、Q11、Q21,如要插值的点为P点,这就要用双线性插值了,首先在x轴方向上,对R1和R2两个点进行插值,然后根据R1和R2对P点进行插值。
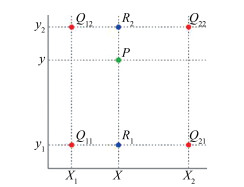 |
| 图 1 双线性内插示例图 Fig.1 Example of Bilinear Interpolation |
要计算未知函数f在点P(x,y)的值,已知函数f在Q11 = (x1,y1),Q12 = (x1,y2),Q21 = (x2,y1),Q22 = (x2,y2)这4个点的值,首先在x方向进行线性插值,得到:
| $ \left\{ {\begin{array}{*{20}{c}} {f\left( {{R_1}} \right) \approx \frac{{{x_2} - x}}{{{x_2} - {x_1}}}f\left( {{Q_{11}}} \right) + \frac{{x - {x_1}}}{{{x_2} - {x_1}}}f\left( {{Q_{21}}} \right), }\\ {{R_1} = \left( {x, {y_1}} \right)}\\ {f\left( {{R_2}} \right) \approx \frac{{{x_2} - x}}{{{x_2} - {x_1}}}f\left( {{Q_{12}}} \right) + \frac{{x - {x_1}}}{{{x_2} - {x_1}}}f\left( {{Q_{22}}} \right), }\\ {{R_2} = \left( {x, {y_2}} \right)} \end{array}} \right. $ | (3) |
然后在y方向进行线性插值,得到:
| $ f(P) \approx \frac{{{y_2} - y}}{{{y_2} - {y_1}}}f\left( {{R_1}} \right) + \frac{{y - {y_1}}}{{{y_2} - {y_1}}}f\left( {{R_2}} \right) $ | (4) |
这样就得到所要的结果f(x,y) 为:
| $ \begin{array}{l} f({\rm{x}}, {\rm{y}}) \approx \frac{{f\left( {{Q_{11}}} \right)}}{{\left( {{x_2} - {x_1}} \right)\left( {{y_2} - {y_1}} \right)}}\left( {{x_2} - x} \right)\left( {{y_2} - y} \right) + \\ \;\;\;\;\;\;\;\frac{{f\left( {{Q_{21}}} \right)}}{{\left( {{x_2} - {x_1}} \right)\left( {{y_2} - {y_1}} \right)}}\left( {x - {x_1}} \right)\left( {{y_2} - y} \right) + \\ \;\;\;\;\;\;\;\frac{{f\left( {{Q_{12}}} \right)}}{{\left( {{x_2} - {x_1}} \right)\left( {{y_2} - {y_1}} \right)}}\left( {{x_2} - x} \right)\left( {y - {y_1}} \right) + \\ \;\;\;\;\;\;\;\frac{{f\left( {{Q_{22}}} \right)}}{{\left( {{x_2} - {x_1}} \right)\left( {{y_2} - {y_1}} \right)}}\left( {x - {x_1}} \right)\left( {y - {y_1}} \right) \end{array} $ | (5) |
每个标准图幅经纬度差固定,所以公式化简为:
| $ \begin{array}{l} f(x, y) \approx \left[ {f\left( {{Q_{11}}} \right)\left( {{x_2} - x} \right)\left( {{y_2} - y} \right) + f\left( {{Q_{21}}} \right) \cdot } \right.\\ \;\;\left( {x - {x_1}} \right)\left( {{y_2} - y} \right) + f\left( {{Q_{12}}} \right)\left( {{x_2} - x} \right)\left( {y - {y_1}} \right) + \\ \left. {\;\;\;\;\;\;\;\;f\left( {{Q_{22}}} \right)\left( {x - {x_1}} \right)\left( {y - {y_1}} \right)} \right] \div 33750 \end{array} $ | (6) |
这就可从底层开发软件,实现逐点转换,且不受GIS软件平台的限制。
1.3 格网规范化对大部分使用者来说,调用NTv2格式直接用于基准间的转换则更为方便。NTv2格式由加拿大大地测量局建立。该格式已被其他几个国家采用:包括法国、德国、澳大利亚、加拿大、巴西等。国内坐标转换格网改正文件格式尚未正式确定,可借鉴采用NTv2格式作为标准格式[9],此格式兼容ArcGis和FME软件,可不用编写代码直接调用。
单个NTv2文件可以包含具有不同精度的各种格网。从格网文件中检索4个最接近的已知坐标,然后使用双线性内插进行插值。NTv2网格文件的默认扩展名是GSB(grid shift binary)。此文件有一个ASCII变种,扩展名为GSA(grid shift ASCII)。
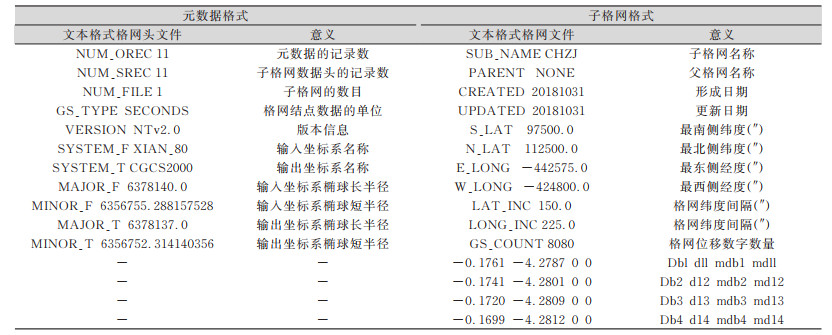
原国家测绘地理信息局发布的1∶1万格网改正量是Excel格式,可通过标准图幅号字段与浙江省测绘资料档案馆提供的1∶1万标准图幅建立连接关系,将格网图形化为SHP文件后再转换为GSA格式文件。GSA格式,dB、dL记录在单个文件中,包括元数据、子格网两部分;格网的总体结构为:元数据、子格网1、…子格网N;元数据和子格网的格式见表 2[10]。GSB格式与GSA格式是等价的,只将GSA格式中信息以二进制存储,以便计算机读取。
| 表 2 NTv2元数据和子格网格式 Tab.2 NTv2 Metadata and Sub Grid's Format |
 |
2 格网的使用
对于文本格式的文件转换采用代码编写执行效率高,而相对于常用的GIS数据进行基准转换则采用标准格式格网更为方便,而不需要在日益增多的数据格式种类和标准上花费过多的精力。在ArcGis和FME中使用格网的方法类似。将GSB文件拷贝到安装目录下的\ Reproject\GridData\China或\pedata\ntv2\China下,定义基准变换文件(见图 2)后,基准之间的转换就可以自动运行。
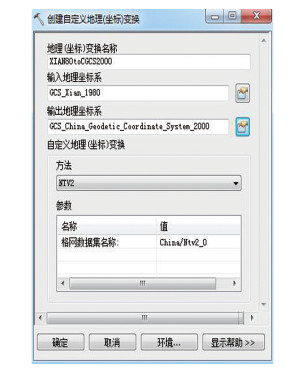 |
| 图 2 基准变换定义 Fig.2 Definition of Datum Transformation |
XFORM_DEF Xian80_to_China_2000_FME
SRC_DTM Xian80
TRG_DTM China_2000_FME
DESC_NM "China Geodetic Coordinate System 2000"
SOURCE "EPSG,V9. 2. 2,4479"
GROUP ASIA
INVERSE Yes
MAX_ITR 10
CNVRG_VAL 1e-09
ERROR_VAL 5e-08
METHOD GRID_INTERP
GRID_FILE NTv2,Fwd,. \GridData\China\ZJXIAN80CGCS2000. gsb
以1∶1万数据转换为例,在FME平台中调用坐标系转换模板,不需要考虑数据格式类型,在读模块中选择需要转换的数据就可以快速完成数据从1980西安坐标系到2000国家大地坐标系的转换。
3 精度评估为了保证高精度高分辨率格网1980西安坐标系向2000国家大地坐标系转换改正量的正确性,衡量改正量的精度,需要对改正量进行连续性与符合性进行评估。通过绘制高精度高分辨率格网1980西安坐标系向2000系转换改正量分量dB、dL分级图(见图 3)检验改正量的连续性,其连续性越好,立面图越平缓。
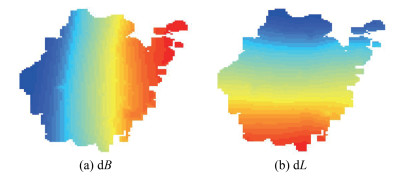 |
| 图 3 dB、dL分级图 Fig.3 Classification Diagram by dB and dL |
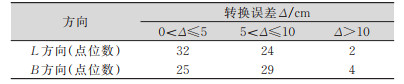
将全省86座连续运营卫星定位参考站点中含有两套成果的58个点由1980西安坐标系坐标转换为2000国家大地坐标系坐标,与站点的2000国家大地坐标系成果进行差值统计(见表 3),L方向(东方向)坐标转换中误差小于5. 7 cm,B方向(北方向)坐标转换中误差小于6. 5 cm,最小点0. 3 cm,最大点13 cm。符合转换精度要求,与浙江省2000国家大地坐标系吻合,可用于小于1∶2 000比例尺的空间数据转换,若要获取更高的精度需要在此格网的基础上加密二级格网。
| 表 3 坐标转换精度统计表 Tab.3 Accuracy Statistics for Coordinate Transformation |
 |
4 结束语
1)因受基础条件限制,以前建设的地面控制点分布不均,合并后存在着不均匀变形情况,采用格网内插法比相似变换和多项式变换精度高,转换不受比例尺及范围的限制,可转换任意比例尺、任意范围大小的地理信息数据,且任意比例尺同一地理位置的转换结果相同,转换为无缝转换,不需要重新接边。
2)为获得更高的精度,可在国家基本格网的基础上,针对不同区域在此基础上建立不同精度、不同密度的子格网以满足基准转换的多样化、差异化需要。格网可采用分块分割一定程度上满足了保密的要求。
3)将经纬度改正量换成大地高改正量,本模型可直接应用在大地水准面精化计算。
4)该方法已成功应用在浙江省2000国家大地坐标转换以及浙江省卫星导航定位基准服务格网发布中。
| [1] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 国家基本比例尺地形图分幅和编号: GB/T 13989-2012[S]. 北京: 中国标准出版社, 2012
|
| [2] |
郭充, 吕志平, 李岩, 等. 基于格网的坐标转换方法[J]. 信息工程大学学报, 2010(2): 166-169. |
| [3] |
施建平, 楼楠, 乔亚明, 等. 坐标转换格网文件格式分析及转换[J]. 测绘与空间地理信息, 2013(5): 199-202. DOI:10.3969/j.issn.1672-5867.2013.05.065 |
| [4] |
成英燕. 大尺度空间域下1980西安坐标系与WGS84坐标系转换方法研究[J]. 测绘通报, 2007(12): 5-8. DOI:10.3969/j.issn.0494-0911.2007.12.002 |
| [5] |
王文利, 程传录, 陈俊英. 常用坐标转换模型及其实用性研究[J]. 测绘地理信息, 2010, 35(5): 37-39. |
| [6] |
赵文, 刘邢巍, 袁鹏. 格网节点坐标初值对格网坐标转换精度的影响[J]. 测绘地理信息, 2015, 40(2): 40-43. |
| [7] |
唐敏炯. 相似变换模型在平面坐标系变换中的有效性分析[J]. 现代测绘, 2011(6): 13-15. DOI:10.3969/j.issn.1672-4097.2011.06.004 |
| [8] |
于庆波. 辽宁省基础地理信息数据坐标转换系统设计与实现[J]. 城市建设理论研究(电子版), 2015(10): 1 566-1 567. |
| [9] |
Stupovski B M, Crnjanski J V, Gvozdic D M. Application of Coordinate Transformation and Finite Differences Method in Numerical Modeling of Quantum Dash Band Structure[J]. Computer Physics Comnunication, 2011, 182(2): 289-298. DOI:10.1016/j.cpc.2010.09.014 |
| [10] |
李克恭. 格网法和参数法应用于CGCS 2000转换的比较[J]. 测绘与空间地理信息, 2011(5): 227-230. |
 2022, Vol. 47
2022, Vol. 47

