| 地球自转速度变化与全球气温变化的相关性研究 |
2. 武汉大学卫星导航定位技术研究中心, 湖北 武汉, 430079
2. GNSS Research Center, Wuhan University, Wuhan 430079, China
全球气温上升对生态环境、经济安全等诸多领域都有弊大于利的综合性影响。如丁一汇等[1]报道,目前中国的温度变化未超过气候自然变率范围,难以确认气温的变化是由人类活动造成。近年来人们认识到地球自转速度变化与全球气候变化的联系,但关于地球自转速度变化与气温变化相关性的研究较少,暂无明确成果。本文针对地球自转变化数据和气温数据分别进行简单的数据建模与检验,并根据相关性分析与显著性分析法进行二者相关性与精度验证分析,再利用回归方程法建立回归方程,尝试在误差精度较小的时间范围进行未来的全球温度变化预测,并总结分析。
1 地球自转速度变化分析地球的自转速度是在不断发生变化的,简要可将其分为长期变化与短期变化:据Kurtlambeck、Scrutton和Pannella的研究表明[2-4],地球自转速度有逐渐减弱的长期减慢趋势。研究发现主要有以下叠加原因:潮汐摩擦[5]、重力分异[6]和其他因素[7]。地球自转速度的短期变化上,郑大伟等[8]以及罗时芳等[9]的研究证明,存在十年起伏周期性变化,同时地球自转速度存在季节性变化以及有短期不规则日变化[10]。根据张素琴[11]、钱维宏[12]的研究数据,可推测地球自转变化与气温变化或由其引发的自然灾害具有一定的同步性。
地球自转时间LOD(length of day, 表示地球日长时间实际值)与24 h差值,可表征地球自转速率的变化,是UT1-UTC对时间的一阶导数(世界时UT1, universal time;协调世界时UTC, universal time coordinated)。地球自转参数ERP(earth rotation parameter)包括了UT1-UTC。目前有许多可获取高精度ERP参数的空间大地测量技术[13],但都是事后处理出的数据,缺少时效性,故采用参数预报的方法来弥补该缺陷。国际上有大量地球自转参数预报模型[14-16],其中LS、LS+AR模型为最常用的模型。
2 全球气温变化与数学建模全球温度整体为加速趋势[17]的普遍回升,且并非呈直线趋势上升,是在时间上呈波动性增长,在空间上有明显的地域差异。
2.1 数学建模简单分析获取的温度数据,根据数据图像性质分析,傅里叶(Fourier)拟合与高斯(Gauss)拟合较为适合全球气温随时间变化的规律。以1962-2010年的年均气温数据为例,利用Matlab软件分别对其进行Fourier拟合与Gauss拟合。
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Fourie}}{{\rm{r}}_5}\left( x \right) = {\rm{ }}\\ {a_0} + {a_1} \cdot {\rm{cos}}\left( {x \cdot w} \right) + {b_1} \cdot {\rm{sin}}\left( {x \cdot w} \right) + \\ \cdot \cdot \cdot + {a_5} \cdot {\rm{cos}}\left( {5 \cdot x \cdot w} \right) + {b_5} \cdot {\rm{sin}}\left( {5 \cdot x \cdot w} \right) \end{array} $ | (1) |
其中,
| $ \left\{ \begin{array}{l} {a_0} = 8.871, w = 0.147{\rm{ }}9, {a_1} = 0.269{\rm{ }}4\\ {b_1} = - 0.122{\rm{ }}6, {a_2} = 0.106{\rm{ }}7, {b_2} = 0.072{\rm{ }}07\\ {a_3} = 0.020{\rm{ }}6, {\rm{ }}{b_3} = 0.072{\rm{ }}07, {a_4} = - 0.058{\rm{ }}03\\ {b_4} = 0.080{\rm{ }}88, {a_5} = 0.054{\rm{ }}35, {b_5} = 0.038{\rm{ }}38 \end{array} \right. $ |
拟合结果为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} {\rm{SSE}} = 0.924\\ {\rm{RMSE}} = 0.181{\rm{ }}7\\ {R^2} = 0.736{\rm{ }}3 \end{array} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Fourie}}{{\rm{r}}_6}\left( x \right) = \\ \;\;{a_0} + {a_1} \cdot {\rm{cos}}\left( {x \cdot w} \right) + {b_1} \cdot {\rm{sin}}\left( {x \cdot w} \right) + \\ \ldots + {a_6} \cdot {\rm{cos}}\left( {6 \cdot x \cdot w} \right) + {b_6} \cdot {\rm{sin}}\left( {6 \cdot x \cdot w} \right) \end{array} $ | (2) |
其中,
| $ \left\{ \begin{array}{l} {a_0} = 8.918, w = 0.138{\rm{ }}9, {a_1} = 0.215{\rm{ }}4\\ {b_1} = 0.258{\rm{ }}7, {a_2} = - 0.164{\rm{ }}4, {b_2} = 0.000{\rm{ }}109{\rm{ }}3\\ {a_3} = 0.039{\rm{ }}7, {b_3} = - 0.087{\rm{ }}34, {a_4} = 0.064{\rm{ }}8\\ {b_4} = 0.059{\rm{ }}02, {a_5} = 0.015{\rm{ }}54, {b_5} = - 0.062{\rm{ }}37\\ {a_6} = 0.035{\rm{ }}71, {b_6} = - 0.085{\rm{ }}08 \end{array} \right. $ |
拟合结果为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} {\rm{SSE}} = 0.833{\rm{ }}2\\ {\rm{RMSE}} = 0.179\\ {R^2} = 0.762{\rm{ }}2 \end{array} \right.\\ {\rm{Gaus}}{{\rm{s}}_5} = {a_1} \cdot {\rm{exp}}\left( { - {{\left( {\frac{{x - {b_1}}}{{{c_1}}}} \right)}^{^2}}} \right) + \\ \;\;\;\;\; \cdot \cdot \cdot + {a_5} \cdot {\rm{exp}}\left( { - {{\left( {\frac{{x - {b_5}}}{{{c_5}}}} \right)}^{^2}}} \right) \end{array} $ | (3) |
其中,
| $ \left\{ \begin{array}{l} {a_1} = 8.899, {a_2} = 0.869, {a_3} = 2.87\\ {a_4} = 157, {a_5} = 0.823{\rm{ }}3, {b_1} = 2{\rm{ }}001\\ {b_2} = 1{\rm{ }}981, {b_3} = 1{\rm{ }}973, {b_4} = 1{\rm{ }}859\\ {b_5} = 1{\rm{ }}988, {c_1} = 24.21, {c_2} = 3.701\\ {c_3} = 11.18, {c_4} = 58.25, {c_5} = 3.375 \end{array} \right. $ |
拟合结果为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} {\rm{SSE}} = 0.855{\rm{ }}5\\ {\rm{RMSE}} = 0.185\\ {R^2} = 0.755{\rm{ }}8 \end{array} \right.\\ {\rm{Gaus}}{{\rm{s}}_6} = {a_1} \cdot {\rm{exp}}\left( { - {{\left( {\frac{{x - {b_1}}}{{{c_1}}}} \right)}^2}} \right) + \\ \;\;\;\;\; \cdot \cdot \cdot + {a_6} \cdot {\rm{exp}}\left( { - {{\left( {\frac{{x - {b_6}}}{{{c_6}}}} \right)}^2}} \right) \end{array} $ | (4) |
其中,
| $ \left\{ \begin{array}{l} {a_1} = 9.34, {a_2} = 2.649, {a_3} = 0.937\\ {a_4} = 3.52, {a_5} = 1.64, {a_6} = 6.164\\ {b_1} = 2{\rm{ }}000, {b_2} = 1{\rm{ }}980, {b_3} = 1{\rm{ }}988\\ {b_5} = 1{\rm{ }}962, {b_6} = 1{\rm{ }}962, {c_1} = 28\\ {c_2} = 5.243, {c_3} = 3.351, {c_4} = 5.368\\ {c_5} = 1.13, {c_6} = 6.629 \end{array} \right. $ |
拟合结果为:
| $ \left\{ \begin{array}{l} {\rm{SSE}} = 0.766{\rm{ }}6\\ {\rm{RMSE}} = 0.186{\rm{ }}7\\ {R^2} = 0.781{\rm{ }}2 \end{array} \right. $ |
式(1)、式(2)(简称F5、F6)与式(3)、式(4)(简称G5、G6),为选取的与1962-2001年平均温度数据最优的傅里叶拟合与高斯拟合公式。其中,下标n为项数,a、b、c、w为未知参数;SSE、RMSE、R2为拟合函数与数据拟合的健康程度指标。SSE为和方差,RMSE为均方根误差,R2为确定系数,正常取值范围[0, 1]。SSE接近0,R2接近0,Rsquare接近1,说明模型对数据的拟合程度越高。根据健康程度指标对比,知同一类型的数学模型对比,拟合参数项级数越高,拟合效果越好;相异类型、相同项数对比,Gauss比Fourier的拟合效果更好。
 |
| 图 1 数学建模流程 Fig.1 Mathematical Modeling Process |
2.2 模型温度预测分析
以建立的F5、F6、G5、G6 4个拟合函数进行短期温度预测,并与实际温度数据对比分析。图 2(a)为拟合模型预测温度与实际真实温度数值对比图;图 2(b)为预测温度与实际温度差值柱状图。各数据对比可得,同类型的拟合函数模型,拟合程度更高,短期温度预测效果更好;拟合模型的类型对温度预测也有影响,且比拟合程度对数据预测的影响大,故选择正确的模型类别对于数据预测非常重要。
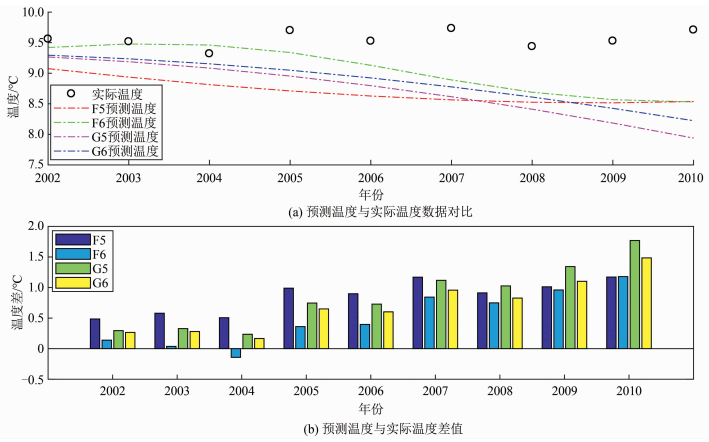 |
| 图 2 模型预测与实际数据对比 Fig.2 Model Prediction Versus Actual Data |
选短期预测效果更好的G6、F6进行长期的温度预测,以1750-2010年为例预测并与实际温度进行对比分析。
图 3蓝点为年实际温度,红线为F6拟合模型,黄线为G6拟合模型。无论是F6还是G6,长期温度预测结果和实际数据相比有非常大的误差,判定无法进行长期的温度预测。
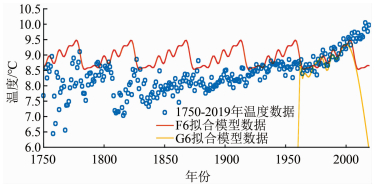 |
| 图 3 1750-2010年拟合模型预测与实际数据对比 Fig.3 Fitting Model Prediction for 1750-2010 Compared with Actual Data |
3 地球自转速度变化与全球气温变化的数据分析
将1962-2010年的时间分辨率为1 d的LOD数据进行年相加处理,得到49组地球每年实际日长时间与理论年长的差值数据,称处理后LOD为YearSum_LOD数据(简称YSLOD)。
| $ \begin{array}{l} {\rm{YSLOD\_Gaus}}{{\rm{s}}_5} = {a_1} \cdot {\rm{exp}}\left( { - {{\left( {\frac{{x - {b_1}}}{{{c_1}}}} \right)}^2}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\; \cdot \cdot \cdot + {a_5} \cdot {\rm{exp}}\left( { - {{\left( {\frac{{x - {b_5}}}{{{c_5}}}} \right)}^2}} \right) \end{array} $ | (5) |
其中,
| $ \left\{ \begin{array}{l} {a_1} = 0.42, {a_2} = 0.947, {a_3} = 0.897\\ {a_4} = 0.787, {a_5} = 0.381, {b_1} = 1{\rm{ }}972\\ {b_2} = 1{\rm{ }}978, {b_3} = 1{\rm{ }}967, {b_4} = 1{\rm{ }}993\\ {b_5} = 1{\rm{ }}983, {c_1} = 2.43, {c_2} = 4.347\\ {c_3} = 6.552, {c_4} = 8.346, {c_5} = 1.89 \end{array} \right. $ |
式(5)为YSLOD数据的G5函数模型建立。选取式(4)G6拟合为全球平均年气温拟合模型进行研究;按照数学建模方案步骤建模,再分别选取1962-2010年的全球平均年高温、全球平均年低温数据进行数学建模,为式(6)(H_G6)式(7)(L_G6)。
| $ \begin{array}{l} {\rm{H\_Temp\_Gaus}}{{\rm{s}}_6} = {a_1} \cdot {\rm{exp}}\left( { - {{\left( {\frac{{x - {b_1}}}{{{c_1}}}} \right)}^{^2}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\; \cdot \cdot \cdot + {a_6} \cdot {\rm{exp}}\left( { - {{\left( {\frac{{x - {b_6}}}{{{c_6}}}} \right)}^{^2}}} \right) \end{array} $ | (6) |
其中,
| $ \left\{ \begin{array}{l} {a_1} = 15.52, {b_1} = 2{\rm{ }}010, {c_1} = 55.45, {a_2} = 0.553{\rm{ }}2\\ {b_2} = 1{\rm{ }}988, {c_2} = 2.892, {a_3} = 11.65, {b_3} = 1{\rm{ }}940\\ {c_3} = 32.8, {a_4} = 0.381{\rm{ }}4, {b_4} = 1{\rm{ }}977, {c_4} = 0.307\\ {a_5} = 0.467{\rm{ }}2, {b_5} = 1{\rm{ }}972, {c_5} = 4.871, \\ {a_6} = 0.763{\rm{ }}9, {b_6} = 1{\rm{ }}981, {c_6} = 2.864 \end{array} \right. $ |
拟合结果为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} {\rm{SSE}} = 0.989{\rm{ }}5\\ {\rm{RMSE}} = 0.178{\rm{ }}7\\ {R^2} = 0.865{\rm{ }}3 \end{array} \right.\\ {\rm{L\_Temp\_Gaus}}{{\rm{s}}_6} = {a_1} \cdot {\rm{exp}}\left( { - {{\left( {\frac{{x - {b_1}}}{{{c_1}}}} \right)}^2}} \right) + \\ \;\;\;\;\;\;\;\;\; \cdot \cdot \cdot + {a_6} \cdot {\rm{exp}}\left( { - {{\left( {\frac{{x - {b_6}}}{{{c_6}}}} \right)}^2}} \right) \end{array} $ | (7) |
其中,
| $ \left\{ \begin{array}{l} {a_1} = 3.754, {b_1} = 2{\rm{ }}006, {c_1} = 15.66\\ {a_2} = 0.697{\rm{ }}3, {b_2} = 1{\rm{ }}996, {c_2} = 3.813\\ {a_3} = 1.734, {b_3} = 1{\rm{ }}989, {c_3} = 4.799\\ {a_4} = 1.034, {b_4} = 1{\rm{ }}982, {c_4} = 3.685\\ {a_5} = 1.678, {b_5} = 1{\rm{ }}975, {c_5} = 10.13\\ {a_6} = 1.322, {b_6} = 982.1, {c_6} = 174.5 \end{array} \right. $ |
拟合结果为:
| $ \left\{ \begin{array}{l} {\rm{SSE}} = 0.983{\rm{ }}7\\ {\rm{RMSE}} = 0.178{\rm{ }}1\\ {R^2} = 0.861{\rm{ }}7 \end{array} \right. $ |
以YSLOD为x轴,温度数据(年均温/高温/低温)为y轴,做出对应年的散点图,发现各温度都与YSLOD呈线性反比趋势。相关系数R用于数值与数值之间的关联性分析,根据计算相关系数R,判断数据的相关性与否与强弱,且R>0呈正相关;R < 0呈反相关。
解出全球年平均气温、高温、低温都与YSLOD有较强反相关性,即地球自转速度年变化与全球温度呈正相关。
为确定结论进行相关系数R与ρ的显著性水平分析,证明二者之间差异不显著。提出假设:H0:总体的相关系数ρ=0(即假设总体上气温与自转速度变化无相关性);H1:总体的相关系数ρ≠0。建立R的显著性分析T统计量:
| $ T = \frac{{R\sqrt {n - 2} }}{{\sqrt {1 - {R^2}} }} \sim t\left( {n - 2} \right) $ | (8) |
式中,R是相关系数;n是样本量。设置0.01、0.05为检验水准,按式(8)求解地球自转速度变化数据与各温度数据R的T统计量,进行显著性分析。求解出各T统计量,查找t分布界值表,获得临界值tα,并有当
如图 4所示为自由度为47的t分布与各T统计量对应数据值,以及检验水准对应的临界值。发现都有T <
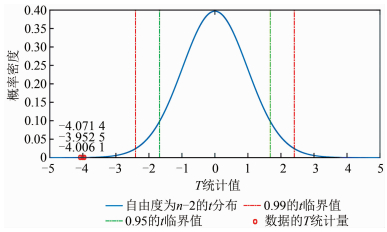 |
| 图 4 自由度为n-2的t分布与各T统计量对比 Fig.4 t Distribution of n-2 Degrees of Freedom Each T Statistic |
3.2 拟合模型相关性分析
本文选取式(5)为地球自转速度变化拟合模型,式(4)(G6)为全球年均温拟合模型,式(6)(H_G6)和式(7)(L_G6)为高温模型和低温模型,进行拟合模型数据相关性分析。
通过拟合模型数据绘制的散点图,判断年平均温度与年均高温与YSLOD的线性相关性较高,并根据拟合模型间的相关系数,知有较强的相关性,再进行显著性分析,求解各自相关系数的T统计量,进行显著性分析,证明地球自转速度与全球气温的确呈正相关。
3.3 温度预测及分析 3.3.1 实际数据预测温度分析1) 实际数据的线性回归拟合。回归分析法[19-21]是一种分析变量相关关系的统计方法。设实际地球自转速度年变化参数为自变量,实际全球年温度为因变量,利用回归分析法,建立线性回归方程式(9)、式(10)和式(11)。
| $ \left\{ \begin{array}{l} {\rm{Temp}} = 9.636 + \left( { - 0.976{\rm{ }}78} \right) \cdot {\rm{YSLOD}}\\ {R^2} = 0.576{\rm{ }}13;F = 63.883{\rm{ }}6;P = 0 \end{array} \right. $ | (9) |
| $ \left\{ \begin{array}{l} H\_{\rm{Temp}} = 15.404{\rm{ }}3 + \left( { - 1.015{\rm{ }}1} \right) \cdot {\rm{YSLOD}}\\ {R^2} = 0.610{\rm{ }}4;F = 73.637{\rm{ }}1;P = 0 \end{array} \right. $ | (10) |
| $ \left\{ \begin{array}{l} L\_{\rm{Temp}} = 3.960{\rm{ }}8 + \left( { - 0.990{\rm{ }}1} \right) \cdot {\rm{YSLOD}}\\ {R^2} = 0.599{\rm{ }}6;F = 70.381{\rm{ }}3;P = 0 \end{array} \right. $ | (11) |
式中,R2为相关系数,F为F检验的统计量,P为F对应概率。由式(9)~式(11)可知整体拟合效果都较好。
2) 实际回归方程的YSLOD_G5温度预测。利用拟合模型式(5)预测2011-2019年的地球自转速度年变化,并视其为自变量,分别代入式(9)、式(10)和式(11),对2011-2019年的全球气温进行预测。
图 5(a)为预测的地球自转速度年变化数据,图 5(b)、图 5(c)和图 5(d)为温度预测数据与实际数据对比图,发现预测效果都不太好;图 5(e)为每年预测温度与实际温度的差值变化图,发现随着时间的增加,差值呈波动性增加。
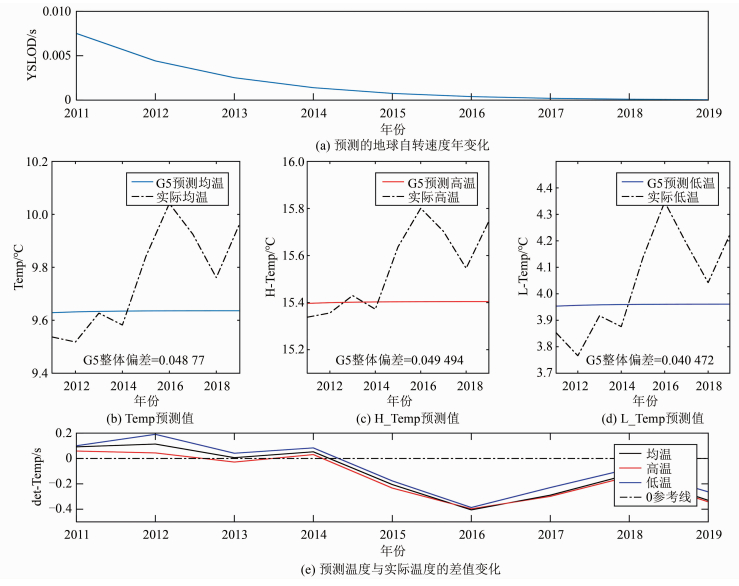 |
| 图 5 实际数据回归方程G5温度预测结果分析 Fig.5 G5 Temperature Prediction Results and Analysis of Linear Regression Equation of Actual Data |
3) 线性回归方程的YSLOD_F5温度预测。为判断温度预测过程中,预测的地球自转速度年变化数据,对最终温度预测的影响,更换自变量。
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;{\rm{YSLOD}}\_{\rm{Fourie}}{{\rm{r}}_5} = \\ \;\;{a_0} + {a_1} \cdot {\rm{cos}}\left( {x \cdot w} \right) + {b_1} \cdot {\rm{sin}}\left( {x \cdot w} \right) + \\ \cdot \cdot \cdot + {a_5} \cdot {\rm{cos}}\left( {5 \cdot x \cdot w} \right) + {b_5} \cdot {\rm{sin}}\left( {5 \cdot x \cdot w} \right) \end{array} $ | (12) |
其中,
| $ \left\{ \begin{array}{l} w = 0.103{\rm{ }}4, {a_0} = 0.549{\rm{ }}2, {a_1} = - 0.382{\rm{ }}9\\ {b_1} = - 0.177{\rm{ }}5, {a_2} = 0.113{\rm{ }}8, {b_2} = - 0.160{\rm{ }}6\\ {a_3} = - 0.061{\rm{ }}88, {b_3} = 0.081{\rm{ }}17, {a_4} = - 0.042{\rm{ }}99\\ {b_4} = 0.135{\rm{ }}9, {a_5} = 0.011{\rm{ }}23, {b_5} = 0.041{\rm{ }}32 \end{array} \right. $ |
式(12)为1962-2010年的地球自转速度年变化数据建立的新拟合模型。利用式(12)预测2011-2019年的自转速度年变化数据YSLOD_F5,并为自变量代入式(9)、式(10) 和式(11)进行气温预测,再与YSLOD_G5预测结果对比分析。
表 1为YSLOD_G5与此次实验预测结果偏差程度对比。二者有相同线性回归方程,而此次试验结果整体预测效果更好。
| 表 1 YSLOD_G5与YSLOD_F5温度预测误差对比 Tab.1 Comparison of Temperature Prediction Errors Between YSLOD_G5 and YSLOD_F5 |
 |
表 2为式(5)、式(12)拟合模型建立过程中拟合程度数据对比,知YSLOD_F5的拟合效果更好,又因模型类别比拟合效果影响更大,推测在相同回归方程下,地球自转速度年变化拟合模型质量越高,全球温度预测效果越好。
| 表 2 YSLOD_G5/F5对自转速度年变化的拟合程度 Tab.2 Fitting Degree of YSLOD_G5/F5 to Annual Variation of Earth's Rotation Velocity |
 |
3.3.2 拟合数据预测温度分析
1) 拟合模型数据的线性回归拟合。设地球自转速度年变化拟合模型式(5)所求1962-2010年数据为自变量,全球年气温的拟合模型式(4)(G6)、式(6)(H_G6)和式(7)(L_G6)为因变量,建线性回归方程式(13)、式(14)和式(15)。
| $ \left\{ \begin{array}{l} {\rm{FitTemp}} = 9.601 + \left( { - 0.947{\rm{ }}05} \right) \cdot {\rm{FitYSLOD}}\\ {R^2} = 0.791{\rm{ }}99;F = 178.945{\rm{ }}3;P = 0 \end{array} \right. $ | (13) |
| $ \left\{ \begin{array}{l} {\rm{FitH\_Temp}} = {\rm{ }}15.421{\rm{ }}3 + \left( { - 0.973{\rm{ }}89} \right) \cdot {\rm{FitYSLOD}}\\ {R^2} = 0.790{\rm{ }}53;F = 177.374;P = 0 \end{array} \right. $ | (14) |
| $ \left\{ \begin{array}{l} {\rm{FitL\_Temp}} = {\rm{ }}3.939{\rm{ }}8 + \left( { - 0.911{\rm{ }}85} \right) \cdot {\rm{FitYSLOD}}\\ {R^2} = 0.591{\rm{ }}39;F = 68.024{\rm{ }}5;P = 0 \end{array} \right. $ | (15) |
式(13)、式(14)和式(15)中的回归系数都为负数,根据标注R2数据可知FitTemp回归模型最准确,由F和P知三者拟合效果都较好。F检验的相同,可知此次实验拟合模型求解的均温、高温数据在方程建立过程中拟合效果更好。
2) 拟合模型数据线性回归的G5温度预测。利用拟合模型式(5)预测2011-2019年的地球自转速度年变化,并分别代入式(13)、式(14)和式(15),对2011-2019年的全球气温按实际数据线性回归方程的YSLOD_G5温度预测模式预测。发现温度预测效果与拟合效果优劣不符,推测将数据拟合成模型后建立的线性回归方程,虽然提高回归方程建立的拟合效果,却无法提高最终温度预测效果;误差主要由输入的自转速度变化本身的误差累积特点引起,推测利用地球自转速度变化来进行预测温度实验时,要想提升温度预测精度,主要需要建立一个优化的地球自转速度变化预测模型。
4 结束语本文实验证明,直接利用温度拟合模型可进行短期温度预测,无法进行较长期的温度预测;地球自转速度变化与全球温度变化的确存在强正相关性,高温相关性最强;建立的线性回归公式进行全球年均温度预测,由于输入的地球自转速度年变化预测本身带有的误差累积特点,预测精度有随时间增加趋势;根据表 2判断,利用地球自转速度变化与全球年均气温拟合模型建立线性回归方程,比利用原始数据建立线性回归方程的拟合效果程度高了约1~1.5倍;预测自转速度变化的模型的拟合程度与类别,对最终温度预测都有影响,地球自转速度变化拟合模型的质量对全球温度的预测效果影响最大,研究一个高质量的地球自转速度变化或预测模型,是提高温度预测的首要任务。
致谢: 感谢IERS和伯克利地球组织提供的观测数据。
| [1] |
丁一汇, 戴晓苏. 中国近百年来的温度变化[J]. 气象, 1994, 20(12): 19-26. DOI:10.7519/j.issn.1000-0526.1994.12.008 |
| [2] |
Kurtlambeck. The Earth's Variable Rotation[M]. England: Cambridge University Press, 1980.
|
| [3] |
Scrutton C T. Periodic Growth Features in Fossil Organisms and the Length of the Day and Month[M]. Berlin: Springer Berlin Heidelberg, 1978.
|
| [4] |
Pannella G. Paleontological Clocks and the History of the Earth's Rotation[M]. London: John Wiley, 1975: 253-284.
|
| [5] |
Stephenson F R. Historical Eclipses and Earth's Rotation[M]. England: Cambridge University Press, 1997.
|
| [6] |
杨冬红, 杨学祥. 地球自转速度变化规律的研究和计算模型[J]. 地球物理学进展, 2013, 28(01): 58-70. |
| [7] |
Wu B, Schuh H, Peng B. New Treatment of Tidal Braking of Earth Rotation[J]. Journal of Geodynamics, 2003, 36(4): 515-521. DOI:10.1016/S0264-3707(03)00063-2 |
| [8] |
郑大伟, 周永宏. 地球自转变化与全球地震活动关系的研究[J]. 地震学报, 1995(1): 25-30. |
| [9] |
罗时芳, 梁世光, 叶叔华, 等. 地球自转速率变化的周期分析[J]. 天文学报, 1974, 15(1): 79-85. |
| [10] |
顾震年. 太阳活动对地表气候和地球自转的影响[J]. 天文学进展, 1991, 9(1): 51-59. |
| [11] |
张素琴. 地球自转与东北地区夏季温度变化[J]. 应用气象学报, 2000, 11(4): 484-490. DOI:10.3969/j.issn.1001-7313.2000.04.012 |
| [12] |
钱维宏. 长期天气变化与地球自转速度的若干关系[J]. 地理学报, 1988(1): 60-66. DOI:10.3321/j.issn:0375-5444.1988.01.007 |
| [13] |
王志文. GNSS解算地球自转参数及预报模型研究[D]. 徐州: 中国矿业大学, 2018: 1-120
|
| [14] |
李斐, 邵先远, 曲春凯, 等. 利用2006-2015年VLBI数据进行地球定向参数解算与分析[J]. 武汉大学学报·信息科学版, 2019, 44(11): 1. |
| [15] |
许雪晴, 周永宏. 地球定向参数高精度预报方法研究[J]. 飞行器测控学报, 2010, 29(2): 70-76. |
| [16] |
秦大河, 罗勇. 全球气候变化的原因和未来变化趋势[J]. 科学对社会的影响, 2008(2): 16-21. DOI:10.3969/j.issn.2095-1949.2008.02.004 |
| [17] |
凌三力, 王甫红, 张万威. 风云三号C卫星星载GPS/BDS实时定轨分析[J]. 测绘地理信息, 2021, 46(3): 17-20. |
| [18] |
柏露, 姚宜斌, 雷祥旭, 等. 近40年青藏高原地区地表温度的年际及季节性变化特征分析[J]. 测绘地理信息, 2018, 43(2): 15-18. |
| [19] |
张胜黎. 收集数据建立函数模型——以"龙井问茶"为例[J]. 中学教研: 数学, 2020(1): 26-28. |
| [20] |
马开玉. 现代应用统计学[M]. 北京: 气象出版社, 2004.
|
| [21] |
郑健. 经验模态分解中IMF分量判定准则方法实验研究[J]. 测绘地理信息, 2021, 46(3): 33-37. |
 2021, Vol. 46
2021, Vol. 46


