| 光学水准尺图像数字化处理及其自动化读数实现 |
几何水准测量是利用仪器建立一条水平视线,然后读取视线两端的水准标尺刻划,由刻划读数差计算出标尺立尺点的高差[1],从而由一点的已知高程,推算另一点的高程。目前应用广泛的水准仪分为光学水准仪和数字水准仪。数字水准仪虽然具有读数客观、精度高、速度快、效率高、操作简单等优点[2],但成本较高。因此在小型工程中依旧采用光学水准仪进行高程测量,人为读数效率较低且易受主观误差的影响。国内外对于数字水准仪的研究颇多,多集中于条码水准尺的编码、解码[3],但基于光学水准仪和普通“E”形水准尺测量进行数字化自动读数的研究甚少。本文利用从光学水准仪目镜处获取的图像,结合图像处理相关技术,自动获取光学水准仪三丝读数,实现了光学水准仪的自动读数,可提高工作效率,避免人为读数误差的影响。
1 水准尺的图像处理和数字化 1.1 水准尺图像的预处理利用安装在光学水准仪目镜处的摄像头获取水准尺的影像。图像颜色像素值采用三属性值(RGB)表示[4],将获取的彩色图像在通道上取平均得到灰度图像[5],同时获得相应灰度图像的灰度矩阵
实现水准尺图像的数字化需要经过背景分离、区分水准尺红黑面、水准尺二值化、水准尺缩放、水准尺匹配处理,最终获得相应的匹配偏移系数,计算出正确的读数。
1) 列间灰度单差算法实现水准尺背景分离
对预处理获得的灰度矩阵Im×n(m代表行数,n代表列数)的每列进行累加并求取平均值获得新的矩阵Pn,即:
| $ \mathit{\boldsymbol{P}}\left( j \right) = \sum\limits_{i = 0}^{i = m - 1} {\mathit{\boldsymbol{I}}\left( {i, j} \right){\rm{/}}m} $ | (1) |
将矩阵Pn进行列间单差,获得单差后的矩阵P_n,其中:
| $ \mathit{\boldsymbol{P}}\_\left( 0 \right) = 0 $ | (2) |
| $ \mathit{\boldsymbol{P}}\_\left( i \right) = \left| {\mathit{\boldsymbol{P}}\left( i \right) - \mathit{\boldsymbol{P}}\left( {i - 1} \right)} \right|, i \in \left( {1, n - 1} \right) $ | (3) |
一般而言,矩阵P_中前8大值对应的下标中应包含有水准尺边界对应的下标,从而保证水准尺边界位置搜寻的正确性。因此,选取其前8大值,并存储相应的下标、计算的列间单差值,以及其8大值间下标互差之和与最大下标差相减的值。以8大值间下标互差之和与最大下标差相减的值的平方倒数作为权值,对相应的单差值进行处理。即在矩阵select8×3中,select(i, 0)=第(i+1)大单差值的下标; select(i, 1)=第(i+1)大的单差值; select(i, 2)=第(i+1)大的单差值与其他单差下标互差之和与最大下标差之差。
权值矩阵P8中:
| $ \mathit{\boldsymbol{P}}\left( i \right) = \frac{1}{{{\rm{select}}{{\left( {i, 2} \right)}^2}}} $ | (4) |
可知8大值中聚集的部分,其对应的权值会比其他部分大,以此实现聚类者单差值减少较慢,而非聚类部分单差值减小较快。而单差位置的聚集区为水准尺所在区域,这是由于水准尺特殊的尺面字符分布造成的。因此非聚类的单差值可视为干扰信息,依此不断削弱干扰的单差值,即:
| $ {\rm{select}}\left( {i, 1} \right) = {\rm{select}}\left( {i, 1} \right) \times \mathit{\boldsymbol{P}}\left( i \right) $ | (5) |
设置一定阈值,提取出超过阈值的聚类单差值所对应下标的最大和最小值,即得出下标范围,此范围边界即为水准尺的分割边界。依据此边界最终实现水准尺的背景分离。
图 1(a)给出了图像每列的列间单差值并绘成了竖线图;图 1(b)给出了图 1(a)中列间单差值的前8大值;图 1(c)给出了图 1(b)中前8大列间单差值经过聚类处理后,聚集在一起的列间单差值减小程度远远小于非聚类单差值的变化。图 2给出了在图 1(c)基础上通过设置阈值寻找出水准尺在图像列方向上的边界。
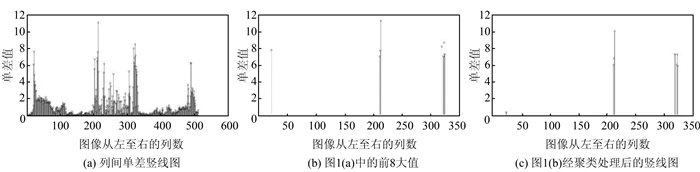 |
| 图 1 灰度值矩阵列间单差竖线图 Fig.1 Distribution of the Single Difference Between the Adjacent Columns of the Gray Value Matrix |
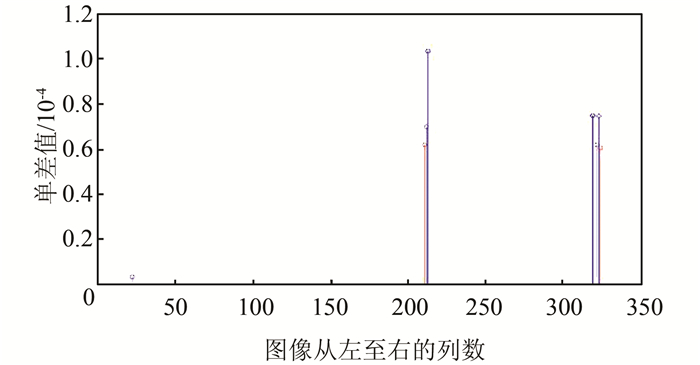 |
| 图 2 水准尺分离的灰度值矩阵列间单差界线位置 Fig.2 Boundary of the Optical Levelling Staff in the Single Difference Between the Adjacent Columns of the Gray Value Matrix |
2) 通道间单差算法区分红黑面
以一个通道作为基准,与其他两个通道作差值,即ΔRG=R-G,ΔRB=R-B,理想情况下当为黑面时,绝大部分ΔRG与ΔRB的平均值都将接近0,当其为红面时有相当大部分接近于255。
3) 分区Otsu实现水准尺二值化
黑白图像是二值灰度图像,其两个灰度值分别为0和255[6]。利用分区Otsu实现水准尺灰度图的二值化,可消除图像中阴影对于匹配的干扰,凸显出尺面的字符信息。
Otsu算法原理的基本思想是预先取一个初始阈值t对图像进行分割,将原图像分割成两部分C1和C2,分别为像素灰度值大于等于t的部分和小于t的部分,然后对这两部分分别计算类间方差σB2和类内方差σA2,最终找出图像最佳阈值t,即使两个方差比σB2/σA2达到最大时t的值[7]。
在实际图片采集过程中,拍摄图片的背景光照有时是不均匀的,这样就对图片的二值化造成困难[8],而对于一定大小区域而言光照分布大致均匀。均值二值化和整体Otsu等常用的单阈值算法,在光照不均匀下表现不佳。因此本文将整幅图像分割为若干个子图像,对每个子图像分别进行Otsu处理,即分区Otsu处理,可以改善光照分布不均匀图像二值化效果差的情况。分区的大小一般选为整幅图像的1/6左右。
图 3(a)给出了分离的水准尺灰度图;图 3(b)给出了分离后灰度化的水准尺经均值二值化处理的效果,可以看出噪声较多,效果不太理想;图 3(c)给出了水准尺灰度图经整体Otsu处理的效果,噪声虽然较少,但有字符不清晰的问题存在,如字符“58”不太清晰;图 3(d)给出了灰度化水准尺分区Otsu处理的效果,处理后的图像噪声较少,而且字符比较清晰,效果较好。
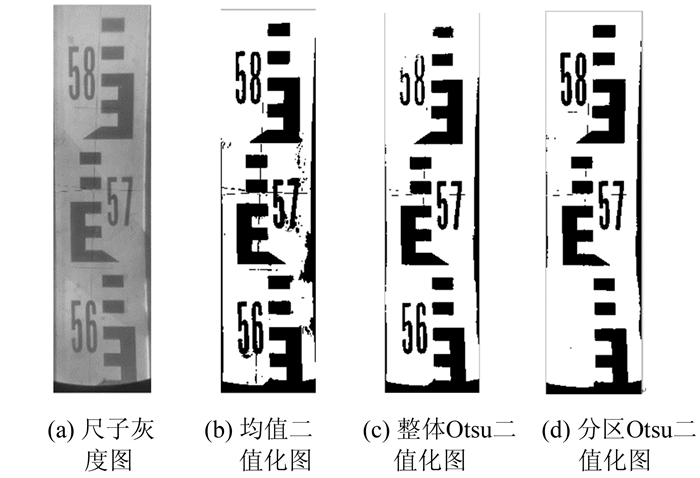 |
| 图 3 灰度尺经不同二值化方法处理后的图像 Fig.3 Images of the Gray Optical Levelling Staff by Different Binarization Methods |
4) 双线性插值实现二值化水准尺的缩放
二值化后的水准尺的宽度width_obj缩放后应与二值化数字模板水准尺的宽度width_temp相同,依此得出缩放系数r=
图 4给出了利用双线性插值进行缩放前后的水准尺图像,可以看出双线性插值实现的缩放较好的保留了缩放前图像的信息。
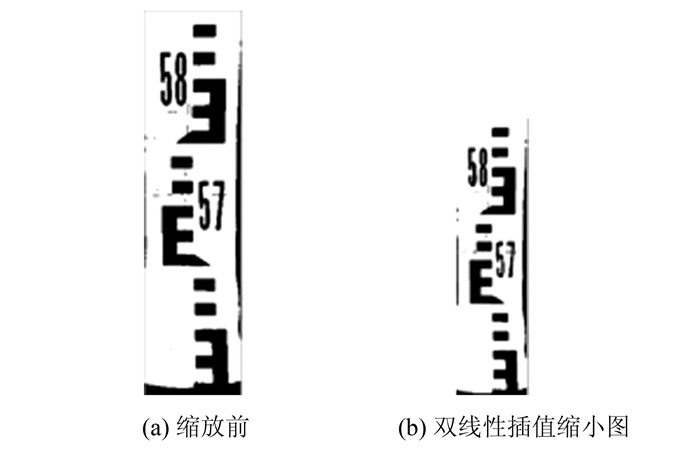 |
| 图 4 二值化水准尺缩放 Fig.4 Zoom Effect of the Binarization Optical Levelling Staff |
5) 金字塔匹配获取偏移系数
已有的影像匹配算法大致可以分为基于灰度的影像匹配和基于特征的影像匹配两类[10]。本文采用的金字塔匹配是基于灰度的影像匹配算法。
首先在大尺度图像上进行匹配,确定一个大概的匹配范围,然后缩小匹配尺度,依据确定的匹配范围进行匹配,进一步缩小匹配范围,直至最终实现要求精度的匹配,获得相应的偏移系数。
本文采用三级金字塔匹配,相比于直接的匹配,金字塔影像自下而上每一层的像素数都不断减少,这会大大减少计算量[11],运行速度有大幅提升,节省了时间,提高了程序整体的运行速度。
2 水准尺读数的获取及其精度评定 2.1 图像匹配获取水准尺读数由于加装在目镜处的摄影仪器位置是固定的,三丝在目镜中的相对位置也是固定不变的。因此拍摄的图片中三丝的位置始终保持不变。将目镜的背景设置为白墙,拍取图片后识别出三丝在图片竖直方向的位置。为了保证三丝在图片中竖直位置的精度,可以多次拍取图片,处理后进行均值处理。
在获取了三丝在图像中的相对位置后,将获取图像中的水准尺(图 5(b),a、b、c代表三丝在图中的位置)与模板水准尺图(图 5(a)),经过如图 5(c)所示的匹配后获得偏移系数,可以推知三丝在模板水准尺中的位置。由模板水准尺建立的位置和读数的对应关系得出三丝的读数。
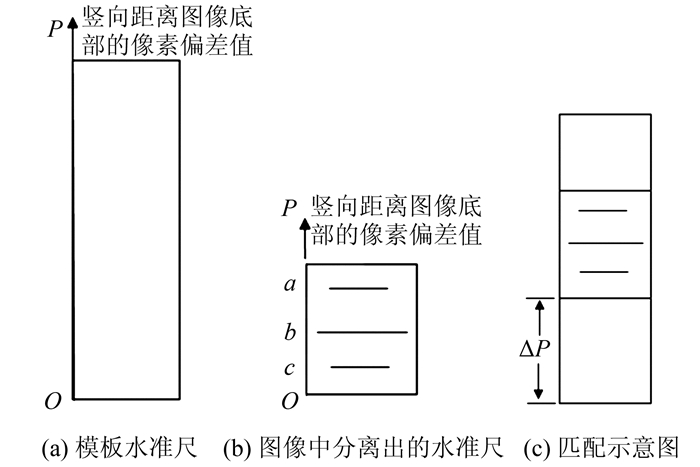 |
| 图 5 图像匹配获取三丝读数的原理 Fig.5 Principle of Obtaining Three Lines Readings by Image Matching |
由此得三丝在模板水准尺中的位置:上丝=a+ΔP,中丝=b+ΔP,下丝=c+ΔP,再由模板水准尺中的位置和读数形成的对应关系得出三丝的读数。
2.2 水准尺读数的精度评定以上丝为例进行分析说明,中、下丝类似。假设水准尺在3 m刻线间竖直方向的像素个数为m个,则每个像素对应的高度Δh(mm)=3 000/m。上丝在图像中的位置为a,偏移系数为ΔP,常数k,则上丝读数为:
| $ {\rm{u}}{{\rm{p}}_{{\rm{number}}}}{\rm{ = }}\left( {a + \Delta P + k} \right) \times \Delta h $ | (6) |
则有:
| $ \begin{array}{l} \Delta {\rm{u}}{{\rm{p}}_{{\rm{number}}}}{\rm{ = }}\frac{{3\;000\left( {\delta a + \delta \Delta P + \delta k} \right)}}{m} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{3\;000\left( {a + \Delta P + k} \right) \times \delta m}}{{{m^2}}} \end{array} $ | (7) |
式中,m与k可视为无误差,则δm=0,δk=0,则:
| $ \Delta {\rm{u}}{{\rm{p}}_{{\rm{number}}}}{\rm{ = }}\frac{{3\;000\left( {\delta a + \delta \Delta P} \right)}}{m} $ | (8) |
由此可知,δa、δΔP越小,即在图像中的位置误差越小,偏移系数误差越小;m越大,即模板水准尺的竖直分辨率越高,则获得的读数误差越小,读数的精度越高。
3 实例及数据分析 3.1 成本分析一整套电子水准测量设备价格一般在12 000元左右。一整套光学水准仪大概1 500元左右,本项目实现过程中需要加装一个CCD器件大概500元,因此整套设备2 000元左右。与电子水准设备的12 000元相比,本项目的整套设备成本较低,价格相当低廉。
3.2 精度和效率分析一般情况下,在程序实验过程中,δa与δΔP会有一到两个像素的误差,平均情况下则有,
| $ \Delta {\rm{u}}{{\rm{p}}_{{\rm{number}}}}{\rm{ = }}\frac{{6\;000}}{m}{\rm{mm}} $ |
则当数字模板水准尺竖直方向分辨率为12 000个像素时,则有:
| $ \Delta {\rm{u}}{{\rm{p}}_{{\rm{number}}}}{\rm{ = }}\frac{{6\;000}}{{12\;000}}{\rm{ = 0}}{\rm{.5}}\;{\rm{mm}} $ |
即读数误差为0.5 mm。而人眼读数误差一般为1~2 mm。因此读数精度会有所提高。此外通过实验得知自动读数的速度平均为850 ms/次,而人眼读数速度为2 s/次。因此读数的速度也比人眼读数快很多。
4 结束语本文结果表明,通过数字图像处理算法可以较好地处理光学水准仪目镜处获取的光学水准尺影像,并针对水准尺背景分离问题,提出了列间单差的算法。因此,通过加装在光学水准仪目镜处的摄像仪器获取图像,再利用本文给出的整套算法,可以快速有效的获得光学水准仪目镜处三丝的读数,实现光学水准仪的自动读数。克服了目前电子水准仪价格高昂、光学水准仪效率低下的缺点,以低成本有效地提高工作效率。同时避免了人为读数的误差,提高了读数的精度。此外若将一个测站的数据进行自动化处理,提升的效率将更加明显,这将是本文后续完善的方向。
| [1] |
陆优.数字水准仪原理及检测方法的研究[D].武汉: 武汉大学, 2004 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y630919
|
| [2] |
张志勇. 数字水准仪的原理特点及测量算法综述[J]. 大坝与安全, 2004(s1): 4-9. |
| [3] |
肖进丽, 李松, 胡克伟. 几种数字水准仪标尺的编码规则和读数原理比较[J]. 测绘通报, 2004(10): 57-59. DOI:10.3969/j.issn.0494-0911.2004.10.020 |
| [4] |
陆佳辉.基于数码相机的光谱颜色定量化和显示器复现[D].杭州: 杭州电子科技大学, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10336-1015549613.htm
|
| [5] |
何东健. 数字图像处理[M]. 第三版. 西安: 西安电子科技大学出版社, 2015.
|
| [6] |
刘玉红, 王志芳, 杨佳仪, 等. 彩色图像二值化算法及应用[J]. 中国医学物理学杂志, 2013, 30(1): 3873-3876. DOI:10.3969/j.issn.1005-202X.2013.01.009 |
| [7] |
陈思. 基于Otsu算法的车牌图像二值化及其Matlab实现[J]. 长春师范大学学报, 2012, 31(3): 33-35. DOI:10.3969/j.issn.1008-178X-B.2012.03.010 |
| [8] |
郭佳, 刘晓玉, 吴冰, 等. 一种光照不均匀图像的二值化方法[J]. 计算机应用与软件, 2014(3): 183-186. DOI:10.3969/j.issn.1000-386x.2014.03.048 |
| [9] |
王会鹏, 周利莉, 张杰. 一种基于区域的双三次图像插值算法[J]. 计算机工程, 2010, 36(19): 216-218. DOI:10.3969/j.issn.1000-3428.2010.19.076 |
| [10] |
陈慧颖, 刘进, 杨洁, 等. 基于ORB算法改进的影像匹配方法[J]. 测绘地理信息, 2015, 40(3): 31-34. |
| [11] |
陈敏.基于多尺度的图像特征提取与匹配研究[D].长沙: 中南大学, 2011 http://cdmd.cnki.com.cn/Article/CDMD-10533-1011176218.htm
|
 2019, Vol. 44
2019, Vol. 44

