| 面向配电网规划的地理接线图简化方法研究 |
2. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉,430079
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
配电网规划是电网建设中的一项重要工作,科学合理的规划是电网经济建设与可靠运行的关键因素[1]。配电网地理接线图是规划工作中必不可少的可视化数据,可以提供电力系统中发电厂、变电站以及物理杆塔等电力设施的地理位置和拓扑连接关系,是电力线路走向以及配电设施间相互连接关系最直观的体现。但基于配电网现状数据直接生成的地理接线图不适合直接用于配电网规划,以湖北省的高压配电网的规划为例,存在以下问题:①目前配电网现状数据主要依靠人工整理生成,数据质量问题较多;②现有配电网数据模型复杂,大量规划无关设备使得配电网网架的空间拓扑关系极为复杂,生成的地理接线图可视化效果较差,不利于规划人员决策。
近年来,随着国内外智能电网发展与信息平台建设推进,配电网可视化方法与技术受到愈来愈多的研究人员的密切关注,Rao等[2]结合美学标准总结图形生成的准则,并提出以拓扑图包含的所有边作为输入生成辐射状配电馈线图的方法;宋峰等[3]提出了一种基于航拍图像识别的电网地理接线图绘制方法;章坚民等[4]提出的以变电站为中心的配电网动态辐射状均匀接线图的的生成算法;刘行波等[5]针对传统的多用户地理接线图数据集成中存在的边界区域线路错位情况,提出一种面向规划的地理接线图线路自动定向与接边方法;刘志松等[6]针对传统抽稀算法无法识别配电网地理接线图中的特征点,提出一种面向电网规划的地理接线图自动抽稀方法。但是以上这些研究中都没有考虑空间位置约束,生成的图形或失去原有的相对空间关系,或位置误差过大。在配电网规划中,可视化图形的空间位置和拓扑关系同等重要,现有的方法无法解决配电网图形简化的诸多问题。
本文提出一种面向配电网规划的地理接线图简化方法,针对当前地理接线图存在的线路分布密集,难以区分,空间位置信息过于丰富,影响可视化效果等问题,将配电网地理接线图中代表配电网线路的线要素基于改进的道格拉斯-普克算法进行简化,提升其可视化效果,同时兼顾配电设施准确的空间位置和线路间清晰的拓扑关系。本文以湖北省鄂州市高压配电网网架数据作为简化实例进行研究。
1 配电网地理接线图简化方法配电网地理接线图的简化,涉及的对象为代表导线段、电缆段的线要素和代表杆塔的点要素,其中,点要素对站外地理接线图的可视化效果影响较小,而线要素由于交错连接,在图上显示密集甚至交叉重叠,严重影响地理接线图的可视化效果,因此,对配电网地理接线图简化实际上是对地理接线图中的线状要素的进行简化。
传统的道格拉斯-普克算法[7-10]是通用的线要素简化方法,对待简化曲线上的所有节点都采取一致的处理方法,即曲线点是否简化只取决于该点到对应直线的距离,或者该点对曲线形状的重要程度。但配电网由多条配电线路交错连接,呈网状结构,同时考虑到配电网特有的输电特性以及地理接线图成图规范,线路上的节点有的可以简化,有的必须保留。传统的道格拉斯-普克算法不能直接应用于配电网的地理接线图简化。
配电网中的节点代表杆塔,但是杆塔有多种类型,包括直线杆、耐张杆、转角杆、终端杆等,部分关键节点还会影响电网的拓扑结构和输电特性,比如T节点。本文将节点划分为两类:一类是可以被简化的节点,该类节点通常是对线路起着架空支撑和改变方向的作用;另一类是必须保留的节点,该类节点通常在配电网中对输电特性起到关键作用,如T节点或者挂载有关键设备的杆塔等。本文基于不同节点的重要程度,提出基于特征点的道格拉斯-普克算法,进而构建图形简化算法。
1.1 配电网Stroke划分策略配电网站外的图形结构是由导线段和电缆段构成,但是导线段与电缆段之间的连接关系复杂,呈网络结构,因而需对网络结构的配电网图形转化为Stroke集合。Stroke作为简化的基元,是最小的简化单位,通常由多个具有关联性的导线段或电缆段组成,Stroke的特点是高内聚低耦合,即Stroke的内部导线段或电缆段集合具有高关联度,而与Stroke外部的配电网具有低关联度,因而Stroke的内部简化对配电网的影响局限于Stroke的内部,而不会扩展到Stroke的外部配电网,有利于简化。
定义配电网Stroke:
| $ \left\{\begin{array}{l} X=\left\{X_{1}, X_{2}, \cdots, X_{a}\right\} \\ S t=\left\{S t_{1}, S t_{2}, \cdots, S t_{\beta}\right\} \end{array}\right. $ | (1) |
式中,X表示配电网中的线段集合,包括导线段和电缆段;Xα表示其中的第α条线段;St表示Stroke集合,Stβ表示第β条Stroke。
则配电网Stroke划分等价于将集合X分成β个集合St1, St2, ..., Stβ, 并且满足以下3个条件:
| $ \left\{\begin{array}{l} S t_{i} \neq \varnothing, i=1, 2, \cdots, \beta \\ \bigcup_{i=1}^{\beta} S t_{i}=S t \\ S t_{i} \cap S t_{j}=\varnothing, i \neq j, i, j=1, 2, \cdots, \beta \end{array}\right. $ | (2) |
式中,St表示Stroke集合;Sti表示第i个Stroke;β为划分Stroke的个数。
根据以上Stroke定义,对配电网Stroke划分流程如下:
1) 根据配电网中线路的名称,构建初始化Stroke集合,将每一条线路作为一个初始Stroke,同时构建目标Stroke集合作为输出集合;
2) 对每一条Stroke进行遍历,为了保证简化后的配电网的输电特性不变,如果Stroke中存在T节点,在T节点处将Stroke打断并划分为多个子Stroke;若Stroke中不存在T节点,则将该Stroke输出到目标Stroke集合,同时在原始Stroke集合中将该Stroke移除;
3) 对于步骤2)中的子Stroke集合归并到步骤1)初始化Stroke集合,循环执行步骤1)和步骤2),直至初始化Stroke集合为空。
4) 最终得到目标Stroke集合St={St1, St2, …, Stβ}。
经划分后的配电网Stroke由导线段或者电缆段在杆塔处连接而成。每个配电网Stroke相对独立存在,Stroke中不存在T节点,Stroke内部的简化不会对Stroke外部配电网产生影响。
1.2 基于特征点的道格拉斯-普克算法在充分考虑配电网特征和节点差异性的基础上,本文将配电网线路节点分为可被简化和不可被简化两类,在道格拉斯-普克算法的基础上,提出基于特征点的道格拉斯-普克算法,核心思想为:针对只包含可被简化节点配电网Stroke,沿用传统的道格拉斯-普克算法,针对包含不可被简化节点的配电网Stroke,采用特殊的处理方法。
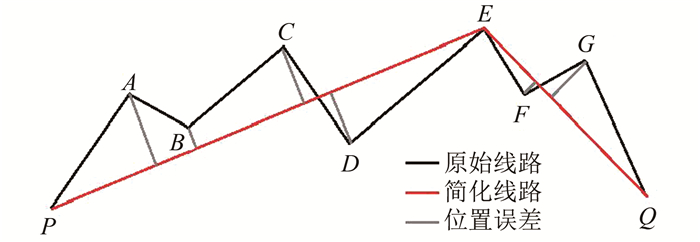
对于配电网Stroke中的不可被简化节点,本文引入位移限差η,基于节点到Stroke基线的距离与位移限差η的差值决定节点是否以投影的方式保留。若差值小于0,则将该节点以垂直投影的方式投影到Stroke基线上;反之,说明该节点投影到Stroke基线上会产生过大的位移误差,且该位移误差不可被接受,则以该节点为中间节点,将Stroke切分为两段子Stroke,而该节点以原始坐标位置予以保留,两段子Stroke递归循环以上处理步骤。如图 1所示,Stroke PQ中,连接PQ,中间各节点A、B、C、D、E、F、G到直线PQ的距离都小于简化阈值λ,按照道格拉斯-普克算法,中间各节点都应被简化删除,但是点C、E、G为不可被简化节点,且点E距离线段PQ的距离Dz>η,则E点被直接保留,并以E为分割点,将Stroke PQ划分为两个子Stroke PE和EQ。图 2中,点C到线段PE以及点G到线段EQ的距离均小于η,则将点C和点G以垂直投影的方式分别投影到线段PE和EQ上,同时删除节点A、B、D、F,简化后的Stroke如图 3所示。
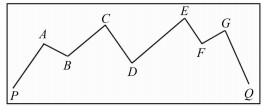 |
| 图 1 原始Stroke Fig.1 Original Stroke |
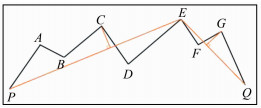 |
| 图 2 Stroke简化示意图 Fig.2 Stroke Simplified Diagram |
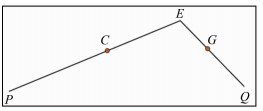 |
| 图 3 简化后的Stroke Fig.3 Simplified Strok |
算法具体步骤如下:
1) 根据导线段和电缆段的所属线路以及线路中的T节点将配电网划分为Stroke集合St;
2) 从St集合中任选一初始Stroke,计算Stroke中的点Pi(i=2, 3, …, N-1)到Stroke首末点所成线段的最大距离D;
3)比较D与简化阈值λ的大小,若D>λ, 则将Stroke切分为两个子Stroke,重复步骤2),反之,执行步骤4);
4) 判断Stroke中是否存在不可简化节点,若不存在不可简化节点,则删除Stroke上除首末端点以外的所有节点,此Stoke简化完毕,若存在不可简化节点,执行步骤5);
5) 计算所有不可简化节点到Stroke首末端点所成线段的最大距离Dz,比较Dz与位移限差η的大小,若Dz>η, 则将Stroke再次切分为两个子Stroke,执行步骤4),反之,执行步骤6);
6) 将Stroke上的不可简化节点以垂直投影的方式映射到由Stroke首末端点连成的线段上,并删除Stroke上除首末端点外的其他可简化节点,此Stroke的简化完毕;
7) 返回执行步骤2),直至St集合为空,整个配电网站外图形简化完毕。
1.3 DP阈值优化基于Stroke的道格拉斯-普克算法简化后的配电网站外线路节点数N随着简化阈值λ的增大不断减小,并且最终趋于一个稳定值,其中,简化阈值λ代表简化力度的大小,而曲线简化后剩余的节点数N则可以衡量曲线的简化效果以及简化后曲线的几何特征保留程度。即不同的简化阈值λ产生不同的简化效果,体现在简化前后曲线上特征点数量的差异上。因此,阈值优化问题可以归结为在λ-N函数关系中取的一个最佳平衡点,同时兼顾简化力度和简化效果。
本文分析简化算法的阈值和曲线简化后剩余的节点数的关系,利用最小二乘曲线拟合[11-13]的方法取得简化阈值与曲线简化后剩余节点数的函数关系,N=f(λ)。取曲线f(λ)曲率最大K所对应的阈值λ,此处作为曲线弯曲程度最大的点,该点处的阈值即代表压缩率与图形几何质量间的最大平衡点,当λk>λ后,随着λk的增大,数据的压缩量会越来越小,并且因为某些关键节点被删除而严重影响图形的几何质量。具体步骤如下:
1) 确定有意义的DP简化阈值取值范围(λmin, λmax)以及步长Δ,其中λmin、λmax、Δ取值可根据数据地理范围基于经验值设定;
2) 以不同取值的λ迭代基于特征点的道格拉斯-普克算法,并统计配电线路节点总数N;
3) 基于最小二乘法拟合λ-N,确定函数关系式N=f(λ);
4) 计算f(λ)导数,使导数值最大的λk即为最佳DP阈值。
2 实验与结果分析 2.1 DP阈值优化实验本文实验数据为湖北省鄂州市高压配电网数据,根据经验值确定的简化阈值的取值范围为[0, 0.04],起始阈值为0,增长步长为0.000 1,迭代基于特征点的道格拉斯-普克算法,记录简化阈值及简化后曲线节点数,共计获得400组数据。
以指数函数为拟合模型,用最小二乘法对阈值-节点数散点图进行曲线拟合,如图 4所示,所得函数关系式见式(3),拟合优度为0.971 3。
| $ f(\lambda)=334.6 \cdot \mathrm{e}^{-475.5 \lambda}+114.2 \cdot \mathrm{e}^{-13.85 \lambda} $ | (3) |
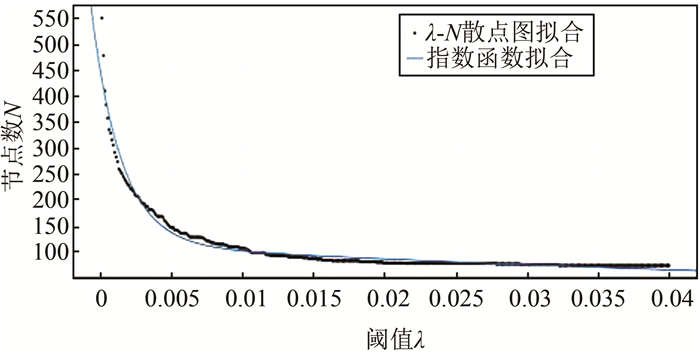 |
| 图 4 最小二乘法拟合结果 Fig.4 The Least Square Fitting Result |
计算拟合函数的曲率:
| $ K=\frac{\left|f^{\prime \prime}\right|}{\left(1+\left(f^{\prime}\right)^{2}\right)^{\frac{3}{2}}} $ | (4) |
并选取使得曲率最大的简化阈值为最优的简化阈值,如图 5所示,得λk=0.011。
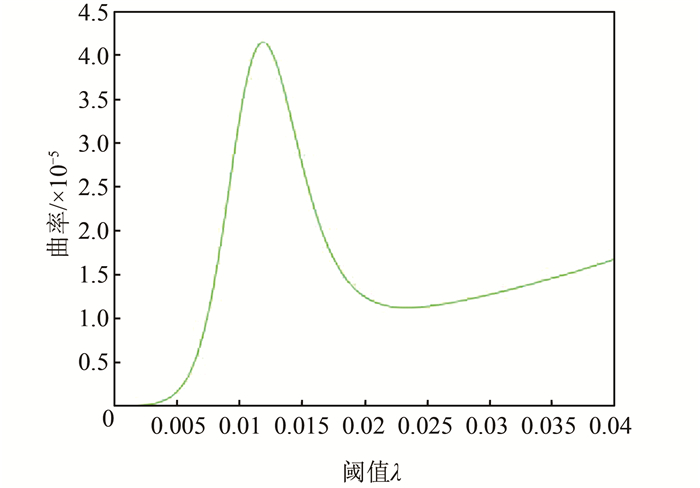 |
| 图 5 拟合函数曲率图 Fig.5 Curvature of the Fitting Function |
2.2 地理接线图简化效果
本文选取最佳简化阈值λ=0.011及其邻近阈值设立对照实验,结果如图 6所示。
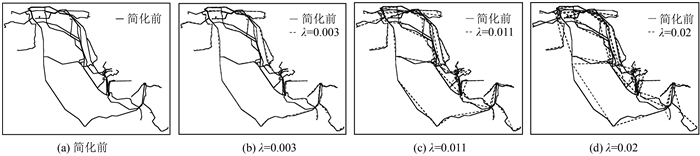 |
| 图 6 不同阈值的地理接线图 Fig.6 Simplified Result with Different Threshold |
如图 6(a)所示,简化前的湖北省鄂州市高压配电网地理接线图存在大量的弯曲特征,在局部区域甚至有多条配电线路重叠在一起,可视化效果极差,难以分辨,严重妨碍配电网规划人员决策。线路简化的本质是移除线路上冗余点,对弯曲特征进行取舍。本文算法基于简化阈值λ移除冗余点,简化阈值越小,移除冗余点越少,弯曲特征保留得越多,随着简化阈值增大,移除冗余点增多,简化后线路保留弯曲特征减少。图 6(b)为λ取0.003时简化地理接线图与原始线路图对比,此时简化阈值较小,简化后的线路仍然保留大量弯曲特征,与原始线路图差别较小,可视化效果提升不足。图 6(d)为λ取0.02简化地理接线图与原始线路图对比,此简化阈值下,舍去大量弯曲特征,能明显区分不同线路,但大量特征点被移除造成线路变形严重。图 6(c)为最佳简化阈值下的简化效果对比图,冗余点去除以及弯曲特征保留较为合理,实现复杂配电网线路的简化,可视化效果得到提升,同时避免因过度简化造成线路严重失真。说明基于最优简化阈值对配电网地理接线图进行简化,能兼顾简化力度和控制变形,提升可视化效果同时避免关键位置节点被移除导致图形严重变形。
图 7为简化前和阈值λ分别取0.003、0.011和0.02时地理接线图局部简化效果。如图 7(a)所示,简化前的地理接线图线路十分密集,难以区分不同的线路。图 7(b)为λ取0.003时的简化效果,仍然存在线路重叠,无法辨析的情况。图 7(d)为λ取0.02的简化效果,此时简化阈值过大,一些决定图形几何质量关键点被删除,线路严重变形。图 7(c)为最佳简化阈值λ取0.011的简化效果图,线路只保留大体轮廓,大量的弯曲被简化,不同的线路清晰可辨。对比分析说明,基于最优阈值对配电网地理接线图进行简化,可有效平衡简化粒度和可视化效果,在两者之间寻求平衡点,防止因简化力度过大而导致图形严重失真,也避免因简化力度过小而无法提升可视化效果。
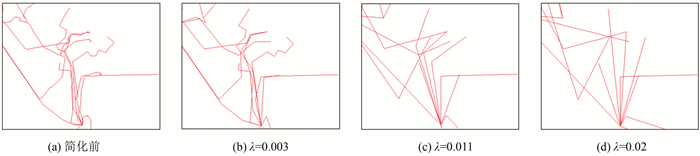 |
| 图 7 不同简化阈值地理接线图局部简化效果图 Fig.7 Local Simplified Result with Different Threshold |
2.3 简化误差分析
配电网地理接线图简化本质上是线要素简化,简化过程中节点数减少,线要素的位置、长度和几何形态发生变化,从而使得地理接线图扭曲失真,简化程度越高,失真越严重。本文通过比较长度误差、基于偏移距离的位移误差和基于偏离面积的位移误差来衡量不同简化阈值引起的几何误差[14-16]。
线路长度是配电网最基本的几何特征,计算简化前后线路的相对长度误差可以定量的衡量简化误差。
| $ \varepsilon=\left(L-L^{\prime}\right) / L $ | (5) |
式中,ε为线路长度误差; L为原始线路长度; L′为简化后的线路长度。
则整个配电网地理接线图的平均长度误差为:
| $ \delta_{L}=\frac{1}{n} \sum\limits_{k=1}^{n} \varepsilon_{k} $ | (6) |
式中,n为配电网中线路总数;δL为平均长度误差。
如图 8所示,基于偏移距离的位移误差可由原始线路节点到简化后线路的垂直距离之和计算得到:
| $ \delta_{H}=\frac{1}{m} \sum\limits_{i=1}^{m} d_{i} $ | (7) |
 |
| 图 8 基于距离的位移误差 Fig.8 Displacement Error Based on Distance |
式中, δH为平均距离误差;di为点pi到简化线路的距离;m为配电网中节点总数。
基于偏离面积的位移误差同时兼顾线路简化的长度误差和位置误差,采用简化线路与原始线路所围成的面积衡量线路简化的几何误差,如图 9所示,其表达式为:
| $ \delta_{S}=\frac{1}{n} \sum\limits_{k=1}^{n} \Delta_{k} $ | (8) |
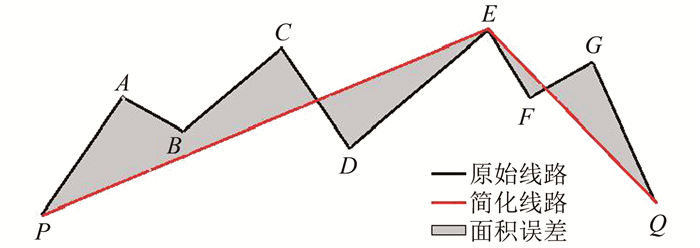 |
| 图 9 基于面积的位移误差 Fig.9 Displacement Error Based on Area |
式中,δS为平均面积误差;Δk为第k条线路的面积误差;n为配电网中线路总数。
不同的简化阈值生成的配电网地理接线图简化程度不同,简化阈值λ越大,简化程度越大,引起的几何误差越大,采用不同简化阈值下配电网地理接线图的几何误差和数据压缩率如表 1所示。可以看出,简化阈值取0.003时,简化后的地理接线图几何误差较小,平均面积误差为0.55,但数据压缩率较低,仅为22%,此时的配电网简化效果并不明显,网架分布依然密集交错, 见图 7(b);当简化阈值取0.02时,平均距离误差和平均面积误差迅速增大,数据压缩率分别为57,但是平均面积误差已经达到5.97,此时的配电网已经产生较为严重的变形和失真,见图 7(d);当简化阈值取0.011时,数据压缩率为45.8%,平均长度误差为9.7%,平均距离误差为279.6 m,平均面积误差为3.3 km2,数据压缩和几何误差较为平衡,兼顾平衡简化力度和数据可视化效果,见图 7(c)。随着简化力度越大,图形越简洁清晰,但是同时变形和失真同样越严重,几何误差越大。因而兼顾网架可视化清晰度的同时保证几何误差尽可能的小十分重要,最佳阈值能够平衡二者的关系,实现最优化配电网图形简化。
| 表 1 不同简化阈值地理接线图几何误差及压缩率 Tab.1 Geometric Errors And Compressibility of Simplified Result with Different Threshold |
 |
3 结束语
针对当前配电网网架模型过于复杂,存在大量冗余设备及信息,基于网架模型生成的地理接线图不适合用于配电网规划的问题,提出一种面向配电网规划的地理接线图简化方法,该方法通过Stroke划分策略将原始复杂的配电网结构转化为高内聚低耦合的Stroke结构,利用特征点的道格拉斯-普克算法对Stroke结构的配电网进行图形简化,基于最小二乘法计算最佳简化阈值实现最优的简化力度与可视化效果的平衡。本文提出的简化方法同时兼顾配电设施的空间位置和线路的拓扑关系,实现配电网可视化图形的优化。该方法可作为从原始配电网数据到规划配电网规划数据的转换算法,为配电网规划提供基础数据支撑。
| [1] |
孔涛, 程浩忠, 李钢, 等. 配电网规划研究综述[J]. 电网技术, 2009, 33(19): 92-99. |
| [2] |
Rao P S N, Deekshit R. Visibility representation of distribution system one-line diagrams[C]. TENCON 2003, Conference on Convergent Technologies for Asia-Pacific Region, Bangalore, India, 2003
|
| [3] |
宋峰, 吴雷平, 廉伟, 等. 一种基于航拍图像识别的电网地理接线图绘制方法: 中国, CN105426825A[P]. 2016-03-23
|
| [4] |
章坚民, 陈昊, 周明磊, 等. 配电网均匀接线图生成及态势图察觉度计算[J]. 电力系统自动化, 2014, 38(13): 166-173. DOI:10.7500/AEPS20130909003 |
| [5] |
刘行波, 李源林, 万林, 等. 一种面向电网规划的地理接线图线路自动定向与接边方法: 中国, CN105512817A[P]. 2016-04-20
|
| [6] |
刘志松, 孙皓, 马亮, 等. 一种面向电网规划的地理接线图自动抽稀方法: 中国, CN105550256A[P]. 2016-05-04
|
| [7] |
靳海亮, 康建荣, 高井祥. 利用等高线数据提取山脊(谷)线算法研究[J]. 武汉大学学报·信息科学版, 2005, 30(9): 809-812. |
| [8] |
Li C M, Wu P D, Gu T, et al. A Study on Curve Simplification Method Combining Douglas-Peucker with Li-Openshaw[M]. Singapore: Springer, 2017: 286-294.
|
| [9] |
Li L L, Jiang W S. An Improved Douglas-Peucker Algorithm for Fast Curve Approximation[C]. Image and Signal Processing (CISP), 2010 3rd International Congress, Yantai, China, 2010
|
| [10] |
Xie Z, Wang H M, Wu L. The Improved Douglas-Peucker Algorithm Based on the Contour Character[C]. 19th International Conference on Geoinformatics, Shanghai, China, 2011
|
| [11] |
孙同贺, 闫国庆, 燕志明. 基于稳健初值的混合总体最小二乘直线拟合[J]. 测绘地理信息, 2016, 41(1): 11-13. |
| [12] |
姚宜斌, 黄书华, 孔建, 等. 空间直线拟合的整体最小二乘算法[J]. 武汉大学学报·信息科学版, 2014, 39(5): 571-574. |
| [13] |
孔建, 姚宜斌, 吴寒. 整体最小二乘的迭代解法[J]. 武汉大学学报·信息科学版, 2010, 35(6): 711-714. |
| [14] |
肖峻, 崔艳妍, 王建民, 等. 配电网规划的综合评价指标体系与方法[J]. 电力系统自动化, 2008(15): 36-40. |
| [15] |
武芳, 朱鲲鹏. 线要素化简算法几何精度评估[J]. 武汉大学学报·信息科学版, 2008, 33(6): 600-603. |
| [16] |
朱鲲鹏. 线要素化简算法质量评估[D]. 郑州: 信息工程大学, 2007
|
 2021, Vol. 46
2021, Vol. 46


