| 全站仪建筑物立面图测量方法研究及工程实践 |
2. 闽江学院,福建 福州,350108;
3. 武汉大学灾害监测和防治研究中心, 湖北 武汉, 430079
2. Minjiang University, Fuzhou 350108, China;
3. Hazard Monitoring & Prevention Research Center, Wuhan University, Wuhan 430079, China
立面图是城市建筑物外观装修和景观改造设计和施工中的重要依据。传统的利用皮尺手工测量或手持测距仪的立面测量方法工作效率较低,累积误差大,而利用全站仪进行立面测量具有快速、高效、无接触等优点,为测制建筑物的立面图提供了一种全新的技术手段。本文介绍了利用全站仪立面测量的方法和原理及其精度分析,结合湄洲岛立面改造项目对实践中的问题提出了解决方法。
1 全站仪立面测量原理及精度分析 1.1 全站仪立面测量原理将建筑物不同的立面投影到与立面平行的铅垂面上,然后按一定比例尺缩小而得到的正射投影图,称为建筑立面图,简称立面图[1]。假设某待测建筑的外墙面如图 1所示,面ABCD为待测的正立面,点A、B、P均在该立面上,S、T为待测立面附近的控制点。A、B两点为外业观测中选定的处于同一水平线上的两点,设A为立面坐标系的原点,
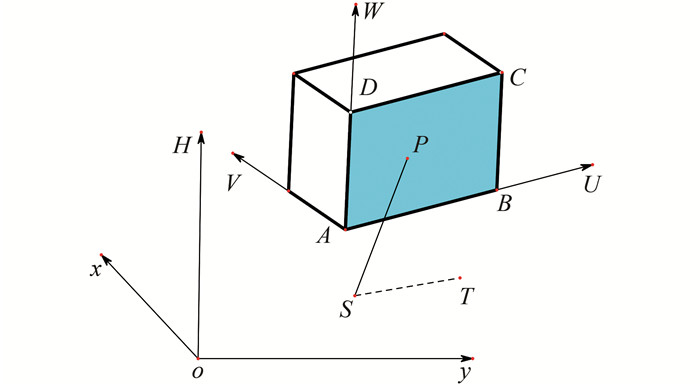 |
| 图 1 立面坐标转换示意图 Figure 1 Sketch Map of Elevation Coordinate Transformation |
立面测量时,全站仪架设在S测站点上,T为后视点,照准目标P点,根据全站仪测量原理得[2]:
| $ \left\{ \begin{array}{l} {x_P} = {x_S} + {S_{SP}} \cdot \sin {Z_{SP}} \cdot \cos ({\alpha _{ST}} + \beta )\\ {y_P} = {y_S} + {S_{SP}} \cdot \sin {Z_{SP}} \cdot \sin ({\alpha _{ST}} + \beta )\\ {H_P} = {H_S} + {S_{SP}} \cdot \cos {Z_{SP}} + i-v \end{array} \right. $ | (1) |
式中, (xS, yS, HS)、(xP, yP, HP) 分别为S、P点在测量坐标系中的三维坐标;αST是
依此原理可求出建筑物上A、B、P等点在测量坐标系中的坐标。
立面图的投影面是铅垂面,而不是地形测量中的水平面[3-7],所以在使用成图软件绘制立面图时,需要对立面测量的数据进行坐标转换。即需要求出所需立面上各特征点在立面坐标系U-V-W中的三维坐标,从而得到各特征点在所需立面上的准确投影位置,据此绘制出相应的立面图。以 (xA,yA,HA)、(xB,yB,HB)、(xP,yP,HP) 表示A、B、P在测量坐标系中的坐标,则根据各点的几何关系可得式 (2):
| $ \left\{ \begin{array}{l} {U_P} = {S_{AP}} \cdot {\rm{cos}}{\beta _P}\\ {V_P} = {\rm{ }}{S_{AP}} \cdot {\rm{sin}}{\beta _P}\\ {W_P} = {H_P}-{H_A} \end{array} \right. $ | (2) |
式中,
根据上述原理对测得的立面特征点逐个进行转换,可计算出各特征点在立面坐标系中的三维坐标。在将数据导入成图软件时,将U-A-W平面作为投影面进行展点绘制,即可得到所需的立面图。
1.2 全站仪立面测量精度分析采用上述方法,每次测量均为独立测量,根据全站仪的测量原理,进行误差分析。考虑A、B为已知点,最后得到点位坐标公式:
| $ \begin{array}{*{20}{l}} {U = {U_A} + S \cdot {\rm{cos}}\alpha \cdot {\rm{sin}}\theta }\\ {W = S \cdot {\rm{sin}}\alpha-{H_A}} \end{array} $ |
式中,α为单次观测的垂直角;θ为观测方位角;S为测站点至照准点的距离。
将上述公式线性化,按误差传播定律,考虑全站仪水平角与垂直角半测回角度测量中误差相同,设为mα,测距中误差设为md,可得到立面坐标中误差关系式:
| $ \begin{array}{l} {m_U}^2 = {\rm{ co}}{{\rm{s}}^2}\alpha \cdot {\rm{si}}{{\rm{n}}^2}\theta \cdot {m_d}^2 + {S^2} \cdot \left( {{\rm{co}}{{\rm{s}}^2}\alpha \cdot {\rm{co}}{{\rm{s}}^2}\theta + {\rm{si}}{{\rm{n}}^2}\alpha \cdot {\rm{si}}{{\rm{n}}^2}\theta } \right) \cdot {m_\alpha }^2\\ {m_W}^2 = {\rm{si}}{{\rm{n}}^2}\alpha \cdot{m_d}^2 + {S^2}\cdot{\rm{co}}{{\rm{s}}^2}\alpha \cdot{m_\alpha }^2 \end{array} $ |
则待测点的点位中误差为:
| $ \begin{array}{l} {m_P}^2 = {\rm{ }}({\rm{co}}{{\rm{s}}^2}\alpha \cdot {\rm{si}}{{\rm{n}}^2}\theta + {\rm{si}}{{\rm{n}}^2}\alpha ) \cdot {m_d}^2 + {S^2} \cdot \\ \left( {{\rm{co}}{{\rm{s}}^2}\alpha \cdot {\rm{co}}{{\rm{s}}^2}\theta + {\rm{si}}{{\rm{n}}^2}\alpha \cdot {\rm{si}}{{\rm{n}}^2}\theta + {\rm{ co}}{{\rm{s}}^2}\alpha } \right) \cdot {m_\alpha }^2 \end{array} $ | (3) |
由式 (3) 可以发现,影响立面测量精度的因素主要体现为测量距离、方向观测值和垂直角的大小。
结合式 (3) 与图 2可以看出,观测方位角为0°~90°时的点位中误差与方位角为270°~360°时的点位中误差相同,故在此只考察0°~90°的情况 (实际测量时方位角无法达到90°,此处仅作为极限条件)。同样,垂直角为-45°~0°时的点位中误差与垂直角为0°~45°时的点位中误差相同,故在此只考察0°~45°的情况。设仪器测距精度md=5+3S mm,仪器一测回方向观测值中误差为2″,则半测回方向观测值中误差为2.8″。以测量斜距100 m,垂直角不超过45°计算,方位角、垂直角和点位中误差变化关系见表 1。
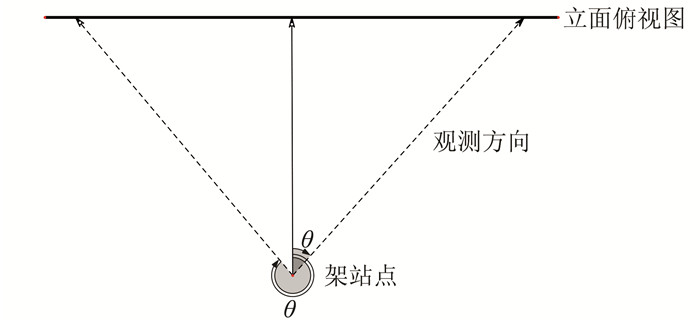 |
| 图 2 测量设置示意图 Figure 2 Sketch Map of Measurement |
| 表 1 不同方位角、不同垂直角的点位中误差表 Table 1 Deviation of Different Azimuth and Vertical Angle |
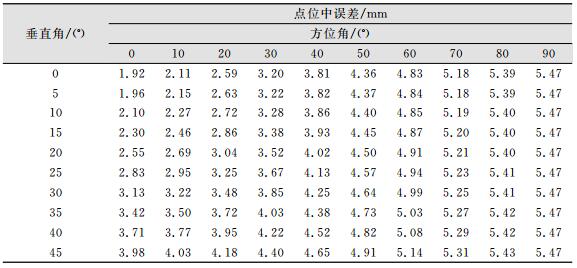 |
由表 1可以发现,在同一方向上,垂直角越大,点位误差越大。而当垂直角一定时,立面各特征点的误差主要是由方位角引起的,随着方位角越接近于90°,误差越大。将方位角与垂直角均取最大值时,测量的最大点位中误差仅取决于测量距离。由式 (3) 计算,方位角与垂直角均取最大值时,测量距离与点位中误差的关系如图 3所示。
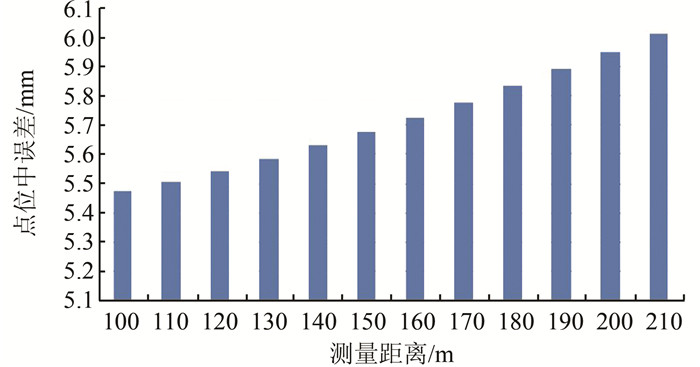 |
| 图 3 不同测量距离的点位中误差 Figure 3 Deviation of Different Measuring Distance |
由图 3可知,当测量距离为200 m,点位中误差为5.95 mm,小于规定的6 mm,故作业时,测量距离不应超过200 m,如在此范围内无法完整测量整个立面,应采用架设支站的方法测量。为了减小误差,支站应尽量选在垂直角和方位角均为0°的地方。
2 工程实践及结果分析福建莆田市政府为提升城市形象,美化城市环境,提高居住品质,提出对湄洲岛主要街道两侧旧建筑的外立面进行综合整治。本文涉及的湄洲岛立面测量工程包括总长约3 km的街道两侧的155栋建筑。立面图的比例尺为1:200,精度要求点位中误差不得大于6 mm,临近立面特征点间距中误差不得大于10 cm。超过2倍中误差为粗差,需重新测量。内业检验要求立面图能反映建筑物外立面面积和各要素的相对位置关系,外立面各特征要素表示正确,无缺漏;图面清晰、美观,图廓整饰正确完整;图示、线性、字体符合要求,以作为设计改造的参照依据。
2.1 外业数据采集外业数据采集前,应做好测站和立面基准点选择工作。测站选择原则为:①通视条件较好;②离待测立面距离适中。测站选择后,用手机拍摄立面图片 (尽量将整个立面拍在一张照片中) 并绘制草图,见图 4。同时,选择两个立面基准点,其原则是:①两点应在同一水平高度;②两点距离尽量远[8];③A点在左,B点在右。如立面基准点可以选择为房屋檐廊的下缘线两端点、雨篷的两端点等等,以便后面的坐标转换。
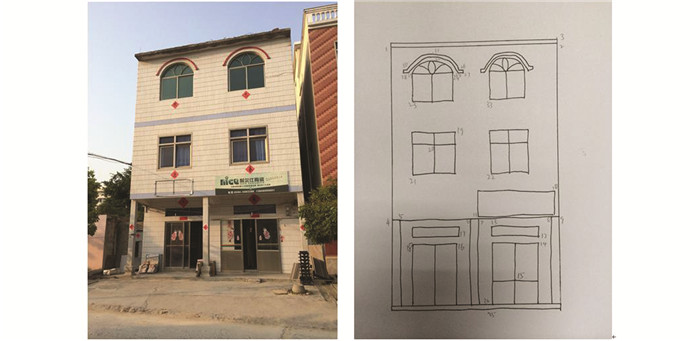 |
| 图 4 待测建筑立面及立面草图 Figure 4 Elevation of the Building to be Measured and Its Sketch |
采用仪器自由架设法,通过测出建筑立面上的房屋主线、屋檐、屋顶、窗户、窗框、门、阳台、防盗网、空调架、台阶等要素,获取立面点的三维坐标,并在草图上的对应位置上标记点号。
当测区较长或建筑物立面通视条件较差 (如行道树较为茂密) 时,如图 5所示,会出现一次架站无法完全观测整个立面的情况,需要通过架设支站的方法解决。两次架站间要选取2~3个易于照准、特征明显的公共点,用来将两站测得的数据进行拼接和检核。每次架站时应注意拍摄照片,以便成图时进行参考。
 |
| 图 5 视线被树木遮挡的情况 Figure 5 Situation of View Blocked by Trees |
2.2 内业数据处理
全站仪的数据导出后,利用Excel的宏功能进行坐标转换。在Excel中建立坐标转换的模板文件,按照立面测量的原理编写宏程序。然后将全站仪导出的数据复制到Excel坐标转换文件中进行转换,图 6为立面测量数据及坐标转换后的数据示意图。图 6中,前5列为标准CASS格式内容。第F列中的a、b为外业观测中选定的立面基准点,a点在水平线的左边,b点在水平线的右边。将转换后的坐标 (G-K列) 复制并另存为csv,改后缀dat即可在CASS中使用。
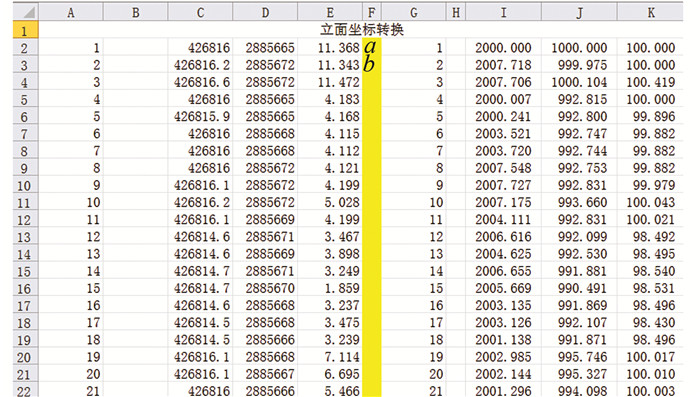 |
| 图 6 立面测量坐标转换文件 Figure 6 Elevation Coordinate Conversion File |
为了清晰地表示立面情况,绘图前需要根据此次项目的要求在CASS软件中定义图层,见图 7。
 |
| 图 7 立面图的分层 Figure 7 Layers of Elevation |
绘制立面图时,先根据转换后的数据文件按要求的比例尺在CASS软件中展点,然后对照立面情况进行连线,最后将立面图的相应部位按图例符号进行图案填充并添加注记等,完成立面图的绘制,得到成图见图 8。如某个立面架设了支站,绘图时应将支站和主站数据在同一个文件中展点,并以两站的公共点为基点将数据拼接,在拼接好的数据上进行
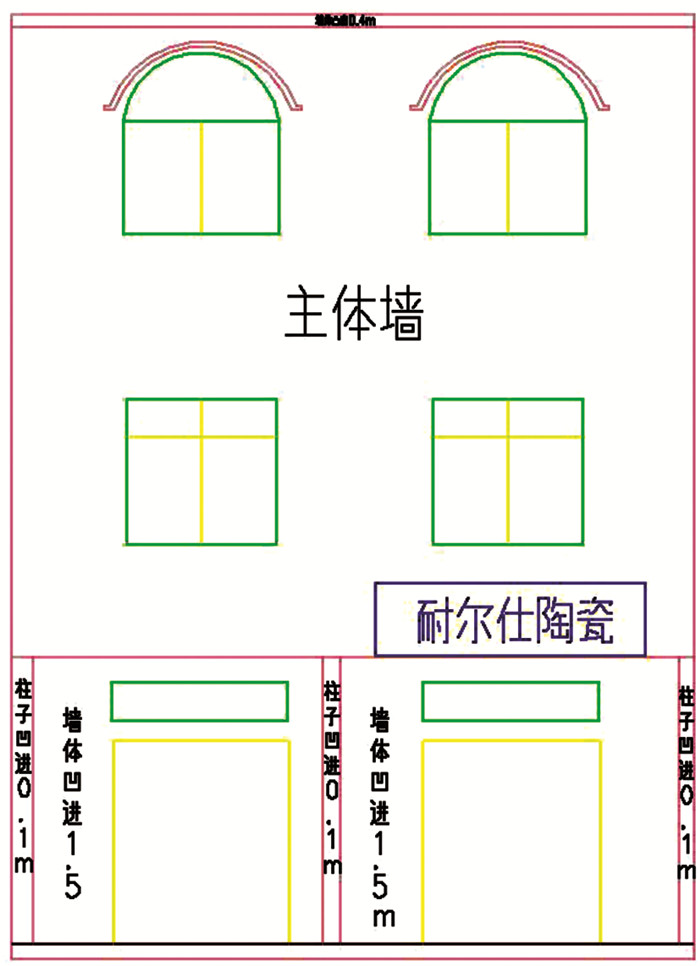 |
| 图 8 立面测量成图 Figure 8 Graph of Elevation Measurement |
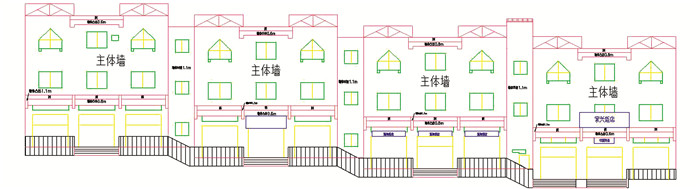 |
| 图 9 进行拼接后的完成图 Figure 9 TFinal Graph After Matching |
2.3 结果分析
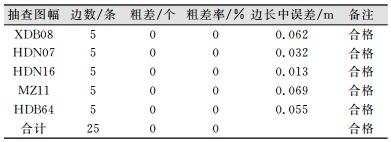
所有立面成果完成后,需要到实地检查,保证各立面要素均无缺失。到实地量取立面上相邻特征点的间距,量测边数每个立面不少于5处,按式 (4) 求取相邻特征点间距中误差。
| $ {M_s} = \sqrt {\frac{{\sum\limits_{i = 1}^n {\Delta S_i^2} }}{{n-1}}} $ | (4) |
式中,ΔSi为相邻特征点实测边长与同名边长的较差;n为量测边条数。检验结果如表 2所示。经检查验收,结果精度符合要求。
| 表 2 相邻特征点间距中误差检查表 Table 2 Deviation of Distance Between Adjacent Feature Points |
 |
3 结束语
传统的皮尺手工测量和手持测距仪等立面测量方法,测量精度差,作业过程繁琐,利用全站仪进行立面测量具有成本低、操作简单、效率高等优点,本文结合了湄洲岛立面测量工程对这种方法流程进行了介绍。由文中所述,此种方法的测量精度与仪器架设位置和观测角度有较大关系,在实际施工时应仔细选择仪器架设位置,以保证测量精度。
| [1] | 杨志华. 房屋建筑学[M]. 北京: 中国建筑工业出版社, 2010. |
| [2] | 潘正风, 程效军, 成枢, 等. 数字测图原理与方法[M]. 2版. 武汉: 武汉大学出版社, 2009. |
| [3] | 廖小辉, 李燕, 胡云世, 等. 古建筑保护测绘方法的研究[J]. 测绘通报, 2008, (12): 45–46. |
| [4] | 李军杰. 测绘工程CAD[M]. 郑州: 黄河水利出版社, 2008. |
| [5] | 别建晓. 建筑物立面测量的研究[J]. 城市勘测, 2011, (3): 141–143. |
| [6] | 向继平, 刘省姣. 建筑物立面测量方法的研究与实践[J]. 测绘与空间地理信息, 2013, 36(10): 220–222. |
| [7] | 江金霞, 吴卓珈, 陈德标. 廊桥立面测量方法研究[J]. 北京测绘, 2010, (4): 43–45. |
| [8] | 张景湘, 马捷, 赵龙平. 起始方位角误差对附合导线平差结果的影响[J]. 测绘科学技术学报, 2006, 23(1): 62–64, 68. |
 2017, Vol. 42
2017, Vol. 42

