| 罗德里格矩阵对自检校误差模型精度影响的研究 |
对于三维激光扫描系统而言,测角及测距误差是其主要的系统误差之一[1, 2]。本文利用三维激光扫描仪及全站仪对变形点进行对比监测实验,提出一种基于罗德里格矩阵的扫描仪系统误差自检校模型,并讨论扫描仪测角、测距系统误差改正前后对实验结果的影响,并对此改正模型的适用性作出评价[3]。
1 自检校误差模型 1.1 常规自检校误差模型地面三维激光扫描仪可视为一台无合作目标测距、可以高速动态测角的全站仪,参照全站仪的误差来源,基于布尔莎空间坐标系转换模型(不考虑尺度因子),构建了包含6个外部定向参数(旋转、平移参数)及5个仪器系统误差参数的自检校误差模型。
| $ f = \left[ \begin{array}{l} X\\ Y\\ Z \end{array} \right] = R\left( {\mathit{\Phi , \Omega , {\rm K}}} \right)\left[ \begin{array}{l} x\\ y\\ z \end{array} \right] + \left[ \begin{array}{l} \Delta X\\ \Delta Y\\ \Delta {\rm Z} \end{array} \right] $ | (1) |
但该模型在构造误差方程式时,旋转参数R线性化要顾及3个角度的象限问题,计算过程繁琐,且计算量大。针对该缺点,本文提出基于罗德里格矩阵的自检校误差改正模型,并对此改正模型的适用性作出评价[4]。
1.2 罗德里格矩阵简介旋转矩阵R是一个具有3个自由度的正交矩阵,即自身的9个元素是由3个独立角度数值构成的。设S矩阵为反对称矩阵,由3个独立未知数a、b、c构成,如式(2)所示:
| $ \mathit{\boldsymbol{S = }}\left[ {\begin{array}{*{20}{c}} 0&{ - c}&{ - b}\\ c&0&{ - a}\\ b&a&0 \end{array}} \right] $ | (2) |
则R可用S组成的罗德里格矩阵表示,具体构成式可表示为:
| $ \mathit{\boldsymbol{R}} = \left( {\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{S}}} \right){\left( {\mathit{\boldsymbol{E}} - \mathit{\boldsymbol{S}}} \right)^{ - 1}} $ | (3) |
式中,E为3阶单位矩阵。基于以上理论,可知原本由3个独立的旋转角参数来求解旋转矩阵R可以转换为由3个独立的实参数来求解[5],因此计算更为简单。
1.3 基于罗德里格矩阵的自检校误差模型由式(2)得,矩阵R由矩阵S的3个相互独立的参数[6, 7]具体表示如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{R}}\left( {a, b, c} \right) = \\ \frac{{\left[ {\begin{array}{*{20}{c}} {1 + {a^2} - {b^2} - {c^2}}&{ - 2ab - 2c}&{ - 2b + 2ac}\\ {2c - 2ab}&{1 - {a^2} + {b^2} - {c^2}}&{ - 2a - 2bc}\\ {2ac + 2b}&{2a - 2bc}&{1 - {a^2} - {b^2} + {c^2}} \end{array}} \right]}}{{1 + {a^2} + {b^2} + {c^2}}} \end{array} $ | (4) |
则基于罗德里格矩阵的坐标转换公式为:
| $ f = \left[ \begin{array}{l} X\\ Y\\ Z \end{array} \right] = {\rm{ }}\mathit{\boldsymbol{R}}\left( {a, b, c} \right)\left[ \begin{array}{l} x\\ y\\ z \end{array} \right] + \left[ \begin{array}{l} \Delta X\\ \Delta Y\\ \Delta Z \end{array} \right] $ | (5) |
式中,(x, y, z)为扫描坐标系下的数据集p;(X, Y, Z)为外部坐标系下的的数据集q。参照扫描仪与全站仪有相似的测距、测角误差源[8],则扫描坐标系下的点位坐标(x, y, z)可表示为:
| $ \left[ \begin{array}{l} x\\ y\\ z \end{array} \right] = \left[ \begin{array}{l} (D + m + \lambda D){\rm{cos}}(\theta + \zeta ){\rm{cos}}\left[ {\alpha + h + i} \right]\\ (D + m + \lambda D){\rm{cos}}(\theta + \zeta ){\rm{sin}}\left[ {\alpha + h + i} \right]\\ (D + m + \lambda D){\rm{sin}}\left( {\theta + \zeta } \right) \end{array} \right] $ | (6) |
式中,m、λ分别为测距加常数、测距乘常数;ζ为竖盘指标差;h为瞄准轴误差; i为水平轴误差,这5个参数便是仪器的测角、测距系统误差参数[9, 10]。
综上所述,基于罗德里格矩阵的坐标转换公式,本文提出的自检校误差改正模型包括3个独立实参数(a, b, c)、3个平移参数(ΔX, ΔY, ΔZ)及5个扫描仪测角测距系统误差参数(m, λ, ζ, h, i)[11]。视外部坐标系统下的观测值(X, Y, Z)为参考基准,认为扫描坐标系下的观测值中含有误差,对于第j对同名点对,可列误差方程式[12, 13]:
| $ \begin{array}{l} \;\;\;\;{v_j} = {\left( {\frac{{\partial f}}{{\partial a}}} \right)_j}{\rm{d}}a + {\left( {\frac{{\partial f}}{{\partial b}}} \right)_j}{\rm{d}}b + {\left( {\frac{{\partial f}}{{\partial b}}} \right)_j}{\rm{d}}c + \\ {\left( {\frac{{\partial f}}{{\partial \Delta X}}} \right)_j}{\rm{d}}\Delta X + {\left( {\frac{{\partial f}}{{\partial \Delta Y}}} \right)_j}{\rm{d}}\Delta Y + {\left( {\frac{{\partial f}}{{\partial \Delta Z}}} \right)_j}{\rm{d}}\Delta Z + \\ \;\;\;\;\;\;\;\;{\left( {\frac{{\partial f}}{{\partial m}}} \right)_j}{\rm{d}}m + {\left( {\frac{{\partial f}}{{\partial \lambda }}} \right)_j}{\rm{d}}\lambda + {\left( {\frac{{\partial f}}{{\partial \zeta }}} \right)_j}{\rm{d}}\zeta + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {\frac{{\partial f}}{{\partial h}}} \right)_j}{\rm{d}}h + {\left( {\frac{{\partial f}}{{\partial i}}} \right)_j}{\rm{d}}i - {\mathit{\boldsymbol{l}}_j} \end{array} $ | (7) |
其中,
| $ {\mathit{\boldsymbol{v}}_j} = \left[ \begin{array}{l} {v_x}_j\\ {v_y}_j\\ {v_z}_j \end{array} \right], {\mathit{\boldsymbol{l}}_j} = {f_j} - {f_j}^0 = \left[ \begin{array}{l} {l_x}_j\\ {l_y}_j\\ {l_z}_j \end{array} \right]。$ |
当共有s对同名点对时,可得到总的误差方程如式(8)所示:
| $ \underset{3s \times 1}{\boldsymbol{V}}=\underset{3s \times 11}{\boldsymbol{B}} \underset{11 \times 1}{\boldsymbol{x}}-\underset{3s\times 1}{\boldsymbol{l}} $ | (8) |
根据间接平差的理论进行解算,可得
| $ {\mathit{x}}{\rm{ = }}{({{\mathit{\pmb{B}}}^{\rm{T}}}{\mathit{\pmb{B}}})^{ - 1}}{{\mathit{\pmb{B}}}^{\rm{T}}}{\mathit{\pmb{l}}} $ | (9) |
进行间接平差的迭代计算,直到改正数xi(i表示迭代到第i次)小于给定阈值时停止计算[14],此时Xi即为自检校误差模型未知参数的最终解。
模型的单位权中误差σ0为:
| $ {\sigma _0}{\rm{ = }}\sqrt {\frac{{{{\mathit{\pmb{V}}}^{\rm{T}}}{\mathit{\pmb{V}}}}}{{3s - 11}}} $ | (10) |
对模型未知参数进行求解后,便可以对原始的距离角度观测值(D, α, θ)进行系统误差改正,并利用式(6)对原始的点云坐标数据集p(x, y, z) 进行修正以获取改正后的点云坐标数据集p′(x′, y′, z′),然后利用式(5)及坐标转换参数(a, b, c, ΔX, ΔY, ΔZ),分别求得数据集p(x, y, z)及p′(x′, y′, z′) 在外部坐标系下的坐标集Q(XP, YP, ZP)和Q′(X′p, Y′p, Z′p)。取第i点对,利用式(11)进行自检校模型有效性评定[15]:
| $ \left\{ \begin{array}{l} {\mathit{\Delta }_i} = {\left\| {{q_i} - \left[ {\mathit{\boldsymbol{R}}\left( {a, b, c} \right){p_i} + T} \right]} \right\|^2}{\rm{ = }}{\left\| {{q_i} - {Q_i}} \right\|^2}\\ \mathit{\Delta }{\prime _i} = {\left\| {{q_i} - \left[ {\mathit{\boldsymbol{R}}\left( {a, b, c} \right)p{\prime _i} + T} \right]} \right\|^2}{\rm{ = }}{\left\| {{q_i} - Q{\prime _i}} \right\|^2} \end{array} \right. $ | (11) |
式中,T为平移参数(ΔΧ, ΔY, ΔΖ);利用此公式对所有的同名点对进行计算,可以对比各点对在系统误差改正前后的坐标转换精度变化情况,同时可以进行总体转化精度的对比,即∑Δ与∑Δ′之间的比较。此外,还可以进行同名点对系统误差改正前后的各方向中误差(σx, σy, σz)及点位中误差σp的对比,计算公式见式(12):
| $ \left\{ \begin{array}{l} {\sigma _x}{\rm{ = }}\sqrt {\frac{{\sum {\delta _{_X}^2} }}{n}} \\ {\sigma _{_y}}{\rm{ = }}\sqrt {\frac{{\sum {\delta _{_{_y}}^2} }}{n}} \\ {\sigma _z}{\rm{ = }}\sqrt {\frac{{\sum {\delta _{_z}^2} }}{n}} \\ {\sigma _p}{\rm{ = }}\sqrt {{\sigma _x}^2 + {\sigma _y}^2 + {\sigma _z}^2} \end{array} \right. $ | (12) |
式中,n为同名点数;(δX, δY, δZ)为转换后的同名点对坐标差。
3 新模型适用性分析 3.1 数据采集实验采用立体桥模型作为变形监测主体,在桥体形变特征点位处6个监测点,如图 1所示,通过改变桥模结构位置来模拟变形情况。
 |
| 图 1 监测点分布示意图 Fig.1 Monitoring Point Distribution Diagram |
为了确保数据的可靠性,采用0.5″级高精度徕卡TS30全站仪和Faro Focus3D×120三维激光扫描仪同步对监测点分别进行两次数据采集,其中扫描仪需两个测站采集单次全部监测点数据。6个监测点通过两种仪器观测得到同名点数据结果如表 1所示。
| 表 1 同名点对坐标 Tab.1 Point-to-Point Coordinate Table with the Same Name |
 |
3.2 数据处理和分析
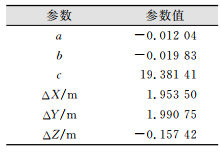
首先,不考虑三维激光扫描仪的系统误差影响,基于罗德里格矩阵的坐标转换公式(5),利用迭代最小二乘法求解三维激光扫描坐标系到全站仪独立坐标系的坐标转换参数,如表 2所示。
| 表 2 未考虑系统误差时的坐标转换参数值 Tab.2 Coordinate Conversion Parameter Values when System Error is Not Considered |
 |
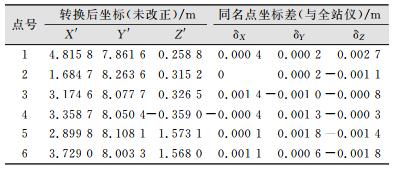
通过表 2的坐标转换参数,利用公式(6)将扫描坐标系下的6个标靶坐标转换到全站仪坐标系下,并求解转换到同一坐标系统下的两套坐标之间的差值,具体如表 3所示。
| 表 3 未考虑系统误差时的坐标转换对比 Tab.3 Coordinate Conversion Comparison Without Considering System Error |
 |
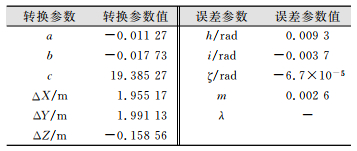
然后认为三维激光的实测数据受测距、测角系统误差的影响,利用自检校误差模型求解坐标转换参数的同时确定相应的误差参数[16-20]。具体结果如表 4所示。
| 表 4 坐标转换参数值与误差参数值 Tab.4 Coordinate Conversion Parameter Value and Error Parameter Value |
 |
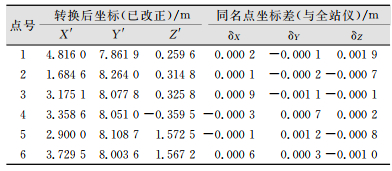
通过表 4的误差参数,首先利用式(6)更新扫描坐标系统下的6个标靶中心坐标值,然后利用转换公式(5)将扫描坐标系统下的6个新标靶中心坐标转换到全站仪坐标系统下,并求解转移到同一坐标系下的两套坐标之间的差值,具体结果如表 5所示。
| 表 5 考虑系统误差时的坐标转换对比 Tab.5 Coordinate Transformation Comparison Considering System Error |
 |
基于式(12),并结合表 3和表 5,分别计算在未考虑系统误差影响和考虑系统误差影响两种情况下的坐标转换精度,结果如表 6所示,其中σx、σy、σz为坐标轴各方向中误差,σp为总体点位中误差。
| 表 6 坐标转换精度结果 Tab.6 Coordinate Transformation Accuracy Result |
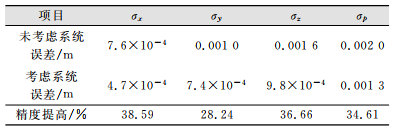 |
对表 6中两种情况下的坐标转换精度进行比较,可以发现,在考虑系统误差影响时,对三维激光扫描数据进行修正,可以有效地降低点位各方向的误差,最少精度提高28.24%,最终的点位中误差也由原来的2 mm减小到转换后的0.13 mm,精度提高了34.61%。
4 结束语本文运用罗德里格矩阵对自检标误差模型进行了推导,提出了有效评定的方法。通过实验数据分析可得,基于罗德里格矩阵的自检校误差模型可以有效地降低三维激光扫描系统误差,较为显著地提高了坐标转换的精度。尤其在三维激光扫描仪多测站采集点云数据时,新自检校误差模型对成果数据的提高表现得更加明显。
| [1] |
袁达. 利用三维激光扫描进行建筑物立面测量的精度分析[J]. 测绘与空间地理信息, 2018, 41(11): 216-218. DOI:10.3969/j.issn.1672-5867.2018.11.064 |
| [2] |
汪仁银, 李开伟, 陈锐, 等. 三维激光扫描技术在地形测绘中的应用[J]. 测绘通报, 2018(12): 159-162. |
| [3] |
官云兰, 程效军, 詹新武, 等. 地面三维激光扫描仪系统误差标定[J]. 测绘学报, 2014, 43(7): 731-737. |
| [4] |
田茂, 花向红, 丁鸽, 等. 基于罗德里格矩阵的混合最小二乘方法在三维激光中的应用[J]. 测绘地理信息, 2014, 39(2): 18-21. |
| [5] |
杨凡, 李广云, 王力, 等. 一种基于罗德里格矩阵的最小二乘迭代坐标转换方法[J]. 工程勘察, 2010(9): 80-84. |
| [6] |
赵启龙. 罗德里格矩阵在三维坐标转换中的应用研究[J]. 北京测绘, 2014(5): 29-30. DOI:10.3969/j.issn.1007-3000.2014.05.008 |
| [7] |
蔡建民, 花向红, 宣伟, 等. 地面三维激光扫描仪系统误差模型研究及精度分析[J]. 测绘地理信息, 2016, 41(5): 17-21. |
| [8] |
陈西江, 花向红, 鲁铁定. 基于组合罗德里格矩阵的异常特征点探测[J]. 测绘科学, 2013, 38(4): 94-96. |
| [9] |
张东, 黄腾, 陈建华, 等. 基于罗德里格矩阵的三维激光扫描点云配准算法[J]. 测绘科学, 2012, 37(1): 156-157. |
| [10] |
陈林宇. 基于罗德里格矩阵的三维坐标转换方法研究[J]. 地理空间信息, 2018, 16(11): 107-109. DOI:10.3969/j.issn.1672-4623.2018.11.031 |
| [11] |
杨福芹, 戴华阳, 邹定辉, 等. 一种公共点坐标系转换中的粗差探测方法及其应用[J]. 测绘通报, 2015(8): 38-41. |
| [12] |
纪超, 丁克良, 张春禄, 等. 基于罗德里格矩阵的整体最小二乘三维坐标转换模型[J]. 北京测绘, 2016(4): 1-5. DOI:10.3969/j.issn.1007-3000.2016.04.001 |
| [13] |
韩梦泽, 李克昭. 基于罗德里格矩阵的空间坐标转换[J]. 测绘工程, 2016, 25(4): 25-27. DOI:10.3969/j.issn.1006-7949.2016.04.006 |
| [14] |
原玉磊, 蒋理兴, 刘灵杰. 罗德里格矩阵在坐标系转换中的应用[J]. 测绘科学, 2010, 35(2): 178-179. |
| [15] |
唐琨, 花向红, 魏成, 等. 基于三维激光扫描的建筑物变形监测方法研究[J]. 测绘地理信息, 2013, 38(2): 54-55. |
| [16] |
程烺, 俞家勇, 马龙称, 等. 单位四元数、罗德里格转换模型与欧拉角的映射关系[J]. 北京测绘, 2020, 34(1): 44-50. |
| [17] |
姚宝玲. 权值对整体最小二乘解算结果的影响分析[J]. 科技创新与生产力, 2018(9): 63-66. DOI:10.3969/j.issn.1674-9146.2018.09.063 |
| [18] |
张卡, 张道俊, 盛业华, 等. 三维坐标转换的两种方法及其比较研究[J]. 数学的实践与认识, 2008, 38(23): 121-128. |
| [19] |
陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报·信息科学版, 2004, 29(12): 1101-1105. |
| [20] |
姚宜斌, 黄承猛, 李程春, 等. 一种适用于大角度的三维坐标转换参数求解算法[J]. 武汉大学学报·信息科学版, 2012, 37(3): 253-256. |
 2021, Vol. 46
2021, Vol. 46

