| 观测时长对不同长度的GNSS基线解算精度影响分析 |
全球定位导航系统广泛应用于大地测量、地壳形变监测、工程测量、导航定位、地球动力学与气候监测、地质灾害监测等领域[1-6]。根据解算方式的不同,GNSS可以分为相对定位和绝对定位两种解算模式[6]。其中,由于相对定位可以很方便地消除卫星和接收机端的钟差、削弱大部分轨道误差以及部分大气误差,在高精度领域应用较为广泛[7, 8]。相对定位的解算精度主要取决于观测时长和基线长度[9, 10]。一般而言,观测时长越长,基线长度越短,基线解算精度就越高。比如,实时动态差分定位(realtime kinematic, RTK)的基线长度一般为几千米至十几千米,只需要数秒即可取得厘米级定位精度[9, 11];而对GNSS变形监测而言,基线长度同样为几千米至十几千米,却需要数小时才可取得毫米级监测精度[10, 12]。
对于大地控制网建立、地壳形变监测等应用领域而言,时效性要求较低,一般采用较长时间的观测来提高解算精度[13]。对于工程测量等应用而言,时效性要求较高,但测量精度要求一般为厘米级,采用RTK或网络RTK技术可以达到即测即得的要求。但是对于部分特殊领域如地质灾害监测,必须同时兼顾时效性和精度[14, 15]。一方面地质灾害发生较为迅速,对解算时效性要求较高;另一方面地质灾害孕育期的变形量较小,对解算精度要求较高。对于不同应用领域,定量分析观测时长对不同长度基线的解算精度的解算时长设置和基线选择有较大的帮助。为探究不同观测时长对不同长度的基线解算精度的影响,选取不同基线长度的若干IGS站,根据不同观测时长利用GAMIT软件进行静态解算,以分析观测时长对不同基线长度的GNSS基线解算精度的影响。
1 数据来源与解算设置根据不同基线距离,基线分为长基线、中基线和短基线3类。其中长基线大于500 km、中基线长度大于20 km并小于100 km、短基线长度小于10 km。长基线选取了ABER、AJAC、BRST、BRUX、BZRG共5个IGS站从2018年3月11日—20日(年积日070~079)的数据。中基线选取了HGHN、HLOB、KOUC、LCAP、PEBO、PMBT、UACO共7个IGS站从2018年3月11日—20日(年积日070~079)的数据。短基线选取了ARHT、DUND、DUNT、FRDN、KIR0、KIR8、KIRU、MCM4、MET3、METG、METS、NMEA、NRMD、NRMG、OUS2、SCTB、STR1、STR2、TID1、TIDB、TIDV、UNBN、UNBJ、WAB2、ZIM2、ZIMJ、ZIMM共27个IGS站从2018年3月11日—20日(年积日070~079)的数据。具体基线长度如图 1所示。
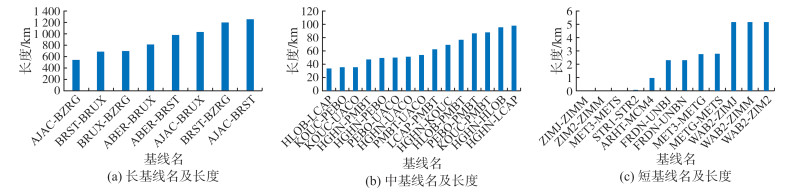 |
| 图 1 长、中、短基线名及长度 Fig.1 Long, Medium, Short Baseline Names and Lengths |
对于长基线,采用24 h时段长度解算,并估计对流层天顶湿延迟和大气梯度采用单天解的模式;对于中基线,采用6 h、8 h、10 h、12 h与24 h的时段长度解算,估计对流层天顶湿延迟;对于短基线,采用1 h、2 h、4 h、6 h、24 h的时段长度解算,不估计对流层天顶湿延迟。
2 结果与分析基线质量评价可分为单时段和多时段,单时段解主要看标准化均方根误差(normalized root-meansquare, NRMS)。一般NRMS优于0.3则认为解算精度较好[2]。对于多时段解算,一般将基线3个分量和边长的基线重复率、固定误差和比例误差作为评价精度的标准[1]。
2.1 长基线图 2为长基线24 h解算的NRMS,由图 2可以看出所有天的NRMS优于0.22,最小值为0.204,满足精密基线解算要求。
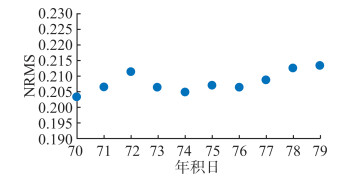 |
| 图 2 长基线NRMS Fig.2 NRMS of Long Baseline |
图 3为长基线24 h解算各方向分量基线重复率。图 3中可以看出,所有基线在N方向和E方向精度优于6 mm,在U方向优于10 mm,在基线长度的基线重复率均优于3 mm。表 1为长基线24 h解算的固定误差和比例误差。由表 1可知,长基线的比例误差可以达到10-9的精度,固定误差可以达到水平方向0.7 mm、竖直方向1.5 mm的精度。同样根据固定误差和比例误差的结果计算,当基线长度为1 000 km时,采用24 h解算,N方向误差3.6 mm, E方向误差3.8 mm, U方向误差6.5 mm。
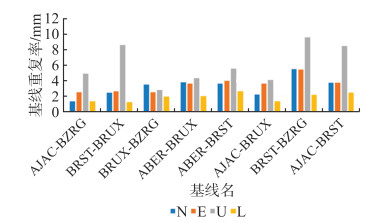 |
| 图 3 长基线各方向上的基线重复率 Fig.3 Baseline Repeat Rate with all Sides of the Long Baseline |
| 表 1 长基线固定误差及比例误差 Tab.1 Fixed Error and Proportional Error of Long Baseline |
 |
2.2 中基线
图 4为中基线解算的NRMS。由图 4可以看出各时段解NRMS优于0.21,符合高精度基线解算要求。
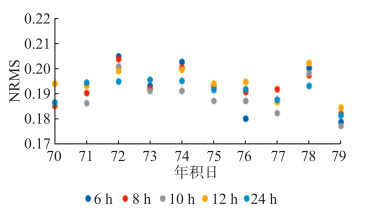 |
| 图 4 中基线NRMS Fig.4 NRMS of Medium Baseline |
图 5为中基线6 h、8 h、10 h、12 h和24 h解算各方向分量基线重复率。由图 5可知,6 h解算N方向和E方向优于8 mm, U方向优于20 mm。8 h解算N方向和E方向优于6 mm, U方向优于18 mm。10 h解算N方向和E方向优于5 mm, U方向除基线HLOB-PMBT外均优于15 mm。大多数基线12 h解算N方向和E方向基线重复率优于4 mm, U方向优于11 mm。24 h解算N方向和E方向的基线重复率为1~3 mm的精度,U方向优于10 mm。
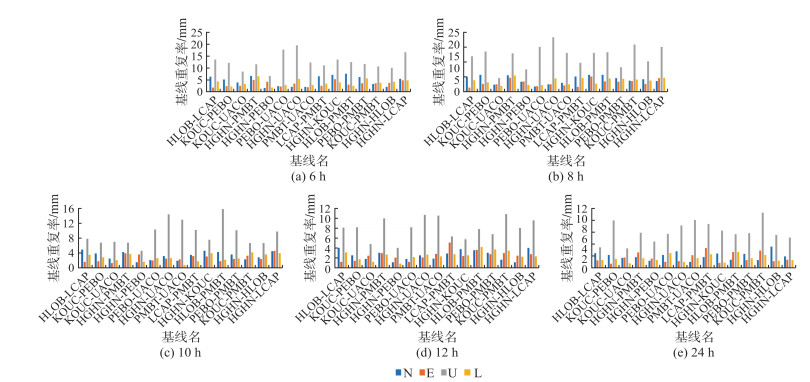 |
| 图 5 中基线6 h、8 h、10 h、12 h、24 h解算各方向基线重复率 Fig.5 The Baseline Repeat Rates of 6 h, 8 h, 10 h, 12 h, 24 h of Medium Baseline |
计算中基线观测6 h、8 h、10 h、12 h与24 h解算的固定误差和比例误差,结果如表 2~表 6所示,可以看出中基线解算的比例误差可以达到10-9~10-8量级的精度,N方向固定误差分别为4.1 mm、3.8mm、3.1 mm、2.3 mm、1.6 mm, E方向固定误差分别为1.8 mm、1.6 mm、1.5 mm、1.4 mm、1.3 mm, U方向固定误差分别为12.2 mm、10.6 mm、8.0mm、6.8 mm、4.9 mm。
| 表 2 观测6 h中基线固定误差及比例误差 Tab.2 Fixed Error and Proportional Error of 6 h of Medium Baseline |
 |
| 表 3 观测8 h中基线固定误差及比例误差 Tab.3 Fixed Error and Proportional Error of 8 h of Medium Baseline |
 |
| 表 4 观测10 h中基线固定误差及比例误差 Tab.4 Fixed Error and Proportional Error of 10 h of Medium Baseline |
 |
| 表 5 观测12 h中基线固定误差及比例误差 Tab.5 Fixed Error and Proportional Error of 12 h of Medium Baseline |
 |
| 表 6 观测24 h中基线固定误差及比例误差 Tab.6 Fixed Error and Proportional Error of 24 h of Medium Baseline |
 |
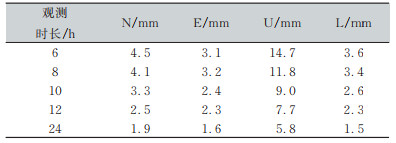
根据表 2~表 6固定误差和比例误差的结果,当基线长度为50 km时,计算不同观测时长在各个方向上的误差如表 7所示。可见,对于50 km长度的基线,解算时长为10 h,即可使3个分量达到毫米级解算精度。
| 表 7 50 km基线不同观测时长在不同方向误差 Tab.7 Error in Different Directions for Different Observation Time of 50 km Baseline |
 |
2.3 短基线
图 6为短基线解算的NRMS值,由图 6可以看出,各时段解算的NRMS值小于0.3,符合高精度解算要求。
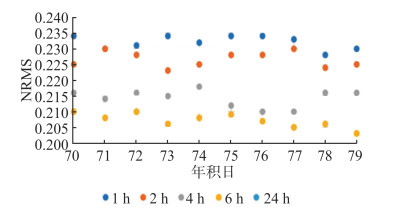 |
| 图 6 短基线NRMS Fig.6 NRMS of Short Baseline |
图 7为短基线1 h、2h、4 h和6 h解算各基线基线重复率。由图 7可以看出,短基线1 h的解算精度,N方向均优于5 mm, E方向约为5~13 mm, U方向约为8~15mm。可见,当观测时长为1 h时,E方向和U方向精度不太稳定。
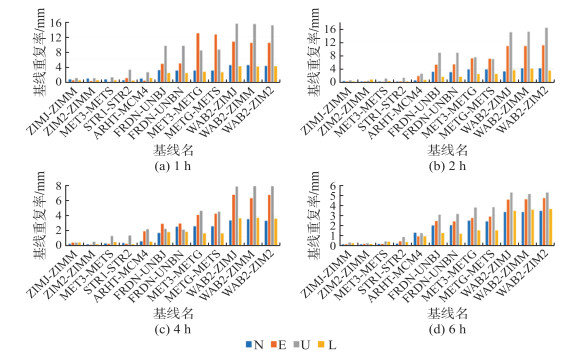 |
| 图 7 短基线1 h、2 h、4 h和6 h解算各方向基线重复率 Fig.7 The Baseline Repeat Rates of 1 h, 2 h, 4 h and 6 h of Short Baseline |
对于长度为1~3 km的5条基线ARHT-MCM4、FRDN-UNBJ、FRDN-UNBN、MET3-METG和METG-METS, 2 h解算精度,N方向均优于4 mm, E方向均优于8 mm, U方向均优于10mm; 4 h解算精度N方向优于3 mm, E方向优于4 mm, U方向优于5 mm; 6 h解算精度,N方向优于3 mm, E方向优于3 mm, U方向优于4 mm。对于长度约为5.2 km的3条基线WAB2-ZIMJ、WAB2-ZIMM、WAB2-ZIM2, 2 h解算精度N方向优于4 mm、E方向优于11 mm、U方向优于16 mm; 4 h解算精度,N方向优于4 mm、E方向优于7 mm、U方向优于8 mm; 6 h解算精度,N方向优于4 mm、E方向优于5 mm、U方向优于6 mm。
进一步地,计算了短基线1 h、2 h、4 h和6 h解算的固定误差和比例误差,结果如表 8~表 11所示。可以看出,短基线解算的比例误差在10-7~10-6量级之间。其中水平方向固定误差分别为1.2 mm、0.7 mm、0.4 mm和0.4 mm,而U方向的固定误差分别为1.6 mm、0.7 mm、0.5 mm和0.6 mm。
| 表 8 观测1 h短基线固定误差及比例误差 Tab.8 Fixed Error and Proportional Error of 1 h of Short Baseline |
 |
| 表 9 观测2 h短基线固定误差及比例误差 Tab.9 Fixed Error and Proportional Error of 2 h of Short Baseline |
 |
| 表 10 观测4 h短基线固定误差及比例误差 Tab.10 Fixed Error and Proportional Error of 4 h of Short Baseline |
 |
| 表 11 观测6 h短基线固定误差及比例误差 Tab.11 Fixed Error and Proportional Error of 6 h of Short Baseline |
 |
根据固定误差和比例误差的情况,当基线长度为5 km时,计算不同观测时长在各个方向上的误差如表 12所示。
| 表 12 5 km基线不同观测时长在不同方向上误差 Tab.12 Error in Different Directions for Different Observation Time of 5 km Baseline |
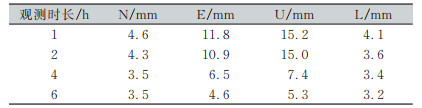 |
由此可见,对于5 km长度的基线,解算时长为4 h,即可使3个分量达到毫米级解算精度。
3 结束语定量分析观测时长对不同长度基线的解算精度的影响,对不同应用场景下解算时长设置和基线选择有较大的帮助。基于GAMIT软件进行静态解算,分析结果表明,对于不同长度的基线,解算精度达到毫米级所需时间不同。对于1 000 km长度的基线,观测时长需要24 h;对于50 km长度的基线,观测时长需要10 h;而对于5 km的基线,4 h的观测时长即可达到优于10 mm的精度。
| [1] |
'92中国GPS会战(A级网)数据处理分析[J]. 武汉测绘科技大学学报, 1995(1): 40-45. |
| [2] |
兰孝奇. GPS精密变形监测数据处理方法及其应用研究[D]. 南京; 河海大学, 2005.
|
| [3] |
林波. GNSS技术在变形监测中的应用[D]. 银川: 宁夏大学, 2016.
|
| [4] |
不同截止高度角对GAMIT基线解算的影响分析[J]. 测绘地理信息, 2017, 42(3): 14-17. |
| [5] |
利用北海CORS监测大气可降水量的应用研究[J]. 测绘地理信息, 2015, 40(5): 36-38. |
| [6] |
利用GAMIT进行高精度GPS基线解算的方法及精度分析[J]. 测绘通报, 2011(8): 5-8. |
| [7] |
利用徕卡GS18仪器进行高精度RTK定位试验与分析[J]. 测绘通报, 2019(4): 155-158. |
| [8] |
GPS形变监测网基线处理中系统误差的分析[J]. 武汉大学学报·信息科学版, 2001, 26(3): 196-199. |
| [9] |
GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005.
|
| [10] |
尚小伟. GNSS多基站变形监测系统技术研究与应用分析[D]. 成都: 西南交通大学, 2018.
|
| [11] |
GAMIT数据处理中基线解算模式的对比分析[J]. 测绘地理信息, 2016, 41(2): 18-21. |
| [12] |
高精度GPS数据处理中GAMIT批处理方法与实现[J]. 测绘信息与工程, 2012, 37(2): 10-12. |
| [13] |
GAMIT在高精度桥梁平面控制网中的应用[J]. 地理空间信息, 2012(2): 79-81. |
| [14] |
基于GAMIT的GPS短基线解类型分析及应用[J]. 测绘通报, 2011(10): 27-29. |
| [15] |
吴海金. 多GNSS实时动态变形监测数据处理方法研究与软件实现[D]. 武汉: 武汉大学, 2018.
|
 2022, Vol. 47
2022, Vol. 47

