| 利用稀疏角度数据改进空间目标TLE轨道预报精度 |
2. 地球空间信息技术协同创新中心,湖北 武汉,430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
自20世纪50年代前苏联首次发射第一颗人造卫星Sputnik-1以来,人类发射航天器探索太空的脚步不断加快,大量的空间碎片也不断产生。然而截至到2016年底,近7 000颗在轨航天器仅有1 400颗仍在继续服役,其余航天器则统统失效从而成为了太空碎片[1, 2]。分布在各自轨道、各自区域的太空碎片共同形成了当今的空间碎片环境。太空正变得愈发拥挤,因此必须具备对已有空间目标进行探测、编目及准确预报的能力。
当前,公众进行空间目标轨道预报主要数据源是双行根数数据(two line elements,TLE),由北美防空联合司令部(North American Aerospace Defense Command,NORAD)维护并每日更新,是目前世界上发布的编目最完善的空间目标轨道数据信息。TLE配合SGP4/SDP4力学模型计算可得到空间目标轨道预报的结果[3]。SGP4/SDP4是一种简化的力模型,它只考虑了地球引力位J2、J3、J4带谐项的影响。利用这种模型可以对计算精度和速度进行较好的折衷[4],同时该模型可以顾及多种摄动因素的影响[5, 6],因此使得TLE预报的精度并不高。有学者对1 120个空间碎片的轨道精度进行了分析,结果表明近地空间碎片预报3 d的误差就已达40 km[7]。许晓丽等[8]分析了动力学模型中地球非球形引力位田谐摄动项对编目轨道精度的影响,发现TLE编目轨道中存在随时间周期变化的系统差,该误差甚至可以达到千米量级。显然这样的精度无法满足空间目标碰撞预警的需求。
在改进TLE预报精度方面,刘卫等[9]利用目标历史TLE数据生成了准观测值数据重新进行了轨道拟合,对多个独立时段拟合后轨道根数结合数值方法的预报误差进行统计,结果表明,拟合后的TLE根数预报精度与稳定性有很大提升。然而对TLE的改善还不够理想。
1 光电阵数据改进TLE原理作为地球轨道空间目标编目数据,TLE虽然具有发布快速,信息全面,易于获得的优点,但其也有较为明显的不足,主要表现在目标轨道预报精度较低,不能满足空间碰撞预警和空间碎片清除等空间态势感知日益提高的精度需求。TLE预报的误差主要由两部分组成。一是由它利用的SGP4/SDP4模型引起的,该模型为了提高计算速度对地球引力场模型等进行了精度上的折衷,是一种简化的动力学模型,在预报的轨道积分过程中引入了误差;二是由确定TLE所用的观测值误差引起的,观测值含有误差使得确定出的轨道根数与实际轨道误差较大。
目前针对空间目标的观测手段主要有光学测角、激光测距和雷达测量3种。在这3种技术中,雷达是当今空间探测跟踪的最强有力的技术,可确定空间目标的方向和距离等信息,但是测量精度不高。
空间碎片激光测距技术(debris laser ranging,DLR)是利用测站向碎片发射激光再接收反射的激光后获得测站至目标距离的一种技术手段,起源于卫星激光测距技术(satellite laser ranging,SLR),是当前精度最高的空间目标轨道测量手段。但DLR也有较明显的短板,例如:激光打在有高速旋转的空间碎片上面后将向四周反射,从而只有很小部分能被测站接收,由此需要更强的激光能量,通常是SLR技术的数千倍。此外,空间碎片的预报轨道通常由TLE提供,精度低,误差大,一般需要有实时精密定轨技术支持才能准确地引导激光束指向碎片,从而缩短了激光测距的跟踪观测时段。这些原因导致DLR的观测数据非常稀疏。
光学角度观测是利用光学摄影技术,直接或间接地利用恒星的位置来确定观测目标的角度观测值。空间目标自身并不发光,但通过反射太阳光可以使光学望远镜CCD探测到信息,且一般而言测角精度可达1~2″。相较于激光测距技术,光学角度观测功耗低,易实现,可获得更充足的数据。而且有研究表明[11],利用基于单站的间隔约24 h的两次精密测角通过数据定轨时,1~2 d的轨道预报精度可优于20″。
利用TLE进行轨道预报时必须同时使用SGP4/SDP4模型,即使将TLE代入更精确的摄动力模型甚至是数值积分器中也不会提高预报的精度[12]。尽管TLE的定义及其匹配的SGP4/SDP4模型明确,但从观测值产生TLE的具体算法从未公布。考虑当今的计算能力,直接利用数值积分和精密摄动力模型进行轨道解算和预报,并在此基础上生成TLE,可能是一种更好的方法。它既保留了TLE/SGP4在数据传播和计算速度上的优点,同时还具有较高的轨道预报精度。
图 1阐释了利用该方法处理长春光电阵角度观测数据改进TLE的流程:首先利用t0~t2共3 d的长春光电阵数据(“·”点)对目标进行精密定轨并预报至t3,产生共10 d的轨道数据。将3 d定轨时段内最后一组TLE数据的参考历元时刻作为待改进的新TLE的参考历元(图中t1时刻),把t1时刻TLE轨道根数设为待估参数X0,而将t0~t3时段内由精密定轨和预报获得的轨道位置作为观测值Yobs(“×”点),可得到观测方程:
| $ {\mathit{\boldsymbol{Y}}_{{\rm{obs}}}} = \mathit{\boldsymbol{H}}\left( {X, {\rm{ }}t} \right) + \mathit{\boldsymbol{V}} $ | (1) |
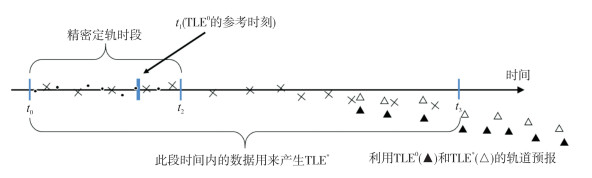 |
| 图 1 光电阵数据改进TLE原理 Fig.1 Process of Improving TLE Data by Using Telescope-Array Observations |
将该式线性化后可得到用以改进TLE的最小二乘估计的基本方程:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\tilde B}}{x_0} + \mathit{\boldsymbol{V}} $ | (2) |
式中,x0是待估参数的改正值;
利用上述模型进行迭代计算,最终得到改进的目标双行根数TLE*。图 1的“▲”点表示利用未改进的TLE在SGP4摄动模型下,从t1时刻对目标预报近7 d之后的轨道与实际轨道的偏差;同样地,“△”点表示改进后的TLE对目标的预报偏差(图 1中只标记了7 d轨道预报中靠后时段对应的黑、白三角形点以使图示简洁)。两者的对比显示:利用t0~t3时段的数据改进后,TLE*预报偏差要好于未改进的TLE0所预报的偏差。
2 实验设计长春光电阵在晴朗的夜晚可观测获得超过1 000个NORAD编目目标的观测弧段数据,其数据精度优于9 as[14]。然而在连续3 d时间内,不同目标的观测弧段数量并不相同。因此利用稀疏角度数据分析不同条件下TLE改进效果是本文的主要研究内容。
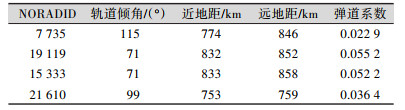
本文选择了4个NORAD编目库中的目标作为实验对象,表 1为目标信息,本文同时获得了2017年9月1日—30日的TLE数据,这些TLE数据都是通过space-track(www.space-track.org)网站获取的。实验同时也获得了长春人卫观测站的光电阵数据,时间分布同样在2017年9月1日—30日。本文对每个目标进行了14组分析,即从2017年9月1日—14日起每3 d作为一个算例。
| 表 1 实验选用的NORAD目标信息 Tab.1 Main Parameters of Selected NORAD Objects |
 |
在每个算例中,首先利用3 d的长春光电阵数据对目标进行精密定轨。本文选取的目标在任意3 d内的观测弧段一般是2段或3段,也存在极个别4段以上或仅有1段的情况。
利用TLE0和TLE*分别预报7 d,然后将预报轨道与实际轨道进行比较,可得到新旧两组TLE数据的预报位置误差。
3 实验结果图 2和图 3以箱型图的形式展示了实验的结果。箱型图是对应目标在相应观测条件下所有算例的TLE0和预报位置误差数列的图形化。
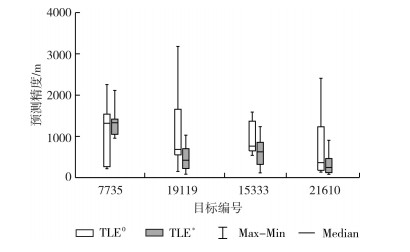 |
| 图 2 各目标3 d内观测弧段数不少于2个时7 d轨道预报误差 Fig.2 7-Day Orbit Prediction Errors Using the Original and Improved TLEs when There are at Least 2 Observed arcs within 3 days |
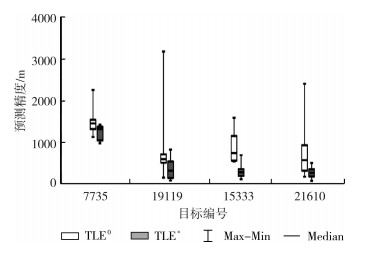 |
| 图 3 各目标3 d内观测弧段数不少于3个时7 d轨道预报误差 Fig.3 7-Day Orbit Prediction Errors Using the Original and Improved TLEs when There are at Least 3 Observed arcs within 3 days |
图 2给出4个目标在3 d内的观测弧段不少于2个时,使用原始TLE0与改进后TLE*预报轨道7 d后得到的预报位置误差箱型图。可以看出除7735号目标外,其余3个目标改进后的TLE*的预报精度都优于原始TLE0的预报结果。7735号目标改进后TLE*的预报位置误差最小值和1/4分位值均比原始TLE0预报误差大,表明部分改进后的TLE*其预报精度有所降低。这主要是因为该目标在3 d的定轨时间内,14个算例中其中7个算例仅有两个观测弧段,导致定轨及预报的精度不高,从而不能有效改善TLE精度。
图 3是4个目标在3 d定轨时段内的观测弧段数不少于3个时TLE0和TLE*预报位置误差箱型图,该组实验剔除了仅包含2个观测弧段的算例的计算结果。可以看到,TLE*显著优于TLE0,且所有目标TLE*预报误差相较于图 1都大幅下降,且预报7 d平均误差在200 m左右,误差最大值控制在1 000 m附近。而TLE0预报精度在700 m以上,部分误差则达到2 000~3 000 m。该组实验仅有一个算例的TLE*预报精度未能优于TLE0,其预报误差分别是351.8 m和317.5 m。出现这种情况原因可能是原有的TLE其自身精度已经比较好。因此,根据实验结果,当3 d内至少有3个弧段观测数据时,绝大部分目标利用本文提出的方法改进TLE*可较原始TLE0提高近50%的位置预报精度。
图 4是19119号目标利用2017年9月14日—16日数据改进TLE后,TLE0和TLE*预报7 d的位置误差变化情况,该算例在3 d内包含了3个观测弧段。此处两种TLE的轨道预报方法相同,采用SGP4摄动模型通过轨道积分进行预报。可以看出,TLE*在预报的各时段都比TLE0要好,未改进的TLE0预报误差1 d已达707.9 m,到第7天时更是达到1 233.1 m,而改进的TLE*在7 d内的预报误差都在200 m以内,预报7 d后的位置误差仅有67.4 m。且改进的TLE*的位置预报误差更加平滑,相比之下原有TLE0的预报误差在第7天时存在大幅跃升,这也反应了现有TLE数据预报误差的一个特性。
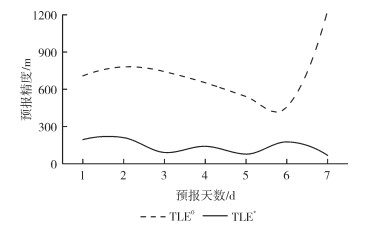 |
| 图 4 19119号目标预报7 d的位置误差 Fig.4 Orbit Prediction Result of Object 19119 by TLE0 and in 7 days |
4 结束语
本文针对TLE预报精度不高的问题,提出了利用稀疏光学角度数据改进TLE的方法。具体通过给定每个目标前后跨度3 d的地面站光学角度数据进行精密定轨,然后利用精密定轨的结果进行轨道外推,获得前后跨度共10 d的轨道来改进TLE,最后分别利用改进的TLE*和原始的TLE0进行轨道预报并评估预报误差。结果表明:当3 d定轨时段内含有不少于3个观测弧段时,95%的目标的改进后TLE*预报位置误差降幅达50%,且预报7 d的最大位置误差在1 km附近。本文认为,利用光学测角数据对目标TLE进行改进,可以使轨道预报精度得到显著提高。
| [1] |
李彬. 空间碎片快速精密轨道确定与预报若干关键问题研究[D]. 武汉: 武汉大学, 2017
|
| [2] |
刘磊, 桑吉章, 雷祥旭, 等. 空间碎片环境动态可视化软件开发[J]. 测绘地理信息, 2019, 44(5): 87-91. |
| [3] |
陈俊宇, 李彬, 陈立娟, 等. 联合多个两行根数进行轨道预报[J]. 红外与激光工程, 2016, 45(S2): 35-39. |
| [4] |
韩蕾, 陈磊, 周伯昭. SDP4/SGP4模型用于空间碎片轨道预测的精度分析[J]. 中国空间科学技术, 2004(8): 65-71. |
| [5] |
李骏, 吴京, 安玮, 等. 面向天基光学监视的空间目标TLE拟合与跟踪方法[J]. 电子学报, 2009, 37(11): 2 463-2 469. |
| [6] |
赵朋, 花向红, 赵磊磊, 等. 北斗卫星钟差频间偏差及对定位精度影响分析[J]. 测绘地理信息, 2019, 44(1): 27-31. |
| [7] |
韦栋, 赵长印. SGP4/SDP4模型精度分析[J]. 天文学报, 2009, 50(3): 332-339. DOI:10.3321/j.issn:0001-5245.2009.03.010 |
| [8] |
许晓丽, 熊永清. 双行根数编目体系轨道误差研究[J]. 天文学报, 2018, 59(3): 31-38. |
| [9] |
刘卫, 王荣兰, 刘四清, 等. TLE预报精度改进及碰撞预警中的应用[J]. 空间科学学报, 2014, 34(4): 449-459. |
| [10] |
雷祥旭, 桑吉章, 李振伟. LEO空间目标地基甚短弧角度数据初轨确定[J]. 测绘地理信息, 2019, 44(2): 71-73. |
| [11] |
Sang J Z, Bennett J C, Smith C. Experimental Results of Debris Orbit Predictions Using Sparse Tracking Data from Mt. Stromlo[J]. Acta Astronautica, 2014, 102: 258-268. DOI:10.1016/j.actaastro.2014.06.012 |
| [12] |
白显宗, 陈磊, 张翼, 等. 空间目标碰撞预警技术研究综述[J]. 宇航学报, 2013, 34(8): 1 027-1 039. |
| [13] |
刘林. 航天器定轨理论与应用[M]. 北京: 电子工业出版社, 2015.
|
| [14] |
雷祥旭, 桑吉章, 李振伟. 长春地基光电阵观测数据初步分析[J]. 测绘地理信息, 2019, 44(1): 41-44. |
 2021, Vol. 46
2021, Vol. 46

