| 一种双目直接法视觉里程计 |
近十年来机器人技术得到了突飞猛进的发展,生产生活的各个领域都出现了机器人技术的身影,如机械制造、仓储管理、智能家居、室内场景三维建模、智慧城市等。机器人通过感知周围环境,构建局部地图并确定自身的位置,实现自主运动,这种技术被称作同时定位与制图(simultaneous localization and mapping, SLAM)。视觉里程计(visual odometry, VO)是同时定位与制图的重要组成部分,是使用视觉传感器连续采集的影像估计机器人运动轨迹的关键技术。车载测绘系统使用GNSS(global navigation satellite system)对车辆进行定位,但城市环境下,GNSS通视条件较差,需融合IMU(inertial measurement unit)等其他传感器进行辅助定位[1]。视觉里程计相比IMU测量具有漂移小的优点,能够进行更长时间的精确测量,与GNSS结合可获得高频率、高精度的定位结果。视觉里程计可在定位的同时构建周围环境简易地图,辅助车载激光雷达提取三维建筑立面[2]。
视觉里程计通常分为直接法与特征点法两类主要实现方法。直接法视觉里程计在影像上选取若干像素,通过最小化不同影像之间同名像素点的光度误差,实现影像位置姿态的求解,常见的直接法视觉里程计包括DTAM(dense tracking and mapping)[3]、SVO(semidirect visual odometry)[4]、LSD-SLAM(large-scale direct SLAM)[5]、DSO(direct sparse odometry)[6]等。特征点法视觉里程计在影像上提取特征点并计算特征点描述子,通过最小化不同影像之间同名特征点的重投影误差,解算影像的位置姿态。常见的特征点法视觉里程计有PTAM(parallel tracking and mapping)[7]、ORB-SLAM2[8]等。
直接法视觉里程计相较于特征点法视觉里程计,无需提取特征点与计算描述子,所以处理速度优于特征点法视觉里程计,同时使用丰富的影像信息,结果更加鲁棒。且直接法视觉里程计可构建稠密地图,拥有更广泛的应用领域。
双目相机已知基线,可通过匹配获得场景深度。在视觉里程计领域,双目相机解决了单目相机尺度漂移的问题,适合长时间、大范围稳定工作。当前,使用双目相机的视觉里程计有ORB-SLAM2[8]、Stereo LSD-SLAM[9]。ORB-SLAM2属于特征点法,对角点稀少的场景适应能力差。Stereo LSD-SLAM属于直接法,但其光度误差模型没有考虑多帧影像之间的光照差异,对光照变化敏感。
本文基于DSO[6]框架,提出了一种使用双目相机的直接法视觉里程计,充分利用双目影像已知基线的优势,对视觉里程计的关键帧跟踪、局部窗口优化进行约束,改善轨迹位姿漂移问题。相对于特征点法的ORB-SLAM2,在角点稀少的场景中能获得精确的跟踪结果;相对于直接法的Stereo LSD-SLAM,将光照变化纳入光度误差模型,结果更加鲁棒。
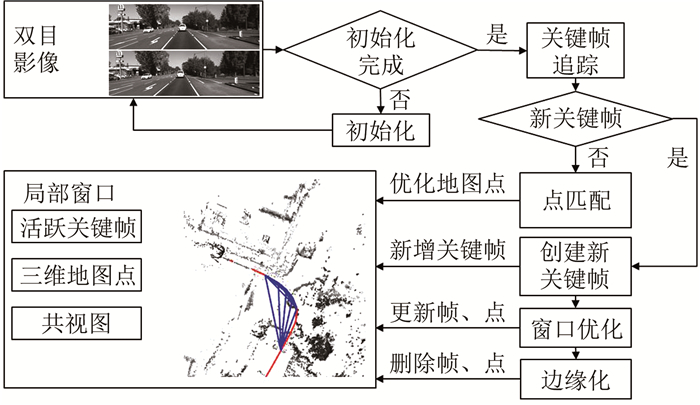
1 双目直接法视觉里程计 1.1 算法流程本文提出的直接法视觉里程计算法流程如图 1所示,包括初始化、关键帧追踪、窗口优化过程。
 |
| 图 1 本文算法流程图 Fig.1 Flow Chart of Algorithm |
系统在首次接收双目影像时,将双目影像进行核线匹配生成三维地图点,并将这一组双目影像作为关键帧加入局部窗口完成初始化流程。系统初始化完成后,当新的双目影像输入系统时,将上一关键帧的地图点投影到当前影像,通过最小化光度误差求解两者之间的相对位姿。在获得新双目影像位姿后,判断是否需要生成新的关键帧。如果需要,则将新双目影像作为关键帧加入到局部窗口中,与其他关键帧的位姿、相机的内参数、地图点的深度进行联合优化。若不需要,则用其对局部窗口中关键帧的地图点深度进行优化。
当局部窗口中的关键帧数量大于给定阈值时,使用边缘化策略将与其他关键帧共视条件最差的关键帧及其地图点从局部窗口中移除。边缘化策略将被移除变量信息保留在局部窗口中,防止其他关键帧位姿向错误方向漂移。
本文的特色是充分利用双目影像已知基线的优势,将双目影像对与时序影像对的光度误差一同作为优化目标,用强约束保证相机位姿正确求解。
1.2 光度误差直接法视觉里程计通过最小化光度误差,求解影像之间的相对位姿。光度误差计算方法是直接法视觉里程计的核心,一个鲁棒的光度误差计算方法能够保证直接法视觉里程计相对位姿正确求解。本节介绍算法使用的光度误差计算方法。
假设在i影像上能被j影像观察到的点集为Pi,两张影像之间的光度误差可以表示为:
| $ E_{j i}=\sum\limits_{\boldsymbol{p} \in P_{i}} \omega_{\boldsymbol{p}}\left\|I_{j}\left[\boldsymbol{p}^{\prime}\right]-I_{i}[\boldsymbol{p}]\right\|_{\gamma} $ | (1) |
式中, Ii、Ij分别表示在i影像和j影像上的灰度值;
| $ \omega_{\boldsymbol{p}}=\frac{c^{2}}{c^{2}+\left\|\nabla I_{i}[\boldsymbol{p}]\right\|_{2}^{2}} $ | (2) |
式中,c为一常数,防止梯度接近于0时加权系数过大;p′是p点在j影像上的对应点。使用两张影像之间的相对位姿将p点投影至j影像上获得p′点坐标,公式为:
| $ \boldsymbol{p}^{\prime}=\boldsymbol{K} \rho_{j}\left(\boldsymbol{R}_{j i} \boldsymbol{K}^{-1} \rho_{i}^{-1} \boldsymbol{p}+\boldsymbol{t}_{j i}\right) $ | (3) |
式中,K是相机的内参矩阵;ρi、ρj分别是p在i影像和j影像的逆深度;Rji、tji是两张影像之间的相对位姿。
光度误差直接计算影像之间的灰度差值,容易受到光照、相机曝光变化的影响。为了减弱这种影响,在不同影像像素值之间添加仿射变换参数a、b,用于拟合光照变化对影像像素值的影响。并且使用每个点与其周围点一同计算光度误差,即Pi中的点p扩展为Np。最终得到两张影像之间鲁棒的光度误差计算方法如:
| $ {E_{ji}} = \sum\limits_{\mathit{\boldsymbol{p}} \in {P_i}\mathit{\boldsymbol{\widetilde p}} \in {N_\mathit{\boldsymbol{p}}}} {{\omega _{\mathit{\boldsymbol{\widetilde p}}}}} {\left\| {{I_j}\left[ {\mathit{\boldsymbol{\widetilde p}}{\rm{'}}} \right] - {b_j} - \frac{{{e^{{a_j}}}}}{{{e^{{a_i}}}}}\left( {{I_i}\left[ {\mathit{\boldsymbol{\widetilde p}}} \right] - {b_i}} \right)} \right\|_\gamma } $ | (4) |
式中,使用自然指数进行仿射变换,可防止优化过程中系数变为负数破坏优化目标。
1.3 点与帧的管理为保证优化的实时性,在运行过程中保留固定数量的关键帧用于局部窗口优化。每个关键帧包含与其联系的地图点,这些地图点用于约束关键帧之间的相对位姿关系。关键帧i的状态可使用向量[ξi, ai, bi]T表示,其中ξi为该帧在世界坐标系下位姿,[ai, bi]T是该帧光度仿射变换参数,用于不同帧之间像素值的转换。
局部窗口中的每一个地图点都有一个主关键帧,地图点在空间中的三维位置可以用向量[u, v, ρ]T表示,其中[u, v]T是该点在主关键帧影像上的像素坐标,ρ是相对于主关键帧影像的逆深度。
在有新的关键帧生成时,算法将新关键帧左影像中高梯度值的像素作为追踪点,并使用归一化交叉相关系数(normalized cross correlation, NCC)在右影像核线上搜索匹配点,得到匹配点坐标后,即可计算待追踪点的逆深度,计算公式为:
| $ \rho=\frac{u_{L}-u_{R}}{b} $ | (5) |
式中,b为左右影像的基线长度;uL、uR分别为匹配点在左右影像上的u坐标。
本文算法提取固定数量的高梯度值像素作为待追踪点,有利于控制系统的计算量,且不会大幅降低相机跟踪精度。因为直接法视觉里程计解空间具有较多局部最优点[10],使用双目影像初始化待追踪点的逆深度,有利于系统收敛于全局最优点,得到正确的优化结果。并且初始化待追踪点可以加速系统收敛,提高系统实时性。通过归一化交叉相关系数进行核线匹配,可在左右影像曝光效果差异较大时获得鲁棒的匹配结果。
1.4 关键帧追踪在输入新影像之后,通过匀速运动模型假设,获得其与最新关键帧的初始相对位姿。随后将其与最新关键帧进行匹配,优化两者间的相对位姿。如果环境光照变化过大,则新影像会被用于生成新关键帧,并加入到局部窗口优化过程中,以进一步优化当前影像位姿。否则用新影像优化窗口中所有关键帧的深度。
新影像与关键帧之间的匹配使用§1.2节中提到的方法计算光度误差,通过最小化光度误差得到初始的位姿。在单目直接法的基础上,计算新双目左右影像之间的光度误差,联合关键帧与新影像的光度误差一同优化,计算公式为:
| $ \begin{array}{*{20}{c}} {{E_{ji}} = }\\ {\sum\limits_{\boldsymbol{p} \in {P_i}\mathit{\boldsymbol{\tilde p}} \in {N_\mathit{\boldsymbol{p}}}} {{\omega _{\mathit{\boldsymbol{\tilde p}}}}} \left( {{{\left\| {{I_j}\left[ {{{\mathit{\boldsymbol{\widetilde p}}}^\prime }} \right] - {b_j} - \frac{{{e^{{a_j}}}}}{{{e^{{a_i}}}}}\left( {{I_i}[\mathit{\boldsymbol{\widetilde p}}] - {b_i}} \right)} \right\|}_\gamma } + } \right.}\\ {\left. {{{\left\| {{I_R}\left[ {{{\mathit{\boldsymbol{\widetilde p}}}_R}} \right] - {b_R} - \frac{{{e^{{a_R}}}}}{{{e^{{a_i}}}}}\left( {{I_i}[\mathit{\boldsymbol{\widetilde p}}] - {b_i}} \right)} \right\|}_\gamma }} \right)} \end{array} $ | (6) |
本文方法利用双目相机已知基线的优势,对优化目标进行了约束,确保优化结果不会发生尺度漂移。
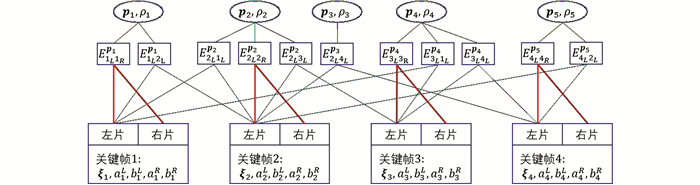
1.5 窗口优化窗口优化从关键帧追踪流程获得带有初始位姿的新关键帧,将新关键帧与窗口中其他关键帧进行联合优化。优化的目标参数是窗口中所有关键帧的位姿、光度变换参数、相机的内参数、三维点的逆深度。采用高斯牛顿方法最小化整体误差,获得最优的定位效果。联合优化的因子图如图 2所示。
 |
| 图 2 窗口优化因子图 Fig.2 Factor Graph of Windowed Optimization |
本文创造性地将双目左右影像之间的光度误差纳入到优化过程中,实现对逆深度的强约束,缓解尺度漂移。相关光度误差约束在窗口优化因子图中用粗线表示。
为保证优化的实时性,在运行过程中保留固定数量的关键帧用于局部窗口优化,对比实验保留8个关键帧。
为保证系统实时运行,需控制窗口关键帧的数量。当有新关键帧加入时,将窗口中观察到其他帧地图点最少的帧剔除。剔除过程中使用边缘化策略将被剔除帧、点的信息保留在窗口中,防止窗口中其他帧发生漂移。
边缘化策略为:
| $ \left\{\begin{array}{l} {\left[\begin{array}{ll} \boldsymbol{H}_{\alpha \alpha} & \boldsymbol{H}_{\alpha \beta} \\ \boldsymbol{H}_{\beta \alpha} & \boldsymbol{H}_{\beta} \end{array}\right]\left[\begin{array}{c} \boldsymbol{x}_{\alpha} \\ \boldsymbol{x}_{\beta} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{b}_{\alpha} \\ \boldsymbol{b}_{\beta} \end{array}\right]} \\ \left(\boldsymbol{H}_{\beta}-\boldsymbol{H}_{\beta \alpha} \boldsymbol{H}_{\alpha \alpha}^{-1} \boldsymbol{H}_{\alpha \beta}\right) \boldsymbol{x}_{\beta}=\boldsymbol{b}_{\beta}-\boldsymbol{H}_{\beta x} \boldsymbol{H}_{\alpha \alpha}^{-1} \boldsymbol{b}_{\alpha} \\ \hat{\boldsymbol{H}}_{\beta \beta} \boldsymbol{x}_{\beta}=\hat{\boldsymbol{b}}_{\beta} \end{array}\right. $ | (7) |
式中,xα、xβ分别表示被边缘化的参数和保留在窗口中的参数。xα的信息Hαα-1,以及xα、xβ之间的相互信息Hαβ被保留在边缘化之后的窗口信息
使用KITTI数据集[11]对算法效果进行实验验证。KITTI数据集由德国卡尔斯鲁厄理工学院和丰田美国技术研究院联合采集,是世界范围内最大的道路环境计算机视觉算法评估数据集。该数据集使用激光数据与GPS数据测量了汽车运动轨迹,作为真实轨迹对算法性能进行评估。
该数据集共有11条具有真实轨迹的道路数据,覆盖市区、乡村、高速公路等多种真实应用环境,场景中含有各类型运动目标,如行人、自行车、摩托车、汽车等。该数据集双目相机的基线长度为0.53 m,可测量较远距离点的深度。部分数据的双目影像截图如图 3所示。
 |
| 图 3 KITTI双目数据集部分影像 Fig.3 Part of KITTI Stereo Dataset |
选取ORB-SLAM2[8]作为对比算法,去除回环检测和重定位功能的ORB-SLAM2退化为特征点法视觉里程计,能够与本文的直接法视觉里程计形成对比实验。ORB-SLAM2是当前特征点法SLAM中较成熟的方法,在视觉里程计部分采用了逆深度、局部窗口优化等多种策略,适应公路、室内等多种应用环境。ORB-SLAM2在每张影像上提取角点作为特征点,并计算特征点描述子,通过描述子匹配不同影像之间的特征点,实现影像位姿的求解。但对于角点缺乏的场景,ORB-SLAM2提取的特征点有限,相机相对位姿计算不够鲁棒。本文方法可从线段上提取追踪点,能很好适应角点缺乏而线段丰富的场景。
2.2 实验结果选取KITTI数据集中具有代表性的5条道路数据,将本文方法与ORB-SLAM2进行对比实验。并依据数据集提供的真实轨迹数据,计算本文方法与ORB-SLAM2方法所得轨迹数据与真实轨迹数据的绝对位移误差的最大值MAX和均方根误差RMSE,作为定量评价指标。这两项指标越小,算法估计结果越准确,实验结果的统计表格如表 1所示。
| 表 1 对比实验误差统计表格 Tab.1 Statistics of Two Algorithms |
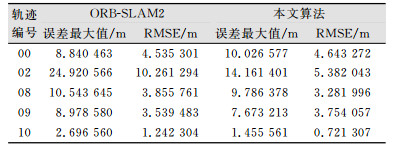 |
从表格中可以看出在02、10数据上,本文算法对ORB-SLAM2有明显优势。02数据存在大量行道树,纹理重复,ORB-SLAM2的特征点法容易匹配到错误的特征点对,而本文的直接法利用多张影像的深度对待求点的深度做预先估计,缩小核线影像的搜索范围,能够得到正确匹配点对。02数据的两种方法所得结果与真实轨迹对比如图 4所示。
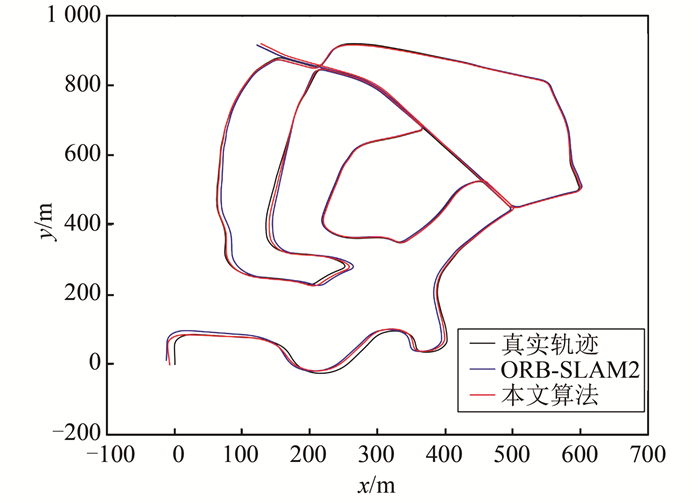 |
| 图 4 KITTI02数据结果对比图 Fig.4 Trajectories Compare on KITTI 02 |
另一方面,本文方法提取的追踪点数量远大于ORB-SLAM2提取的追踪点,相机位姿追踪更加鲁棒。本方法将高梯度值像素点作为追踪点,计算影像的相对位姿,不要求追踪点在图像中必须是角点,所以可充分利用人工环境中普遍存在的线段,这些线段包括公路标记线、房屋、指示牌,甚至是公路周围房屋投影在路面上的阴影。图 5是ORB-SLAM2与本文方法在同一张影像上提取追踪点的对比图,其中,图 5(a)用绿色方框标示的是ORB-SLAM2提取的追踪点,共有469个;图 5(b)用彩色方块标示的是本文方法提取的追踪点,共有14 746个。可以看到本文方法在影像中的房屋结构线段与阴影边缘都提取了大量的追踪点,而ORB-SLAM2只能在角点处提取追踪点,数量远少于本文方法。在车载道路环境,影像中竖直线段有利于追踪汽车转向,水平线段有利于追踪汽车位移,所以本文方法优于ORB-SLAM2。
 |
| 图 5 追踪点提取对比图 Fig.5 Tracking Points Compare |
3 结束语
直接法视觉里程计是当前计算机视觉的热门研究点,尚处于起步阶段。本文提出的基于双目视觉的直接法视觉里程计,使用了鲁棒的光度误差计算方法,将双目影像光度误差与时序影像光度误差联合优化,在车载道路数据上取得了良好的测试结果。以均方根误差为定量评价标准,本文方法精度与当前较优秀的特征点法视觉里程计ORB-SLAM2相当,在纹理重复或线段丰富区域效果优于ORB-SLAM2。但本文方法关键帧追踪流程中的匀速运动模型假设不能很好拟合剧烈的相机运动,优化迭代次数多,实时性受到影响。针对此问题,后续将研究使用其他传感器(如IMU)辅助提供更合理的关键帧追踪初始值。相信随着车载测绘技术的普及,直接法视觉里程计将在测绘领域拥有更广泛应用。
| [1] |
郭强, 尹业宏, 宣扬. 超紧组合中不同精度IMU对GNSS信号跟踪性能的提升[J]. 测绘地理信息, 2016, 41(6): 9-11. |
| [2] |
龚健雅, 崔婷婷, 单杰, 等. 利用车载移动测量数据的建筑物立面建模方法[J]. 武汉大学学报·信息科学版, 2015, 40(9): 1137-1143. |
| [3] |
Newcombe R A, Lovegrove S J, Davison A J. DTAM: Dense Tracking and Mapping in Real-Time[C]. IEEE International Conference on Computer Vision, Barcelona, Spain, 2011
|
| [4] |
Forster C, Zhang Z, Gassner M, et al. SVO: Semidirect Visual Odometry for Monocular and Multi-Camera Systems[J]. IEEE Transactions on Robotics, 2017, 33(2): 249-265. DOI:10.1109/TRO.2016.2623335 |
| [5] |
Engel J, Schöps T, Cremers D. LSD-SLAM: Large-Scale Direct Monocular SLAM[C]. European Conference on Computer Vision, Zurich, Swiss, 2014
|
| [6] |
Engel J, Koltun V, Cremers D. Direct Sparse Odometry[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 40(3): 611-625. |
| [7] |
Klein G, Murray D. Parallel Tracking and Mapping for Small AR Workspaces[C]. Mixed and Augmented Reality, Nara, Japan, 2007
|
| [8] |
Mur-Artal R, Tardós J D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo and RGB-D Cameras[J]. IEEE Transactions on Robotics, 2015, 33(5): 1255-1262. |
| [9] |
Engel J, Stückler J, Cremers D. Large-Scale Direct SLAM with Stereo Cameras[C]. International Conference on Intelligent Robots and Systems, Hamburg, Germany, 2015
|
| [10] |
Engel J, Sturm J, Cremers D. Semi-Dense Visual Odometry for a Monocular Camera[C]. IEEE International Conference on Computer Vision, Sydney, Australia, 2013
|
| [11] |
Geiger A, Lenz P, Urtasun R. Are We Ready for Autonomous Driving? The KITTI Vision Benchmark Suite[C]. IEEE Conference on Computer Vision and Pattern Recognition, Rhode Island, USA, 2012
|
 2020, Vol. 45
2020, Vol. 45

