| 路径计算中的阻力因子分析 |
2. 武汉大学地理信息系统教育部重点实验室,湖北 武汉, 430079
2. Key Laboratory of Geographic Information System, Ministry of Education, Wuhan University, Wuhan 430079, China
目前,在路径计算中所运用的基本方法为基于网络的拓扑分析方法,很少有考虑到阻力因子的研究。分析阻力因子的文章中,对路径计算中的阻力因子分析存在的问题是缺少一套全面有效的综合分析评价体系。
大部分研究着重讨论一个或多个阻力因子对道路交通的影响[1-10]。如果要在阻力因子分析中建立全面的评价体系,要考虑到道路情况、天气情况、时间变化情况、交通规则情况、周围环境5大方面的因素,其涉及的因素众多、关系复杂,且很多因素难以定量化描述,会给评价带来困难,而且评价体系也应当适用于实际的路径计算。应当考虑到哪些因素无法被纳入层次分析法的计算,并在路径计算的过程中将这些因素纳入考虑。所以需要设计出一套合适的路径计算方法。
本文借助层次分析法对阻力因子进行了综合评判,并且针对一些特殊的阻力因子设计路径计算方法,把各种阻力因子与路径计算成功地结合起来,对以后需要考虑多种因素的路径计算方法设计有很大的借鉴意义。
1 基本方法 1.1 层次分析法基本流程运用层次分析法构造系统模型时,大体可以分为以下4个步骤:
1) 建立层次结构模型。应用层次分析法进行综合评判决策时,首先要建立层次结构模型。层次结构模型是层次分析法的关键,它建立在对评价方案充分了解的基础上。根据问题的内部因果,将决策的目标、考虑的因素 (决策准则) 和决策对象按它们之间的相互关系分为目标层、中间层和方案层,绘出层次结构图。在建立层次结构图后,可以根据它生成一张二维表,称为方案因素决策表。该表中数据称为因素数据,记录了待选方案关于各决策因素的信息。
2) 构造判断矩阵。建立了层次结构图与方案因素决策表以后,需要根据决策表中的数据求得各方案关于最底层数据的方案权重,层次分析法采用相对评价方法对方案进行两两比较。如果有n个比较量,则让每一个量与其他量分别进行n-1次两两比较,第i个量与第j个量的比较结果记为aij,再加上与自身的比较结果aii,可形成一个n×n的方阵,称为判断矩阵。判断矩阵的元素aij可以用Satty的1~9标度方法给出,标度方法如表 1所示。
| 表 1 1~9标度法打分规则 Table 1 1-9 Scaling Rules |
 |
3) 层次单排序及其一致性检验。对应于判断矩阵最大特征根λmax的特征向量,经归一化 (使向量中各元素之和等于1) 后记为ω。ω的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。对于一个判断矩阵A,其层次单排序步骤为:① 对A矩阵的每一列归一化处理,得到矩阵B; ② 对矩阵B的每一个行向量求和,并且进行归一化处理,得到A的近似特征向量W;③ 求最大特征值近似值,由AW=λW,求得λ的值。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对判断矩阵确定不一致的允许范围。首先计算矩阵的一致性指标CI (consistency index):
| $ {\rm{CI}} = \frac{{\lambda-n}}{{n-1}} $ | (1) |
式中,λ为矩阵的最大特征根;n为矩阵的阶数。当CI=0时,矩阵有完全的一致性;CI接近于0时,矩阵有满意的一致性;CI越大,矩阵的不一致性越严重。为衡量CI的大小,引入随机一致性指标RI (random index)。RI的取值规则如表 2所示,其中n为矩阵阶数。
| 表 2 随机一致性指标RI Table 2 Random Consistency Index |
 |
接下来,定义矩阵的一致性比率CR (consistency ratio):
| $ {\rm{CR = CI/RI}} $ | (2) |
若CR < 0.1,则认为有满意的一致性,否则需要调整判断矩阵的元素取值。1阶和2阶的判断矩阵具有完全一致性,RI值为0,不需计算。如果判断矩阵通过了一致性检验,那么可用其归一化特征向量作为权向量。
4) 层次总排序及其一致性检验。计算某一层次所有因素对于最高层 (总目标) 相对重要性的权值,称为层次总排序。这一过程是从最高层次到最低层次依次进行的。
假设某决策模型的层次结构图中,B层为A层的下一层,A层m个因素A1、A2、…、Am对总目标的排序为a1、a2、…、am,B层n个因素对上层A中Aj的层次单排序为B1j、B2j、…、Bmj(j=1, 2, …, m)。那么,B层第i个因素对总目标的权值为
同时,还要进行层次总排序的一致性检验,这个过程也是由最高层次到最低层次依次进行的。假设某决策模型的层次结构图中,B层为A层的下一层且为最底层,A层m个因素,B层n个因素;设B层b1、b2、…、bn对A层中因素Aj(j=1,2,…,m) 的层次单排序一致性指标为RIj,随机一致性指标为RIj,则层次总排序的一致性比率为:
| $ {\rm{CR}} = \frac{{{a_1}{\rm{C}}{{\rm{I}}_1} + {a_2}{\rm{C}}{{\rm{I}}_2} + \cdots + {a_m}{\rm{C}}{{\rm{I}}_m}}}{{{a_1}{\rm{R}}{{\rm{I}}_1} + {a_2}{\rm{R}}{{\rm{I}}_2} + \cdots + {a_m}{\rm{R}}{{\rm{I}}_m}}} $ | (3) |
同样,若CR < 0.1,认为层次总排序通过一致性检验,具有满意的一致性,否则需要重新调整那些一致性比率高的判断矩阵的元素取值。
1.2 指标定量评价的方法在确定权重之后,需要对决策中的每一个因子进行评判。在一个包含多项评价指标的体系中,各指标的量纲数值范围各不相同,为了得到一个恰当的综合评价结果,需要将各项指标值化为一个取值范围相同的指数。即把不同量纲的指标变为无量纲数字。
为了评价的需要,对每个指标都进行分级操作,共分为5级,最优的为1级,次优的为2级,依此类推。对于需要定量评价的指标[11],在进行分级的过程中,应该建立指标值和对应指标的函数关系,这个函数关系是通过广义函数来实现的。广义函数法是在已知各单项指标权重和各项指标值的情况下,通过构造广义价值 (或效用) 函数,计算函数中各单项评价指标的指数 (价值),把指标值转化为得分,该函数为一连续分段函数。例如对于分级示例图 1,可以由式 (4) 进行计算,Z为对应指标的值。
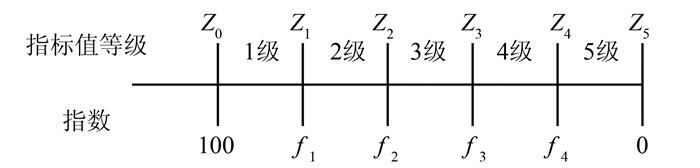 |
| 图 1 指标的分级示意 Figure 1 Classification of Indicators |
| $ \begin{array}{l} f = \\ \left\{ \begin{array}{l} {f_1} + \frac{{\left( {100- {f_1}} \right)\left( {Z- {Z_1}} \right)}}{{{Z_0}- {Z_1}}}, Z \in \left[{{Z_1}, {Z_0}} \right]或\left[{{Z_0}, {Z_1}} \right]\\ {f_2} + \frac{{\left( {{f_1} - {f_2}} \right)\left( {Z - {Z_2}} \right)}}{{{Z_1} - {Z_2}}}, {\rm{ }}Z \in \left[{{Z_2}, {Z_1}} \right]或[{Z_1}, {Z_2}]\\ {f_3} + \frac{{\left( {{f_2} - {f_3}} \right)\left( {Z - {Z_3}} \right)}}{{{Z_2} - {Z_3}}}, {\rm{ }}Z \in \left[{{Z_3}{Z_2}} \right]或[{Z_2}, {Z_3}]\\ {f_4} + \frac{{\left( {{f_3} - {f_4}} \right)\left( {Z - {Z_4}} \right)}}{{{Z_3} - {Z_4}}}, {\rm{ }}Z \in \left[{{Z_4}, {Z_3}} \right]或[{Z_3}, {Z_4}]\\ \frac{{{f_4} \times \left( {Z - {Z_5}} \right)}}{{{Z_4} - {Z_5}}}, {\rm{ }}Z \in \left[{{Z_5}, {Z_4}} \right]或[{Z_4}, {Z_5}] \end{array} \right. \end{array} $ | (4) |
本文尝试全面地阐述路径计算过程中可能遇到的阻力因子情况,希望能尽可能地反映出交通运输的真实情况。整个过程中做到科学、客观,最后建立阻力因子的评价指标体系。
本文列举的阻力因子有5类,分别是道路设施产生的阻力因子 (如机动车道数,路面间隔板的有无,路面材料,弯道弧度、弯道半径和弯道倾斜角,道路坡度,公交站点设施,行人过街设施,道路交叉口的设置,非机动车行驶专用车道的有无,接入口宽度,收费站或出入口)、气象因素产生的阻力因子 (如雾霾天气,雨雪、冰雹天气,沙尘天气)、时间变化产生的阻力因子 (如交通高峰,夜间时段)、交通规则产生的阻力因子 (如限速型法规,道路禁止转弯或禁止通行,禁行时段,路口信号配时) 和环境因素产生的阻力因子 (如土地利用类型,人口密度,警力部署)。另外,还有两种类型,分别是驾驶员本身和车辆产生的阻力因子,在这里都不考虑,因为在实际应用时驾驶员不会愿意提供自己的信息,而车辆情况的比较需要相关从业人员才能进行。
2.2 阻力因子体系建立在选取好阻力因子后,应该根据阻力因子的特点对阻力因子是否加入层次分析法进行判断。根据阻力因子是否强制性地影响道路的连通性进行分类,认为道路禁止转弯或禁止通行和禁行时段强制性地影响道路的连通性,不适合赋予权重。所以应该把这些阻力因子排除出层次分析法之外,并设计一套算法纳入这些因子。
另外,应该把与节点有关的阻力因子与有关道路的阻力因子分开,因为道路两端连接的是不同的节点,两个节点的阻力因子可能不同;一条道路的阻力会随着道路长度的增加而累积,而与节点有关的阻力因子不与道路的长度有关。最终与节点相关的阻力因子为道路交叉口的设置、路口信号配时和警力部署。
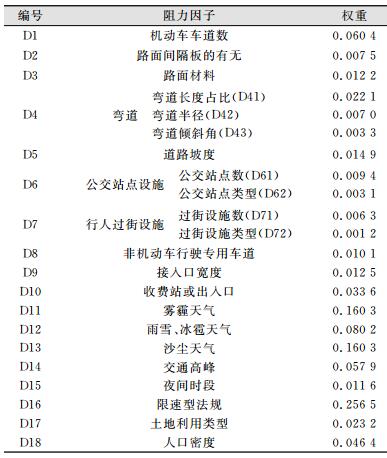
2.3 层次分析法获取阻力因子权重首先根据已经建立的层次结构模型,请多位专业人士评价因子的相对重要程度,根据专业人士评价的结果建立判断矩阵。建立好判断矩阵后,对矩阵进行计算,求得矩阵的CI和CR,用以判断矩阵的CR是否满足要求,如果满足要求,则求出矩阵的特征向量,最终得到道路和节点的阻力因子的权重,如表 3和表 4所示。
| 表 3 道路阻力因子权重 Table 3 Weight of Road Resistance Factors |
 |
| 表 4 节点阻力因子权重 Table 4 Weight of Junction Resistance Factors |
 |
2.4 阻力因子评价模型的建立
在确定权重之后,需要对决策中的每一个因子进行评判。在一个包含多项评价指标的体系中,各指标的量纲数值范围各不相同,为了得到一个恰当的综合评价结果,需要将各项指标值化为一个取值范围相同的指数。即把不同量纲的指标变为无量纲数字。本次评价系统选取的取值范围为[0, 100]。
确定决策中的指标的性质是定性还是定量以后,为了评价的需要,对每个指标都进行分级操作,共分为5级,最优的为1级,次优的为2级,依此类推。
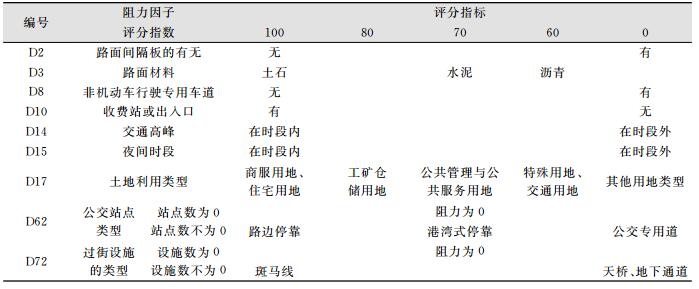
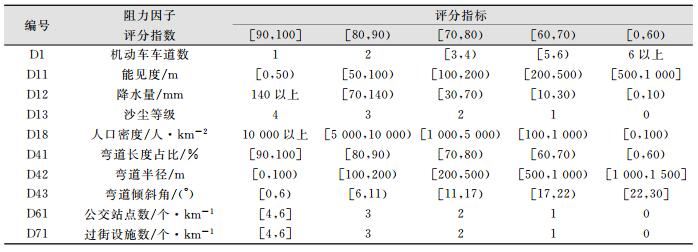
对于道路阻力因子,定性指标的分级如表 5所示,定量指标的分级如表 6所示,定性与定量相结合的指标分级如表 7所示。
| 表 5 道路阻力因子定性指标分级 Table 5 Qualitative Index Classification of Road Resistance Factors |
 |
| 表 6 道路阻力因子定量指标分级 Table 6 Quantitative Index Classification of Road Resistance Factors |
 |
| 表 7 道路阻力因子定性与定量相结合指标分级 Table 7 Combination of Qualitative and Quantitative Index Classification of Road Resistance Factors |
 |
得到指标评价方法以后,结合上一节已经确定的权重,就得到了非强制性的道路类型阻力因子的完整的模拟评价体系。评价后得到的是道路每km的阻力因子大小,所以评价后需要乘以道路的长度,得到道路的阻力因子总大小。
接着需要确定非强制性节点类型阻力因子的评价指标,它评价的是阻力因子的大小,其取值范围为[0, 5]。节点阻力因子的定性分级如表 8所示,定量分级如表 9所示。
| 表 8 节点阻力因子定性指标分级 Table 8 Qualitative Index Classification of Junction Resistance Factors |
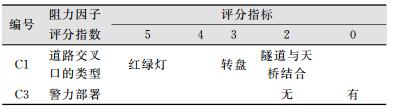 |
| 表 9 节点阻力因子定量指标分级 Table 9 Quantitative Index Classification of Junction Resistance Factors |
 |
综上所述,评价通过一条道路的总阻力因子,先要得到道路上的阻力因子乘以道路长度的值,还要分别得到道路两端节点的阻力因子的大小,最后把三者相加即可。
2.5 路径计算算法的设计完成评价模型的构建并且确定研究区域后,需要排除出层次分析法的阻力因子来决定道路的连通性,在Dijistra算法的基础上[12],设计合适的算法并编写程序完成计算。将建立的阻力因子评价模型应用于实例的流程如图 2所示。在这里,需要定义一个元组elementinmatrix (junction1, junction2, weight, edge, restrictID),其中,junction1和junction2表示道路两端的节点编号,weight表示从junction1到junction2方向的道路和它两端节点的总权重,edge表示道路的编号,restrictID表示从junction1到junction2方向无法通过的道路集合。
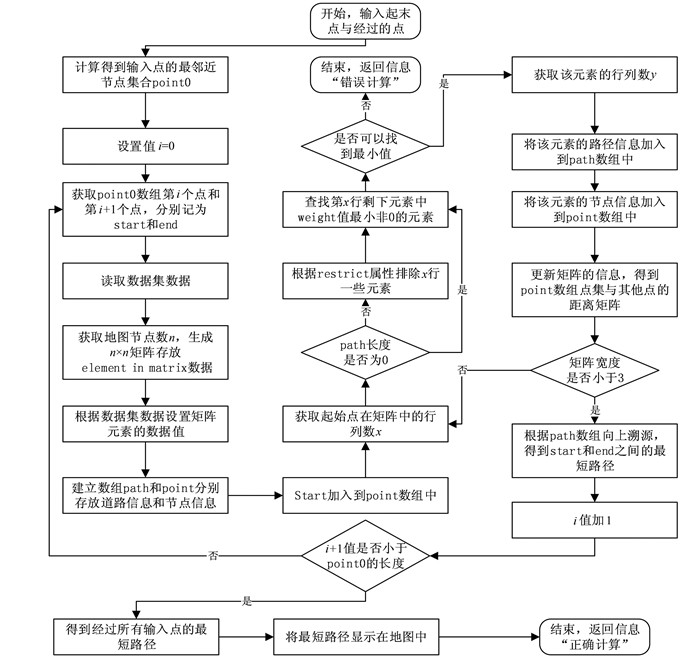 |
| 图 2 路径计算算法流程 Figure 2 Flow Chart of Path Calculation Algorithm |
3 阻力因子在实际路径计算中的应用
试验的基本流程为:① 构建整个程序的框架,需要设计地图显示的界面;② 选取有特点的区域以便进行分析;③ 导入数据,并根据道路禁止转弯或禁止通行和禁行时段等因子的值对道路的连通性和可达性进行判断;④ 根据评价模型对每一条道路和节点的权重进行计算,并将计算结果保存;⑤ 建立道路和节点的几何网络模型,并根据模型提取道路和节点的信息;⑥ 根据设计好的算法计算路径,求得最佳路径。
本次试验选择的道路数据为2006年的武汉市道路数据,选择C#语言搭建框架,最终搭建好的路径计算的平台如图 3所示。
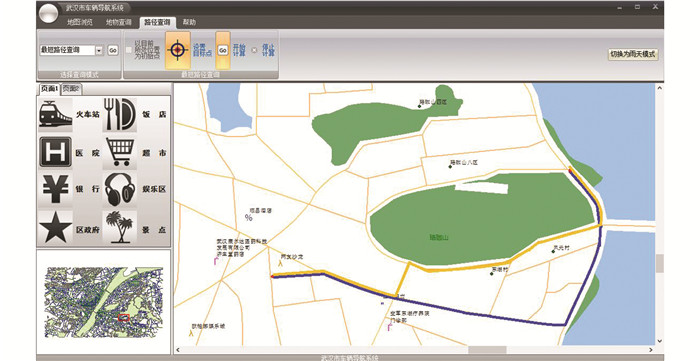 |
| 图 3 构建的程序框架图 Figure 3 Program Framework |
比较最短路径和考虑到阻力因子的最佳路径的区别。如图 4所示,黄色曲线是两个点之间的最短路径,蓝色曲线是两个点之间考虑到阻力因子的最佳路径。之所以有区别,是因为在考虑到阻力因子的计算时,出入口、车道数、坡度和限速对道路的阻力因子计算影响很大。蓝色曲线选取的道路大部分是主干道,道路的阻力因子比黄色曲线的道路阻力因子要小很多,计算得到的总的阻力因子要比黄色曲线小一些。
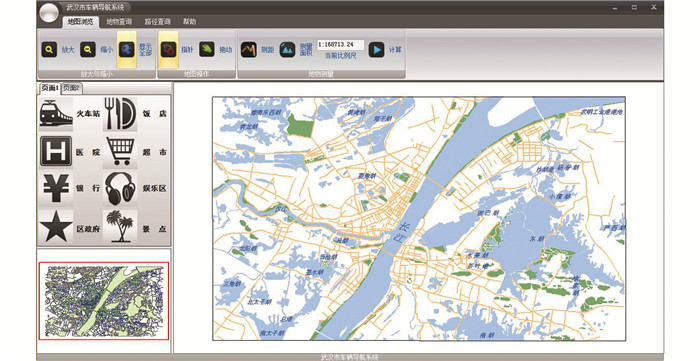 |
| 图 4 路径计算的对比 Figure 4 Comparison of Path Calculation |
选取多个起点与终点,计算考虑到阻力因子的最佳路径,并且根据得到的最佳路径结果进行实地驾驶调查或乘车调查,认为试验得到的最佳路径结果符合2006年实际交通情况的结果,既避开了阻力因子过大的路段,又考虑到一些道路的通行性限制,也确实是花费时间最短的路径结果。所以,建立好的阻力因子体系以及设计好的算法可以准确地应用于路径计算。一方面,阻力因子体系使得路径计算不再局限于道路长度,还加入了其他的因素,使得计算的结果更加精确可靠;另一方面,算法设计时也充分考虑了交通规则这种限制性、强制性的因素。
4 结束语本文对于路径计算中产生的各种阻力因子,利用层次分析法对各因子进行分析,并得到各自的权重;根据各个因子的特性对每个因子进行评判,建立了评价体系;针对一些特殊的阻力因子设计了一套路径计算算法。整个流程对路径计算中整合各种阻力因子有重要的借鉴意义。阻力因子评价模型的正确性基于两点,一是判断矩阵构造的精确性,二是对各个阻力因子指标评价的合理性。因此,要实现评价模型的广泛应用,首先在判断矩阵的构造方面,需要征集大量司机、专家等的意见;其次在因子的评判方面,需要广泛查阅文献,使得评判的标准更加科学;最后在算法的设计方面,解决了有向道路和道路可用性的问题,但是仍然不能应用于城市道路中日益兴起的立体交通,这也需要后续的研究。
| [1] | 谭惠丽, 黄乒花, 李华兵, 等. 交通灯控制下主干道的交通流研究[J]. 物理学报, 2003, 52(5): 1127–1131 DOI: 10.7498/aps.52.1127 |
| [2] | 徐进, 罗庆, 毛嘉川, 等. 考虑弯道几何要素和交通量影响的汽车行驶速度预测模型[J]. 中国公路学报, 2012, 25(5): 47–57 |
| [3] |
聂斌. 不同等级道路平曲线上的车速预测模型[C]. 全国城市公路学会第17届学术年会论文集, 绍兴, 2008 |
| [4] | 卢树, 陆化普, 唐忠华, 等. 城市道路行程车速影响因素分析[J]. 公路交通科技, 2003, (1): 89–92 |
| [5] | 伍剑奇, 符锌砂, 王晓飞. 基于平面线形运行速度预测模型研究[J]. 公路工程, 2009, (4): 89–93 |
| [6] | 陈铭, 王雪松. 城市主干路车速影响因素研究[J]. 交通与运输 (学术版), 2011, (2): 20–24 |
| [7] | 陈伟. 灾害天气下高速公路车速及间距控制研究[J]. 新西部旬刊, 2011, (9): 78–80 |
| [8] | 何杰. 雨天高速公路综合车速研究[J]. 科技创新导报, 2011, (6): 126–127 |
| [9] | 王晓原, 张敬磊, 邢丽. 基于人-车-路-环境综合计算的驾驶员期望车速[J]. 计算机工程与应用, 2012, (1): 223–227 |
| [10] | 杨辉. 基于差异性的路段交通内部稳定性评价研究[J]. 公路与汽运, 2013, (5): 65–67 |
| [11] |
贾珊珊. 基于多方法组合的城市交通指数评价研究[D]. 武汉: 武汉理工大学, 2008 |
| [12] | 黄邦菊, 林俊松, 郑潇雨, 等. 复杂地形下直升机救援最佳飞行路径分析[J]. 测绘地理信息, 2013, 38(5): 42–44 |
 2017, Vol. 42
2017, Vol. 42

