| 基于离群点探测准则和主成分分析的点云平面拟合效果研究 |
2. 山东省城市空间信息工程技术研究中心, 山东 济南,250013;
3. 济南市房产测绘研究院, 山东 济南,250001
2. Shandong Engineering Technology Research Center of Urban Spatial Information, Jinan 250013, China;
3. Jinan Real Estate Institute of Surveying and Mapping, Jinan 250001, China
三维激光扫描技术以其高效、精确获取扫描物体3D信息等优点得到广泛的应用,如古建筑物修复、隧道工程监测、建筑物整体形变监测等。蔡来良等[1]将三维激光扫描技术应用到建筑物形变监测,通过平面拟合获得建筑物整体形变信息,虽然扫描点云数据直接来源于物体表面,但是离群值,即边缘噪声对后续点云模型精度产生影响[2, 3],因此,点云预处理中需要探测出离群点并剔除。Papadimitrious等[4]提出将离群点探测方法分为3类:基于点云分布特征、基于二维深度统计和基于聚类方法。这3种方法的不足在于需要先验条件,并需要在不同实验条件下的点云进行探讨。
三维点云在采集过程中受到仪器、外界环境、物体遮挡等影响,获取的三维点云数据质量较差,尤其受到离群点的影响,对后续点云处理精度影响较大[5]。本文基于主成分分析方法能够获取复杂信息的主要特征的优势,对不同距离、分辨率等实验条件下的离群值进行探测并剔除,对剩余的三维点云进行平面拟合,能够较为稳定、准确地剔除噪声[6],提高了点云平面的拟合精度。
1 点云平面拟合方法和算法流程 1.1 离群值探测准则假设一维数据{pi(xi), i=1, …, n},对元素按升序排列,按式 (1) 得到该数据集的中位数:
| $\text{median}=\left\{ \begin{matrix} {{x}_{\left[ \left( n+1 \right)/2 \right]}},\text{当}n\text{为奇数} \\ \left[ {{x}_{\left( n/2 \right)}}+{{x}_{\left( n/2+1 \right)}} \right],\text{当}n\text{为偶数} \\ \end{matrix} \right.$ | (1) |
式中,median为数据集pi(xi) 的中位数;n为数据总数。根据式 (2) 计算出数据集的标准差:
| $s=\sqrt{\sum\limits_{i=1}^{n}{{{\left( {{x}_{i}}-\bar{x} \right)}^{2}}/\left( n-1 \right)}}$ | (2) |
式中,s表示数据集pi(xi) 的标准差;x=∑xi/n。由上述标准差和均值得到z-score标准化式:
| ${{z}_{i}}=\frac{\left| {{x}_{i}}-\bar{x} \right|}{s},i=1,\cdots ,n$ | (3) |
式中,zi为标准化后的数据。引入均值和标准差使得结果产生崩解值[7],即单个异常值可能引起均值和标准差与真实值偏差很大。因此,选择中位数和绝对中位数 (median absolute deviation, MAD) 代替均值和标准差。绝对中位数 (MAD) 为:
| $\text{MAD}=a\cdot \underset{i=1,\cdots ,n}{\mathop{\text{median}}}\,\left| {{x}_{i}}-\underset{j=1,\cdots ,n}{\mathop{\text{median}}}\,\left( {{x}_{j}} \right) \right|$ | (4) |
式中,a=1.482 6,该常量使得MAD在正态分布中具有无偏性;
| ${{R}_{{{z}_{k}}}}=\left( {{x}_{k}}-\underset{j=1,\cdots ,n}{\mathop{\text{median}}}\,\left( {{x}_{j}} \right) \right)/\text{MAD}$ | (5) |
式中,k=1, …, n。由此,得到离群点探测准则[6]:
| $\left\{ \begin{align} & \text{离群点},\text{当}{{R}_{{{z}_{k}}}}\ge 2.5 \\ & \text{局内点},\text{当}{{R}_{{{z}_{k}}}}<2.5 \\ \end{align} \right.$ | (6) |
主成分分析 (principal component analysis, PCA) 已经成为一个标准的数据分析工具:从神经科学到计算机图形分析等各个不同领域,该方法简单,利用无参数方法从复杂的数据集中提取出相关重要信息[8]。经过PCA降维能够提取出隐含在数据本质的内容。该方法通过主成分元素的变量反映数据的主次信息,通过对协方差特征分解得到观测值主成分及权值。第一主成分表示该方向分量对观测值的贡献率最大,具有最大权值,第二主成分次之,依次减少。
假设三维数据点集{Pi(xi, yi, zi), i=1, …, n},平面可定义为:
| $ax+by+cz+d=0$ | (7) |
式中,a、b、c是平面参数;d为各点到平面的距离。观测值的协方差矩阵定义为:
| $\mathit{\boldsymbol{E}}\left( x \right)=\frac{1}{k}\sum\limits_{i=1}^{k}{\left( {{p}_{i}}-\bar{p} \right)}{{\left( {{p}_{i}}-\bar{p} \right)}^{\rm{T}}}$ | (8) |
式中,
| $d = - \left( {a\bar x + b\bar y + c\bar z} \right)$ | (9) |
假设三维点云数据{Pi(xi, yi, zi), i=1, …, n},结合离群点探测准则和主成分分析平面拟合方法的具体算法流程如下:
1) 运用主成分分析方法拟合平面,得到平面参数a、b、c、d,计算点集Pi(xi, yi, zi) 中各点到拟合平面的距离xPi;
2) 对xPi利用式 (5) 计算z-score值Rzk,并根据准则 (6),当Rzk≥2.5被认定为离群值剔除,反之保留;
3) 对剩余的点集利用主成分分析方法进行平面拟合,求得平面参数 (a2, b2, c2, d2) 和各点到拟合平面的距离x2Pi;
4) 重复步骤2)、3),迭代直到由x'pi计算所得的Rzk均小于2.5为止,即所有点均被认为是局内点,然后利用主成分分析方法对局内点进行平面拟合。
2 实验及效果分析为验证算法的可行性,选择50 cm×30 cm的木板 (见图 1) 为扫描对象,扫描仪型号为Riegl VZ-400,扫描视角为100°×360°(竖直×水平),每秒扫描30万点。
 |
| 图 1 扫描物体及实验场 Figure 1 Scanning Objects and Experimental Field |
具体实验流程描述如下:
1) 架设扫描仪,对中整平并量取仪器高度,将木板分别架设在距离扫描仪10 m、20 m、30 m、40 m、50 m的三脚架上,木板高度与扫描仪高度一致,设置扫描分辨率为2 mm,扫描木板;
2) 为了探究不同扫描分辨率算法的适用性,选取20 m和50 m为扫描距离,分别设置分辨率为2 mm、5 mm和10 mm,扫描木板。
2.1 不同扫描距离实验结果及分析对不同距离实验采集的扫描点云利用§1.3的算法计算结果见表 1和图 2。
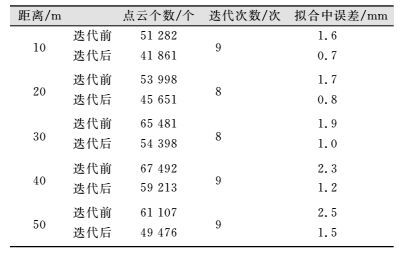
| 表 1 不同扫描距离拟合结果 Table 1 Fitting Results of Different Scanning Distances |
 |
 |
| 图 2 不同扫描距离拟合中误差及离群点比例 Figure 2 Fitting Error and the Proportion of Outliers of Different Scanning Distances |
从表 1和图 2看出,随着扫描距离的增加,点云拟合中误差增大,说明点云质量随着扫描距离的增加而降低;不同扫描距离迭代后拟合中误差明显小于迭代前;从迭代次数上看,不同扫描距离算法迭代次数最大相差1次,该算法较稳定。
将扫描木板点云及离群点剔除后点云效果显示见图 3,其中红色点表示离群点,绿色表示局内点,不同扫描距离的离群值去除较为明显,剔除效果较好。
 |
| 图 3 不同扫描距离点云剔除效果图 Figure 3 Eliminating Effect of Point Cloud of Different Scanning Distances |
2.2 不同扫描分辨率实验结果及分析
选择扫描距离为20 m和50 m,分别设置扫描分辨率2 mm、5 mm和10 mm,利用§1.3算法计算结果见表 2和图 4。
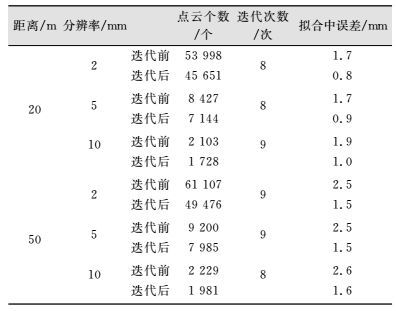
| 表 2 不同扫描分辨率拟合结果 Table 2 Fitting Results of Different Scanning Resolutions |
 |
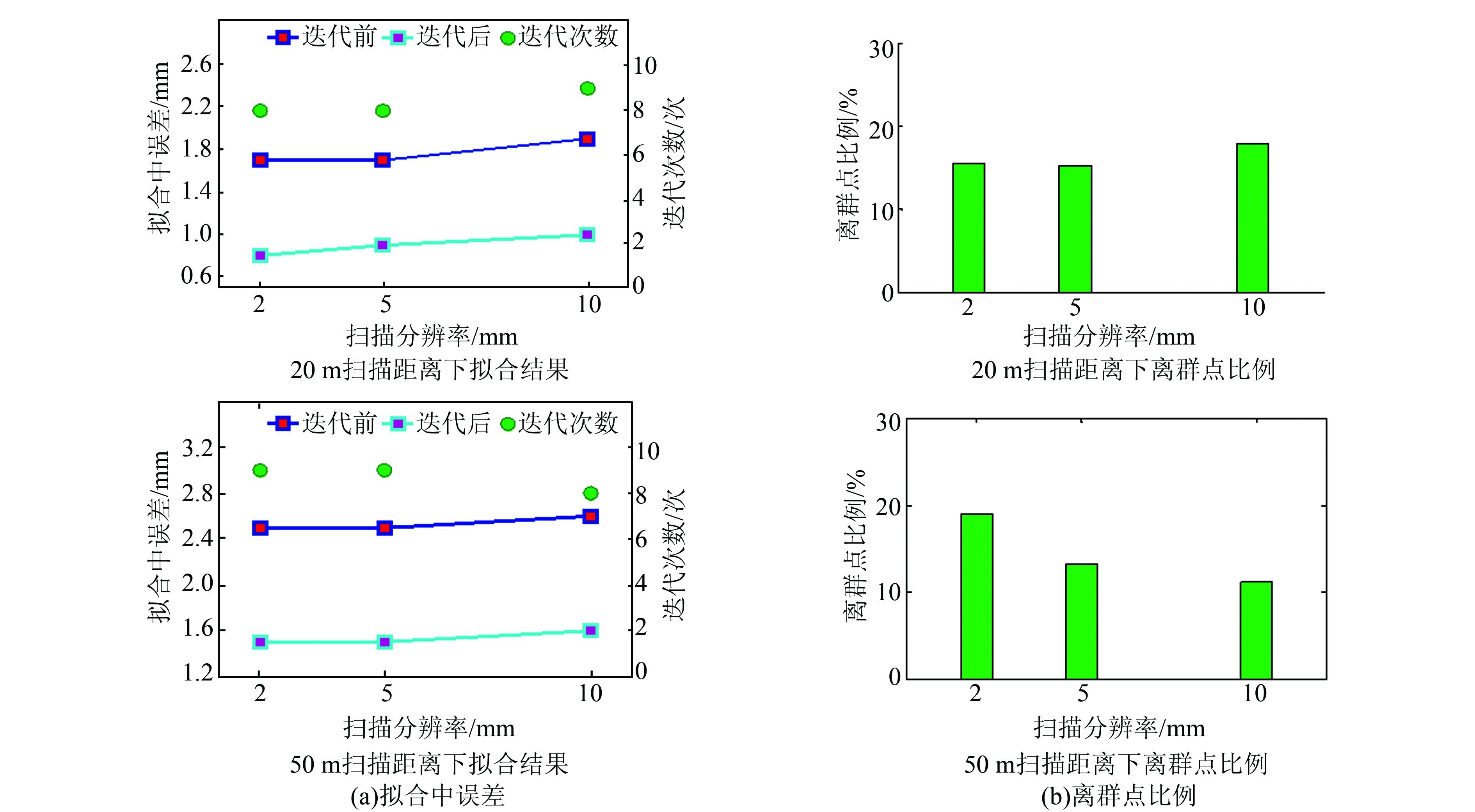 |
| 图 4 不同扫描分辨率拟合中误差及离群点比例 Figure 4 Fitting Error and the Proportion of Outliers of Different Scanning Resolutions |
从表 2看出,扫描距离为20 m和50 m时,拟合中误差随着扫描分辨率的增加而增大,说明点云质量随扫描分辨率的增加而降低;从迭代次数上看,20 m和50 m扫描距离下迭代次数最大差1次,该算法较为稳定。将不同分辨率下扫描木板点云及离群点剔除后点云效果显示见图 5,左侧3列表示20 m处不同分辨率点云,右侧3列表示50 m处不同分辨率点云其中红色点表示离群点,绿色表示局内点,可见剔除效果较好。
 |
| 图 5 不同扫描分辨率点云剔除效果 Figure 5 Eliminating Effect of Point Cloud of Different Scanning Resolutions |
3 结束语
本文以三维点云数据为研究对象,介绍了离群点探测的稳健法则,结合主成分分析方法,设计实验分析了不同扫描距离、不同扫描分辨率条件下该算法的适用性,实验结果表明:剔除离群值后的点云拟合平面精度较好,该三维点云离群点剔除方案效果较好,该算法能够在不同环境下较为准确的剔除噪声,提高了点云拟合的平面精度。
| [1] | 蔡来良, 吴侃, 张舒. 点云平面拟合在三维激光扫描仪变形监测中的应用[J]. 测绘科学, 2010, 9(5): 231–232 |
| [2] | Nurunnabi A, West G, Belton D. Outlier Detection and Robust Normal-curvature Estimation in Mobile Laser Scanning 3D Point Cloud Data[J]. Pattern Recognition, 2015, 48(4): 1404–1419 DOI: 10.1016/j.patcog.2014.10.014 |
| [3] | 李嘉, 林欢, 蓝秋萍, 等. 基于深度差的离群点识别与修正方法[J]. 测绘工程, 2014, 23(11): 1–6 DOI: 10.3969/j.issn.1006-7949.2014.11.001 |
| [4] | Papadimitrious S, Hiroyuki K, Gibbons P B, et al. LOCI: Fast Outlier Detection Using the Local Correlation Integral[C]. The 19th International Conference on Data Engineering, Bangalore, India, 2003 |
| [5] | 张树森, 伏利, 董刚. 离群点删除算法的研究[J]. 装备制造技术, 2008, (7): 13–15 |
| [6] | 崔希璋, 陶本藻, 王新洲, 等. 广义测量平差[M]. 武汉: 武汉大学出版社, 2009 |
| [7] | Rousseeuw P J, Hubert M. Robust Statistics for Outlier Detection[J]. Focus Article, 2011, (1): 73–79 |
| [8] | 浮丹丹, 周绍光, 徐洋, 等. 基于主成分分析的点云平面拟合技术研究[J]. 测绘工程, 2014, 23(4): 20–23 |
 2017, Vol. 42
2017, Vol. 42

