| 改进的Trim-ICP算法在面部整容中的应用 |
面部整容手术利用外科手术改善人的面部外貌和生理状况[1]。通过对比手术前后人脸的照片,可以感性地观察面部的改变情况,但无法准确地反映手术的改变程度和改变位置,也不能直观立体地展示手术前后的面部对比。利用三维扫描仪器对人脸的面部扫描可以得到三维数据,三维数据可以更完整准确地表现人的面部信息,可以给人以直观的立体感受。给定两片不同坐标系下或者相同坐标系不同位姿的具有一定重合度的点云,使用点云配准算法使其进行融合,使两片点云变换到相同的坐标系下并且融合为一个整体,在这个融合的整体上可以进行点云的变化检测和对比分析。
在众多点云配准算法中,经典的迭代最近点(iterative closest point, ICP)[2]配准算法是一种交替计算点对相关和求解运动参数由粗到精的配准算法,它具有思想简单和易于实现的特点,因此,广泛应用于点云配准。一些学者对该算法提出了改进,使用点到面之间距离测度代替了点到点的距离测度,改善了配准速度和精度,但是该算法中的法线评估容易受到采样密度和表面特征的复杂度的影响[3]。采用分配不同的点对权重替代相同的点对权重,改善含有噪声数据的点云的配准质量[4]。Trim-ICP采用部分相关点对参与运动参数的计算[5],增强了粗差点、丢失数据及初值的稳定性。一些学者把点云配准算法应用到变化检测上,根据地形数据的特点,在ICP的基础上,采用点到面的度量方式和修正权函数的稳健估计原则进行点云配准以及变化分析,得到了良好的断面检测效果[6]。采用ICP配准算法进行点云的配准,并在此基础上进行变化分析,能有效地进行点云的变化检测[7-9]。本文根据手术前后点云数据的特点,在Trim-ICP的基础上,引入了权重的方法,以达到改善配准和增强变化对比的效果,具体结合数据分析如下。
在手术前后人面部的三维数据采集的过程中,由于人面部和扫描仪相对位置的变化,不能保证采集到的两片点云具有良好的初始位姿,并且不同视角下的两片扫描点云间会存在没有对应关系的点,手术及表情变化也会产生面部表面模型的变化,假设手术后的扫描点集中每一个点都与手术前的扫描点集中的点根据最小距离测度构成点对,点云间构成的点对划分为以下3类:①1类点对不具有实体上对应关系的点对(外点)和受手术或表情影响较大的点对;②2类点对邻接手术部位或受表情影响形变较小的点对;③3类点对未经手术的部位中基本无改变的点对。
整体上这3类点对欧氏距离从大到小排序为:1类点对距离、2类点对距离、3类点对距离。考虑到1类点对距离相对比较大,利用Trim-ICP算法特点设置一定的重叠度排除这种干扰。2类点对、3类点对间的距离都相对较小,难以准确区分,如果使不同点对距离的点对权重相同,会使变化小的地方和变化较大的地方的优化程度折中,不利于使改变较小的地方得到更好的配准,使改变较大的地方得到更好的对比。本文在Trim-ICP的基础上,引入了权重的方法,使点对间距离越小的点对权重越大,点对间距离越大的点对权重越小,从而使改变越小的部位得到越好的配准,这样可以在准确配准的基础上改善对比效果。
1 配准方法设两片待进行配准的三维点云X、Y,X=(x1, x2, …, xN)为手术后的扫描点集,N为手术后的扫描点集的点个数;Y=(y1, y2, …, yM)为手术前的扫描点集,M为手术前扫描点集的点个数。
1.1 粗配准粗配准采用手动选点来选择相关点对, 用奇异值分解(singular value decomposition, SVD)的方法求解参数,流程如下:
1) 在手术后和手术前的点云上手动选择t对点(t≥3)。在手术后的点云上手动选择的点集为X′={x′1, x′2, …, x′t},在手术前的扫描点云上手动选择的对应的点集为Y′={y′1, y′2, …, y′t}。
2) 分别计算点集X′、Y′的重心为
3) 使用SVD分解得到参数旋转矩阵R和平移向量T:
| $ \mathit{\boldsymbol{A}} = \sum\limits_{i = 1}^t {({x_i}^\prime - } \hat x'){({y_i}^\prime - \hat y')^T} $ | (1) |
SVD分解为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{UD}}{\mathit{\boldsymbol{V}}^{\rm{T}}}\\ \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{UC}}{\mathit{\boldsymbol{V}}^{\rm{T}}}, \mathit{\boldsymbol{C}} = d\left( {1, \cdots , \det \left( {\mathit{\boldsymbol{U}}{\mathit{\boldsymbol{V}}^{\rm{T}}}} \right)} \right)\\ \mathit{\boldsymbol{T}} = \hat y' - \mathit{\boldsymbol{R}}\hat x' \end{array} \right. $ | (2) |
4) 更新手术后的面部扫描点集X中每个点xi为Rxi+T(i=1, …, N)。
1.2 改进的Trim-ICP算法假设手术后的扫描点集中每一个点都与手术前的扫描点集中的点根据最小距离测度构成点对,则总的点对个数为个N。设1类点对所占总点对比例为ξ,则参与配准的2类点对和3类点对个数,NC=N×(1-ξ)。把NC个点对根据点对距离进行加权,考虑到在初始位置时,点对间距离小的点对不一定是真实对应的点对,而此时距离稍大的点对获得一定的权重有助于朝着更稳健的方向配准,后期在重叠度稳定的情况下,使不同距离的点对对配准效果仍有差异性贡献率。本文使用的加权的规则如下:
| $ {w_i} = \frac{{2{d_{\max }} - {d_{{x_i}{y_i}}}}}{{2{d_{\max }}}} $ | (3) |
式中,yj为xi的最邻近点;dxiyi为xi、yj两点之间的欧氏距离;dmax为根据N个点对距离由小到大排序后的第NC个点对的距离。本文提出的方法针对这一种只在局部变形的点云数据具有良好的效果,可以自动对局部有变形的点云得到一个良好的重叠度,以及对变化区域能够得到更加真实的距离变化。
在数据点集中选择一个区域,区域的配准中误差(mean square error, MSE)表示为:
| $ {\rm{MS}}{{\rm{E}}_q} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{d_{{x_i}{y_i}}}} }}{n}} , {x_i} \in q $ | (4) |
式中,q表示数据点集中某个区域;n为该区域内的点个数。
Trim-ICP算法的流程如下:
1) 对于数据点云中的每个点xi, 在模型点集中查找最邻近点yj,点对间的距离表示为dxiyi。
2) 根据点对间的距离进行从小到大排序, 寻找优化重叠度,求得当前最优的ξ,选取前NC对点对参与配准。
3) 使用horn方法[10]求解旋转矩阵R以及平移向量T。
4) 更新手术后的面部扫描点集X中每个点xi为Rxi+T(i=1, …, N)。
5) 当满足最大迭代次数或者前后两次求解的旋转和平移参数的改变小于一定精度时或者中误差足够小时结束迭代,否则,转到步骤1)。
针对配准数据,本文对该算法的改进地方:①在步骤2)中加入按照式(3)进行前NC对点对权重计算;②在步骤3)中使用支持权重的horn方法求解旋转矩阵R以及平移向量T[11]。
2 试验及结果分析人面部有一定的弹性,当表情发生变化时,面部的局部形状就会发生变化,为获得良好的配准效果,需要手术人在手术前后尽可能保持相似的表情。实验数据为手术前后的点云数据,每个数据约60 000个点。初始设置1-ξ的搜索范围为[0.4,1.0]。图 1显示了在迭代配准过程中,重叠率的变化曲线。可以看到在经过15次迭代后,重叠率仅本上稳定在0.8左右。
 |
| 图 1 重叠度的计算 Fig.1 Calculation of Overlap Degree |
考虑到在手术前后扫描获得的点云的位姿并不一定接近,本文使用一组初始位姿差异较大的数据,进行了粗配准,然后分别进行了Trim-ICP配准和本文改进的Trim-ICP进行配准,为了描述算法带来的改善,在点云数据上选择了4个区域,进行区域中误差的比较,每个区域的中误差是根据式(5)得到。以图 2中(b)图中人面部为正方位,规定右眼右侧红色区域为区域1,嘴巴下侧黄色区域为区域2,左脸中部红色区域为区域3,鼻子右侧黄色区域为区域4,左眼上侧黄色区域为为区域5,区域1和区域3代表的是变形更小的区域,区域2和区域4和区域5代表变形更大的区域。实验得到的结果如图 3所示。
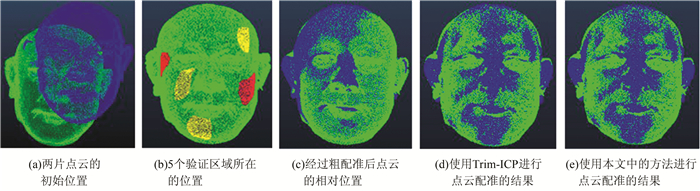 |
| 图 2 点云配准 Fig.2 Point Cloud Registration |
 |
| 图 3 配准结果的根据变形距离的分等定级显示图 Fig.3 Grading Image According to the Deformation Distance of the Registration Result |
图 4为5~30次迭代的5个区域距离中误差分布,各个子图中的蓝线表示的是在Trim-ICP下的区域中误差分布,红色的线表示为本文的方法的区域中误差的分布。
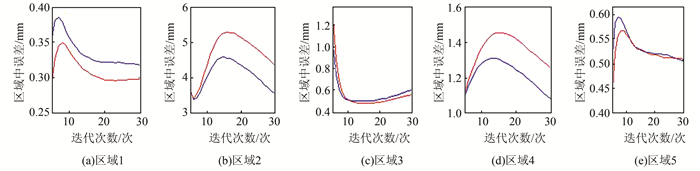 |
| 图 4 5个测试区域的点对距离误差分析 Fig.4 Point Pair's Distance Error Analysis of Five Test Area |
已经得知手术为隆鼻,消左腮、垫下巴和轻微的额头处理。由实验可知,根据图 2(d)和图 2(e)的配准情况可以看到,两种点云配准算法都可以很好地配准点云,得到正确的配准结果;根据图 3 (a)和图 3(b)中根据距离分级着色的显示来看,可以定量反映面部手术的改变情况;根据图 4中5个区域的中误差分布情况,图 4(e)表示该区域两种算法中误差基本相同;图 4(a)、图 4(c)表示本文的算法得到的区域中误差更小,说明可以使点对距离更小的区域得到更好的配准;图 4(b)、图 4(d)表示本文算法得到的区域中误差更大,说明点对距离较大的区域得到更好的对比,整体上达到了改变越小的地方配准越好,改变越大的地方对比越明显的效果。
3 结束语本文对整容前后面部点云数据间构成的相关点对类型进行了分析,采用改进的Trim-ICP算法配准手术前后的面部扫描点云。在保留了Trim-ICP算法对待粗差点,丢失点处理方法的基础上,针对具有部分形变的点云,提出了使用加权的方法,使变形越小的部分的点云配准越好,使变形较大的地方对比越明显。这样配准结果可以更好地准确反映手术前后人脸的变化情况,定量化手术的改变,给整容者以更直观的手术效果展示,也可以作为整容医生评价手术好坏的参考。
| [1] |
范金财. 整形美容外科的发展历史和展望[J]. 中国医药科学, 2011, 1(6): 5-6. |
| [2] |
Besl P J, Mckay N D. A Method for Registration of 3D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256. DOI:10.1109/34.121791 |
| [3] |
Chen Y, Medioni G. Object Modeling by Registration of Multiple Range Images[C].IEEE International Conference on Robotics and Automation, Sacramento, USA, 1991
|
| [4] |
Godin G, Rioux M, Baribeau R. Three-Dimensional Registration Using Range and Intensity Information[C]. Proceedings of SPIE: The International Society for Optical Engineering, Boston, 1994
|
| [5] |
Chetverikov D, Stepanov D, Krsek P. Robust Euclidean Alignment of 3D Point Sets: the Trimmed Iterative Closest Point Algorithm[J]. Image and Vision Computing, 2005, 23(3): 299-309. |
| [6] |
张良.基于多时相机载LiDAR数据的三维变化检测关键技术研究[D].武汉: 武汉大学, 2014
|
| [7] |
毕进超.三维激光扫描技术在危岩体变形监测中的应用研究[D].西安: 长安大学, 2015
|
| [8] |
刘绍堂, 刘文锴, 周跃寅. 一种隧道整体变形监测方法及其应用[J]. 武汉大学学报·信息科学版, 2014, 39(8): 981-986. |
| [9] |
姚艳丽, 蒋胜平, 王红平. 基于地面三维激光扫描仪的滑坡整体变形监测方法[J]. 测绘地理信息, 2014, 39(1): 50-53. |
| [10] |
Eggert D W, Lorusso A, Fisher R B. Estimating 3D Rigid Body Transformations: A Comparison of Four Major Algorithms[J]. Machine Visionand Applications, 1997, 9(5): 272-290. |
| [11] |
Tamaki T, Abe M, Raytchev B, et al. Softassign and EM-ICP on GPU[C]. International Conference on Networking and Computing, Higashi Hiroshima, Japan, 2010
|
 2018, Vol. 43
2018, Vol. 43

