| 超紧组合中不同精度IMU对GNSS信号跟踪性能的提升 |
现代战争的主流是越来越依赖高技术精确制导武器,低成本的导航与制导技术成为消耗型制导武器的关键技术之一。IMU/GNSS嵌入式组合导航系统具有重量轻、体积小、抗干扰能力强、动态性能高等优点,在军事应用等方面,精确制导武器具有十分重要的应用价值。本文研究了IMU / GNSS嵌入式组合导航系统的关键技术,分析了IMU辅助的GNSS信号跟踪环路误差,并对比分析了不同精度IMU对GNSS信号跟踪性能的影响。
1 接收机环路跟踪误差影响GNSS接收机跟踪性能的因素很多,一般根据跟踪环路误差大小确定GNSS接收机的信号跟踪能力。跟踪环路主要包括四种误差:动态应力误差、热噪声、艾伦方差相位噪声和由振动引起的相位噪声,如图 1所示。在接收信号与本地复制信号的相关过程中,主要是热噪声误差和动态应力起作用,而艾伦方差相位噪声和由振动引起的相位噪声主要对数字控制芯片产生的本振信号(numerically controlled oscillator,NCO)产生影响[1]。考虑到接收机的码延迟锁定环(delay locked loop,DLL)和载波锁相环(phase locked loop,PLL)的误差来源是相同的,PLL比DLL更敏感,更容易失锁,因此本文对超紧组合跟踪性能的分析和研究主要是针对锁相环。
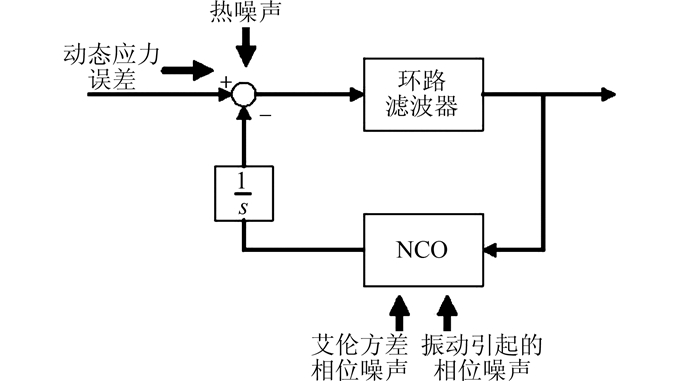 |
| 图 1 接收机跟踪环路误差 Figure 1 Receiver Errors in Tracking Loop |
1.1 动态应力误差
动态应力误差与接收机的运动有关,运动剧烈情况下,动态应力误差较大。动态应力误差在锁相环跟踪过程中不能避免,并起着主要作用,超紧组合技术正是用INS来估计接收机产生的动态运动,并对本地信号进行补偿,从而减少甚至消除动态应力误差,动态应力误差也与锁相环阶数有关,1σ的PLL动态应力误差为[2]:
| $\begin{align} & {{\theta }_{e}}=\frac{1}{3}\cdot \frac{{{d}^{k}}R/d{{t}^{k}}}{\omega _{\text{PLL}}^{k}}=\frac{1}{3}\cdot {{K}_{k}}\frac{{{d}^{k}}R/d{{t}^{k}}}{{{\left( {{B}_{\text{PLL}}} \right)}^{k}}}\left( m \right)= \\ & \frac{1}{3}\cdot {{K}_{k}}\frac{{{d}^{k}}R/d{{t}^{k}}}{{{\left( {{B}_{\text{PLL}}} \right)}^{k}}}\cdot \frac{360\cdot {{L}_{c}}}{c}\left( {}^\circ \right) \\ \end{align}$ | (1) |
式中,dkR/dtk是接收机与卫星在径向的相对运动;BPLL是PLL的环路噪声带宽;Lc是导航信号的载波频率;c是光速;Kk是与环路阶数有关的比例因子,二阶环时,k=2,K2=0.532=0.280 9;三阶环时,k=3,K3=0.784 53=0.482 8。
1.2 PLL的跟踪门限PLL跟踪阈值是指接收机确保PLL锁定时可以承受的最大相位误差,往往是通过多次实验决定的。然而,这个过程一般是复杂的,需要反复、大量的工作。测定跟踪阈值的保守的经验是不超过1/4锁相环鉴别器牵引范围的跟踪误差[2]。本文的研究就是根据这个标准确定跟踪阈值。由于跟踪相位误差包括热噪声、动态应力误差、艾伦方差相位噪声和由振动引起的相位噪声四个部分,所以确保PLL锁定的标准为:
| ${{\sigma }_{\text{PLL}}}={{\sigma }_{T}}+{{\theta }_{e}}+{{\theta }_{A}}+{{\theta }_{\varphi }}\le 15{}^\circ $ | (2) |
式中,σT是PLL的热噪声误差;θe是PLL的动态应力误差;θA是艾伦方差相位噪声误差;θφ是由振动引起的相位噪声误差;15°是1σ的PLL跟踪门限。
2 超紧组合环路跟踪误差在GNSS/INS组合导航系统中,动态和精确地利用IMU信息估计接收机动态,并补偿本地生成的导航信号,这样GNSS接收机的动态应力误差大大降低[3-6]。接收机经过动态补偿之后,剩余误差的动态应力主要是由加速度计测量误差引起的,所以在一个超紧组合导航系统中,锁相环的1σ动态应力误差可以表示为[1]:
| ${{\theta }_{\text{UT}}}=\frac{1}{3}\cdot {{K}_{k}}\cdot \frac{\delta a}{{{\left( {{B}_{\text{PLL}}} \right)}^{k}}}\cdot \frac{360\cdot {{L}_{c}}}{c}$ | (3) |
式中,δa是视线方向加速度计测量的载体加速度误差。
同时,通过加速度误差带来的IMU误差建模为[3]:
| $\delta {{f}_{\text{IMU}}}=\nabla +g\cdot a\left( 0 \right)+g\cdot \varepsilon \cdot {{t}_{d}}$ | (4) |
式中,∇是加速度计的零偏;ε是陀螺零偏;g是重力加速度矢量;α(0)是初始对准误差;td是漂移误差的时间。
假设通过IMU可以测量载体视线方向的加速度,则用δfIMU替换δa,得到超紧组合导航系统中PLL的动态应力误差:
| ${{\theta }_{\text{UT}}}=\frac{1}{3}\cdot {{K}_{k}}\cdot \frac{\delta {{f}_{\text{IMU}}}}{{{\left( {{B}_{\text{PLL}}} \right)}^{k}}}\cdot \frac{360\cdot {{L}_{c}}}{c}$ | (5) |
由此可见,超紧组合导航系统中PLL的动态应力误差主要取决于IMU误差。因此,IMU误差是超紧组合导航系统PLL误差中动态应力误差的主要决定误差项,由式(5)可以进一步写出超紧组合系统中锁相环的环路跟踪误差:
| ${{\sigma }_{\text{PLL}}}={{\sigma }_{T}}+{{\theta }_{\text{UT}}}+{{\theta }_{\text{A}}}+{{\theta }_{\varphi }}\le 15{}^\circ $ | (6) |
相位误差仍应小于15°的跟踪阈值,以确保锁相环能够正常保持跟踪。
由于载体的动态是通过IMU进行估计的,所以在超紧组合导航系统中IMU精度会对动态应力误差产生影响,从而进一步影响环路跟踪性能[7-10]。由上述公式可以得到超紧组合导航系统中PLL的动态应力误差与IMU误差的关系为:
| ${{\theta }_{\text{UT}}}=\frac{1}{3}\cdot {{K}_{k}}\cdot \frac{\nabla +g\cdot \alpha \left( 0 \right)+g\cdot \varepsilon \cdot {{t}_{d}}}{{{\left( {{B}_{\text{PLL}}} \right)}^{k}}}\cdot \frac{360\cdot {{L}_{c}}}{c}$ | (7) |
动态应力误差还与INS漂移所经历的时长有关,如果INS校准频率低,有很长一段时间的漂移,为了保证超紧组合导航系统的跟踪性能,要求IMU精度很高;若标定频率非常高,INS漂移时间短,则对IMU精度要求低,低精度的IMU也可以很好地保证超紧组合导航系统的跟踪性能。
3 IMU精度对跟踪性能的影响为了分析动态应力误差受IMU精度的影响,对采用4种不同精度IMU组成的不同超紧组合导航系统进行定量分析,4种不同精度IMU的陀螺零偏和加速度计零偏参数见表 1。
| 表 1 4种不同精度IMU的参数 Table 1 Parameters of Four Different Accuracy IMUs |
 |
假设超紧组合导航系统中惯导的校准频率为1 Hz,漂移时间为1 s,并且没有初始对准误差。以GPS的L1信号为例,设超紧组合最优环路噪声带宽为9 Hz,在载体加速度为10 g的动态条件下,表 2给出了不同精度IMU构成的超紧组合导航系统中二阶环路和三阶环路的动态应力误差。
| 表 2 IMU精度对不同环路阶数的动态应力误差/(°) Table 2 Dynamic Stress Errors of Different Stage by Different Grade IMUs/ (°) |
 |
从表 2可以看出, 在最优环路噪声带宽为9 Hz、载体加速度为10 g的动态条件下,无辅助的二阶PLL不能正常跟踪导航信号,无辅助三阶PLL动态应力误差也超过了15°,加上接收机热噪声等误差后也终将失锁。加入IMU辅助后,10 g的载体动态被IMU精确估计出来,使跟踪环路可以不受载体动态的影响,动态应力误差下降到10-2量级以下。随着IMU精度的提高,动态应力误差逐渐减小。在高动态条件下,不同精度的IMU对于二阶环路和三阶环路都可以精确辅助,从最终辅助效果的角度来说,低精度IMU和高精度IMU的区别不大。
假设超紧组合导航系统中INS的校正频率为1 Hz, 且无初始对准误差,以GPS的L1信号为例,图 2(a)、2(b)分别描绘了由不同精度IMU构成的超紧组合导航系统中,不同的环路噪声带宽对应的二阶环路和三阶环路的动态应力误差的变化情况。可以看出,在载体加速度为10 g的动态条件下,无辅助的二阶PLL不能在常用的15~25 Hz环路带宽范围正常跟踪,无辅助的三阶环路在25 Hz左右的环路带宽范围可以正常跟踪导航信号。加入IMU辅助后,可以显著降低环路带宽,使窄带宽跟踪环路成为可能,有利于提高接收机的抗干扰能力和测量值输出精度。随着IMU精度的提高,动态应力误差越来越小。对于MEMS IMU和民用级IMU等低精度的IMU,当超紧组合导航系统带宽较窄时,IMU误差会对锁相环跟踪动态应力误差和跟踪性能造成一定的影响;对于军事级IMU和导航级IMU等高精度的IMU,由IMU精度误差引起的动态应力误差远小于0.1°,因此可以忽略。
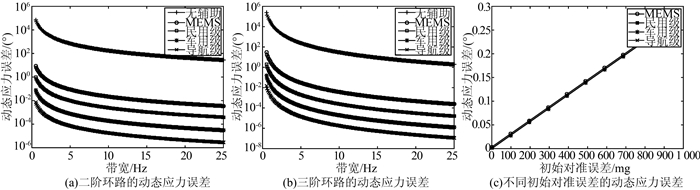 |
| 图 2 IMU精度对不同带宽和不同初始对准误差的动态应力误差 Figure 2 Dynamic Stress Errors of Different Bandwidth and Different Initial Alignment Errors Aided by Different Grade IMUs |
假设超紧组合导航系统中INS的校正频率为1 Hz,以GPS的L1信号为例,图 2(c)描绘了不同精度IMU构成的超紧组合导航系统中动态应力误差随初始对准误差的变化情况。
从图 2(c)可以看出, 随着IMU初始对准误差的增加,动态应力误差逐渐增大,且有近似于线性的比例关系。不同IMU精度所对应的动态应力误差线几乎重合,在1 000 mg的初始对准误差条件下,有近0.3°的动态应力误差。这一方面说明初始对准误差对所有精度的IMU来说具有近似相同的误差影响;另一方面,初始对准误差对环路跟踪的影响较小,降低了超紧组合导航系统对IMU初始对准精度的过度依赖,极大地方便了载体在运动过程中进行动态初始校准。
4 结束语本文建立了超紧组合导航系统跟踪环路误差数学模型,比较了常规卫星导航接收机和惯导辅助的超紧组合导航系统的跟踪环路误差和跟踪性能,对超紧组合导航系统进行了误差源分析,推导了系统总误差和IMU精度误差的关系,对超紧组合导航系统跟踪性能与IMU精度进行了定量分析。结果表明,IMU精度越高,跟踪性能越好,可以指数级提高二阶环路和三阶环路的动态跟踪能力,缩减环路跟踪带宽到窄带跟踪级别,且对IMU初始精度要求不高,有利于工程推广。
| [1] |
谢钢.
GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009 .
Xie Gang. Principles of GPS and Receiver Design[M]. Beijing: Publishing House of Electronics Industry, 2009 . |
| [2] | Kaplan E D, Hegarty C J. Understanding GPS: Principles and Applications[M]. Norwood: Artech House Inc, 2006 . |
| [3] |
秦永元.
惯性导航[M]. 北京: 科学出版社, 2006 .
Qin Yongyuan. Inertial Navigation[M]. Beijing: Publishing House of Science, 2006 . |
| [4] |
秦峰.基于矢量跟踪的高动态载体超紧耦合导航技术研究[D].上海:上海交通大学, 2014 Qin Feng. Research on Vector Tracking Based Ultra-Tightly Integrated Navigation for High Dynamic Vehicles[D]. Shangghai: Shangghai Jiao Tong University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10248-1015033364.htm |
| [5] |
苏玉瑞, 姬洪亮, 王晓南. GPS接收机内部噪声水平测试方法研究[J].
测绘地理信息,2014,37(12) : 118–119.
Su Yurui, Ji Hongliang, Wang Xiaonan. Research on the Test Method of GPS Receiver Interior Noise Level[J]. Journal of Geomatics,2014,37(12) : 118–119. |
| [6] |
郑凯, 郭斐. BDS/GPS单频软件接收机算法研究与实现[J].
测绘地理信息,2014,39(4) : 17–20.
Zheng Kai, Guo Fei. Research on BDS/GPS Single Frequency Software Receiver Algorithm[J]. Journal of Geomatics,2014,39(4) : 17–20. |
| [7] | Tsui J B Y. Fundamentals of Global Positioning System Reeeivers:A Software Approach[M]. New York: John Wiley & Sons Inc, 2000 . |
| [8] | Ziedan N I. GNSS Receiver for Weak Signals[M]. Boston, London: ARTECH House Publishers, 2006 . |
| [9] | Psiaki K L.Block Acquisition of Weak GPS Signals in a Software Receiver[C].ION GPS, Salt Lake City, UT, 2001 http://www.oalib.com/references/17410004 |
| [10] | Shin E. Estimation Techniques for Low-Cost InertialNavigation[D]. Calgary:The University of Calgary, 2005 |
 2016, Vol. 41
2016, Vol. 41

