| 日晷投影和等距离正圆柱投影在极区航海图编制及航海应用中的比较 |
2. 海军大连舰艇学院海洋测绘工程军队重点实验室,辽宁 大连,116018;
3. 91001 部队,北京,100161;
4. 海图信息中心,天津,300450
2. Key Laboratory of Hydrographic Surveying and Mapping of People's Liberation Army, Dalian Naval Academy, Dalian 116018, China;
3. Troops 91001, Beijing 100161, China;
4. Chart Information Center, Tianjin 300450, China
近年来,随着北极冰盖的消融速度加快,中国相关科技工作者为做好北极航道开通之前的航海保障准备工作,针对北极地区(简称极区)特殊的地理环境,从海洋调查、海洋测量、航海图书编制等方面开展了大量研究与实践,取得了不少富有价值的成果。李树军等[1]对编制极区航海图需解决的投影选择、制图资料收集与利用、专题符号设计和海图分幅4个关键问题进行了探讨,初步给出了相应的解决方案。王海波等[2]提出了一种适用于极区的横轴墨卡托航海图:为改变横轴墨卡托投影航海图上极区经纬线网格为三角形的特性和提高极区导航定位的精度,构建了基于伪经纬线网的横轴墨卡托航海图,使得图上的极区相当于墨卡托航海图上的赤道附近,伪经纬线网与墨卡托海图上经纬线网的特点相同。温朝江等[3]对墨卡托投影在极区航海图编制中的可用性进行了研究,从长度变形控制的角度,针对基准纬度的选用、最大长度变形的确定、图幅纬度的范围等影响因素,提出了提高墨卡托投影极区可用性的思路,重点讨论了适宜长度变形范围选用这一关键问题,按照基准纬度是否在图幅中纬的不同情况,分析了纬度75°~85°间墨卡托投影的可用性。随后,温朝江等[4]对可能用于极区航海图编制的双重极球面投影在极区的投影误差进行了分析,从投影变形、经纬线形状以及大圆航线与直线逼近程度等方面,探讨了极球面投影上用直线代替大圆航线的可行性。张志衡等[5]对极地航海区等距离正圆柱投影平面上等角航线的展绘方法进行了研究,从分析等角航线在等距离正圆柱投影中的方程及其曲率入手,得出等距离正圆柱投影面上等角航线一般为曲线的结论,在此基础上,应用“以直代曲”的研究思路,提出了一种在等距离正圆柱投影航海图上精确展绘等角航线的方法,并通过具体算例验证了该方法的可行性及实用性。随后,张志衡等[6]对等距离正圆柱投影在极区航海图中的应用问题进行了研究,提出了选用等距离正圆柱投影作为极区航海图投影的设想,并分析了该投影在极区航海图编制与应用中的适用性,研究了等角航线展绘和图上方位、距离量测等关键技术,为该投影在极区航海图中的应用提供了技术支撑。
虽然以上研究已经从不同角度探讨了包括投影选择和投影可用性等大量与极区航海图编制与应用有关的问题,但笔者认为,这些研究还未能全面解决极区航海图投影选择中需要解决的关键问题。为此,本文从给定投影在极区航海图编制和航海应用中的适用性角度,采取分析比较的方法,对编制极区航海图可能采用的日晷投影和等距离正圆柱投影进行了研究。
1 两种投影在极区航海图编制中的适用性比较分析 1.1 日晷投影 1.1.1 投影公式日晷投影是视点位于球心的透视投影,其投影公式如下[7, 8]:
| $ \left\{ {\begin{array}{*{20}{l}} {x = R\tan \theta \cos \lambda }\\ {y = - R\tan \theta \sin \lambda } \end{array}} \right. $ | (1) |
式中,R为视地球为球体时的半径;θ表示余纬度,θ = π/2 - φ,φ为球面纬度;λ为球面经度。
1.1.2 投影性质与特点1)球面上各垂直圈(所有通过切点的大圈)被描写为放射状的直线,各等高圈(垂直于垂直圈的平行圈)被描写为以切点为中心的同心圆。
2)两垂直圈之间的夹角与投影平面上相应的两直线间的夹角相等。
3)圆球上任何大圈都被描写成直线。
4)投影变形与其至切点的距离有关:切点附近变形小,距切点愈远变形愈大。即切点上长度比为1,随着其与切点间距离的增加,长度比不断增大,距切点90(°大圈距离)以上,长度比为无穷大。但在与切点为同一距离的等高圈上的长度比一致。
5)随着切点位置的不同,经纬线的形状也不同,有以下3种情况:
① 当切点在两极时,即为正方位投影,经线被描写为交于极点的放射状直线。放射中心各经线间的夹角与球面上的经差一致,同一纬线上的经差相等,纬线被描写成以极点为中心的同心圆,但各圆弧之间的距离并不相等,距切点愈远间隔愈大,至赤道为无穷大。
② 当切点在赤道上时,即为横方位投影,经线被描写成平行的直线,以通过切点的子午线(中央经线)为对称轴左右对称,平行线的间隔不等,离切点愈远间隔愈大,与切点经差为90°处的间隔为无穷大。赤道被描写成直线,其他纬线被描写为以赤道为对称轴的双曲线。离切点愈远,曲线间隔愈大,至两极为无穷大。
③ 当切点在极点和赤道以外的地球面上的任何一个位置时,即为斜方位投影,经线被描写为交于极点的一束放射状直线,各线间交角不相等。除赤道被描写为直线外,其他经线随位置的不同分别被描写为双曲线、抛物线或椭圆曲线(极点附近),曲线间的间隔随它与切点间的距离而变化,距切点愈远,间隔愈大。距切点大圈距离为90°处的变形为无穷大。
1.2 等距离正圆柱投影 1.2.1 投影公式等距离正圆柱投影是圆柱投影面与地轴平行,按经线长度不变的条件将经纬线网投影到圆柱面上,再沿某一母线剖开展平的一种投影。将地球视为半径为 R的球体时,可得到等距离正圆柱投影的一种常见形式——等距离正切圆柱投影,其投影公式如下[8]:
| $ \left\{ {\begin{array}{*{20}{l}} {x = R\varphi }\\ {y = R\lambda } \end{array}} \right. $ | (2) |
投影性质与特点如下[8]:
1)投影后的纬线间隔与实地等长,经线与纬线表现为相互垂直的等距平行直线。
2)视地球为球体时,经纬网为正方形格网,故等距离正圆柱投影又称为“方块投影”或“方格投影”。
3)从投影变形性质来看,等距离正圆柱投影属于任意投影,角度与面积均存在变形,长度只在经线方向与基准纬度处无变形,在其他区域与其他方向均存在变形。
1.3 两种投影的投影变形情况比较1)日晷投影的投影变形。如前文所述,日晷投影为任意投影,其变形公式如下[8]:
| $ \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {{\mu _1} = {{\sec }^2}\theta }\\ {{\mu _2} = \sec \theta } \end{array}}\\ {\begin{array}{*{20}{l}} {p = {{\sec }^3}\theta }\\ {\sin (\omega /2) = {{\tan }^2}\left( {\theta /2} \right)} \end{array}} \end{array}} \right. $ | (3) |
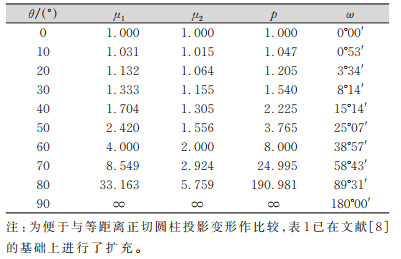
式中,μ1、μ2分别表示纬线圈和子午线方向上的长度变形,其中,μ1为日晷投影的极大长度变形,μ2为极小长度变形;p为面积变形;ω为角度变形。
表 1展示了若干典型余纬度θ处的日晷投影变形情况。
| 表 1 日晷投影变形信息 Tab.1 Deformation Information of Sundial Projection |
 |
2)等距离正圆柱投影的投影变形。与日晷投影一样,等距离正圆柱投影也是一种任意投影。当以赤道为基准纬度时即为等距离正切圆柱投影,而其纬线方向的长度变形、面积变形和角度变形将达到最大。为便于与日晷投影的投影变形作比较,以视地球为球体时的等距离正切圆柱投影为例进行分析,其变形公式为[8]:
| $ \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {m = 1}\\ {n = 1/\cos \varphi } \end{array}}\\ {\begin{array}{*{20}{l}} {p = 1/\cos \varphi }\\ {\sin \left( {\omega /2} \right) = {{\tan }^2}\left( {\varphi /2} \right)} \end{array}} \end{array}} \right. $ | (4) |
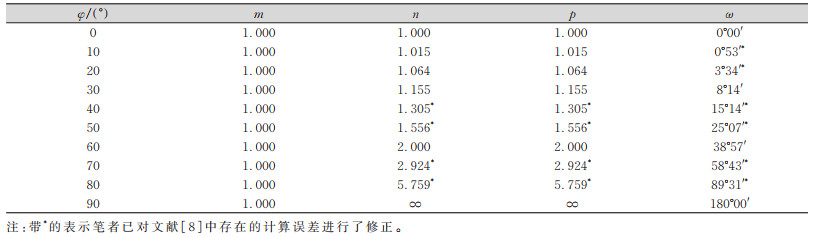
式中,m为经线方向长度比;n为纬线方向长度比;其余符号同前。表 2为若干典型球面纬度φ处的等距离正切圆柱投影变形情况。
| 表 2 等距离正切圆柱投影变形信息 Tab.2 Deformation Information of Equidistant Tangent Cylindrical Projection |
 |
1.4 两种投影极区航海图图幅设计难易比较
航海图图幅设计指的是按标准的航海图规格(图幅尺寸),根据比例尺、经纬线网和制图区域特点确定海图范围的过程。其中,图框计算是图幅设计中需要解决的关键技术问题,具体分为以下两种情况:①以经纬线为内图廓线时,准确求出4个图廓角点的经纬度值;②不将经纬线作为内图廓线时,大致确定出图幅范围。
两种投影极区航海图的图框计算方法如下:
1)日晷投影极区航海图的图框计算[9, 10]。由于日晷投影的经纬线不是成垂直正交的两组直线,因此,不能将经纬线作为内图廓线,这给采用该投影的极区航海图图框计算带来了困难,其主要过程如下:
① 确定图幅边缘的经纬度值。根据制图区域范围,确定出边缘的概略经纬度值。
② 计算并确定比例尺。计算边缘经线与北界纬线交点的纵坐标xN;计算边缘经线与南界纬线交点的横坐标y0;计算中央经线与南界纬线交点的纵坐标x0;根据计算得到的xN、y0和x0,计算横图廓和纵图廓的实地长度a'和b',其公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {a' = \left| {2{y_0}} \right|}\\ {b' = {x_N} - {y_0}} \end{array}} \right. $ | (5) |
假设航海图的规格为横向a0 cm、纵向b0 cm(即图幅尺寸或图积大小为a0 cm×b0 cm),则横向比例尺为a0/(a'× 100)、纵向比例尺为b0/(b'× 100)。在此基础上,取比例尺较小者并对比例尺分母进行必要的凑整,得到初步确定的比例尺分母C0。
③ 按初步确定的比例尺分母C0重新计算图积大小。分别将a'和b'乘以C0,将得到的新的a'、b'与a0、b0作比较。若相差较大,则通过调整制图区域的边缘纬度或改变比例尺分母C0的大小来调整制图区域的边缘经度。
④ 调整和试凑图幅范围。以规格图积为目标,通过切点不变、调整边缘纬度等方法反复进行调整和试凑,直至确定出符合规格图积的图幅范围。
尽管上述方法针对的是手工作业方式,但即使采用计算机制图技术,其过程也颇为复杂,往往要经过多次调整和人机交互处理,才能完成日晷投影极区航海图的图幅设计工作。
2)等距离正切圆柱投影极区航海图的图框计算。与日晷投影相比,由于等距离正切圆柱投影的经线与纬线表现为相互垂直的等距平行直线,这一性质使得其图幅设计工作变得十分简单,因为图幅的内图廓直接由上下两条纬线和东西两条经线构成。具体地,当地球半径为R、规格图积大小为a0 cm×b0 cm、比例尺分母为C0时,等距离正切圆柱投影极区航海图的图框计算过程如下:
① 计算图幅的横向经差和纵向纬差:
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta \lambda = {a_0}{C_0}/\left( {R \times 100} \right)}\\ {\Delta \varphi = {b_0}{C_0}/\left( {R \times 100} \right)} \end{array}} \right. $ | (6) |
式中,Δλ、Δφ分别表示横向经差和纵向纬差(单位:rad)。
② 通过给定图廓左下角点的经纬度φ南、λ西,得到图廓左上角点的经纬度为φ南 + Δφ、λ西,右上角点的经纬度为φ南 + Δφ、λ西 + Δλ,右下角点的经纬度为φ南、λ西 + Δλ。需要注意的是,具体作业时要将这些图廓点坐标转换为度分秒形式。
显然,若图幅覆盖的地理范围不合适,可首先将左下角点经纬度坐标φ南、λ西调整至理想位置,并在此基础上按前面的计算步骤得到所需的其余3个图廓角点的准确经纬度值。
2 两种投影在极区航海应用中的适用性比较分析 2.1 两种投影极区航海图上定位与量读难易比较在航海图上定位是应用海图的一种基本技术,有多种定位的方法,如距离法、方位距离法、三标两角法和经纬度值定位法等。同样地,在航海图上量读也是应用海图的一种基本技术,主要包括点位经纬度值量读、方位量读和距离量读等内容。本文以最常用也是最基础的经纬度值定位法和点位经纬度值量读为例,对两种投影极区航海图上的定位与量读难度进行比较[10]。
1)日晷投影极区航海图上定位与量读。本文以以极点为切点的正方位投影为例,介绍日晷投影极区航海图上确定点位的经纬度值定位法。如前文所述,由于该投影图上经线被描写为从极点出发的放射状直线,各经线的夹角与球面上的经差一致,且同一纬线上的经差相等;而纬线被描写成以极点为中心的同心圆,但各圆弧之间的距离并不相等,距切点愈远,间隔愈大,至赤道为无穷大。显然,在给定某点的经纬度值后,其困难在于准确定位该纬度值在图上的位置,即需要通过投影公式计算出该纬度值在图上的同心圆圆弧,而其经度值在图上的位置可根据其值的大小,在此同心圆圆弧上按照弧段距离等分法快速确定。
在日晷投影极区航海图上实现点位经纬度值量读,与上述经纬度值定位法原理是一致的,在此不再赘述。
显然,以人工的方法在日晷投影极区航海图上进行定位与量读并不是件容易的事情。事实上,在电子海图技术出现或得到实际应用之前,为解决相关问题,相关科技工作者曾通过编制出版《海图投影计算手册》[9]等工具书的途径,详细给出日晷投影图上各种实用的定位、量读与量测方法。
2)等距离正切圆柱投影极区航海图上定位与量读。与日晷投影极区航海图上确定点位的经纬度值定位法和实现点位经纬度值量读时的复杂性相比,由于球面等距离正切圆柱投影图上经纬线被投影为正方形格网,因此相应的方法都非常简单,均只需在经线和纬线上通过线段距离等分的方法即可快速、准确实现图上定位与量读。
2.2 两种投影极区航海图上等角航线与大圆航线绘制难易比较1)日晷投影极区航海图上等角航线与大圆航线绘制。由于日晷投影属于一种各种投影变形均比较大的任意投影,等角航线被描写成复杂的曲线,因此难以通过人工的方法在该投影图上绘制出等角航线。与此同时,从国内外已公开的文献中也无法查阅到如何利用计算机技术实现日晷投影图上等角航线绘制的方法。由此可见,还需要对如何在电子海图系统上实现该投影图上等角航线的自动绘制(显示)进行研究。但日晷投影上的大圆被投影成直线,因此,在该投影极区航海图上绘制大圆航线十分容易。
2)等距离正切圆柱投影极区航海图上等角航线与大圆航线绘制。通过表 1和表 2可以看出,与日晷投影相比,等距离正切圆柱投影是一种长度变形和面积变形都相对较小的任意投影,但相关文献表明,在该投影的航海图上等角航线与大圆航线均被描写成复杂的曲线,因此难以通过人工的方法绘制,而在电子海图系统上则可以按照“以直代曲”思路解决其自动绘制(显示)的问题[5, 6]。
2.3 两种投影极区航海图邻幅拼接难易比较日晷投影的性质和特点决定了其只适合用于制作单幅航海图,而不适合用于制作拼接使用的同一比例尺系列航海图。也就是说,若用这种投影制作极区航海图,要实现相邻图幅的拼接才能在航海时使用,存在明显的不便,这对依靠纸质航海图实施航海作业是十分不利的。
相比之下,等距离正切圆柱投影航海图上的经纬线网被描写为正方形,其经纬线网与墨卡托投影相似,甚至还因不存在纬度渐长而比墨卡托投影更简单,因此,非常容易实现任意方向相邻图幅的直接拼接使用。
3 结束语尽管在中国相关标准《中国航海图编绘规范》(GB 12320—1998)中对极区航海图投影已有明确规定,要求航海图制图区域60% 以上的地区纬度高于75°时,采用日晷投影,而不采用墨卡托投影。但相关研究已发现,简单地按照这一规定执行,在极区航海图编制和航海应用等关键环节中会存在不少需要解决的问题。为此,本文针对当前和今后可能应用于极区航海图编制与航海应用的日晷投影和等距离正圆柱投影,对其性质与特点、投影变形的大小与分布、图幅设计、图上定位与量读、图上等角航线与大圆航线绘制和邻幅拼接的难易等进行了分析与比较。从研究结果看,无论是在极区航海图编制还是航海应用中,与日晷投影相比,采用等距离正圆柱投影都具有更多的优势。因此,建议有关部门积极开展等距离正圆柱投影极区航海图编制实验,进一步解决其中可能存在的技术问题,扎实推进极区航海图正式生产的准备工作,更好地满足北极航线开通对极区航海图的迫切需要。
| [1] |
李树军, 张哲, 李惠雯, 等. 编制北极地区航海图有关问题的探讨[J]. 海洋测绘, 2012, 32(1): 58-60. DOI:10.3969/j.issn.1671-3044.2012.01.018 |
| [2] |
王海波, 张汉武, 张萍萍, 等. 一种适用于极区的横轴墨卡托海图[J]. 极地研究, 2017, 29(4): 454-460. |
| [3] |
温朝江, 卞鸿巍, 陈志红, 等. 墨卡托投影在极区航海图编制中的可用性研究[J]. 海洋测绘, 2014, 34(3): 56-59. DOI:10.3969/j.issn.1671-3044.2014.03.015 |
| [4] |
温朝江, 卞鸿巍, 陈秋, 等. 双重极球面投影的极区投影误差分析[J]. 海洋测绘, 2015, 35(1): 34-37. DOI:10.3969/j.issn.1671-3044.2015.01.009 |
| [5] |
张志衡, 彭认灿, 董箭, 等. 极地海区等距离正圆柱投影平面上等角航线的展绘方法[J]. 测绘科学技术学报, 2015, 32(5): 535-538. DOI:10.3969/j.issn.1673-6338.2015.05.020 |
| [6] |
张志衡, 彭认灿, 董箭, 等. 等距离正圆柱投影在极区海图中的应用研究[J]. 海洋测绘, 2018, 38(4): 67-70. DOI:10.3969/j.issn.1671-3044.2018.04.014 |
| [7] |
张晓平, 边少锋, 李忠美. 极区高斯投影与日晷投影的比较[J]. 武汉大学学报·信息科学版, 2015, 40(5): 667-672. |
| [8] |
李国藻, 杨启和, 胡定荃. 地图投影[M]. 北京: 解放军出版社, 1993.
|
| [9] |
《海图投影计算手册》编写组. 海图投影计算手册[M]. 天津: 海军司令部航海保证部, 1972.
|
| [10] |
楼锡淳, 朱鉴秋. 海图学概论[M]. 北京: 测绘出版社, 1993.
|
 2022, Vol. 47
2022, Vol. 47


