| 一种自适应伪距-相位比的精密单点定位随机模型方法 |
2. 中国地震局第一监测中心,天津,300180
2. First Crust Monitoring and Application Center, Tianjin 300180, China
精密单点定位(precise point positioning,PPP)技术使用非差的码伪距和载波相位观测值进行位置解算[1]。虽然使用伪距观测值不需要像相位观测值一样需要估算整周模糊度[2],但伪距的观测噪声远大于相位观测值[3],所以准确获得伪距和相位在PPP解算过程中所占的权比是随机过程的关键问题[4]。
传统的随机先验函数中伪距和相位比为一个常数,例如在确定精密单点定位随机模型的卫星高度角函数法或信噪比函数法当中,其先验函数中的常数项均取决于经验模型[5-11],在卫星高度角或信噪比强度较大时,直接通过固定伪距和相位观测值的方差比值实现随机模型的赋值。这个常数根据观测值噪声一般为码元长度的百分之一左右来确定,而伪距和相位的码元长度约为100:1,所以一般认为相位观测值较伪距观测值的精度高出2~3个数量级。目前,国际上一些知名的GPS数据精密处理软件普遍采用的伪距-相位噪声比值[12-15]为102~103。这种方法有其合理性且在实际应用中取得了很好的效果。
然而,实际测量中观测值的随机噪声不可能用一个固定的经验模型概括所有的情形。如果简单地将伪距观测值噪声固定为0.3 m或固定伪距-相位噪声比为100,这就势必会造成部分观测值精度虚高或虚低的假象,从而偏离观测值误差的真实分布。当伪距噪声较大,超过0.3 m甚至0.6 m时,采用固定观测值噪声方差0.3 m或固定伪距-相位噪声比100将会使过大的伪距噪声更多地引入精密单点定位结果中,这显然是不合理的。
本文针对这一缺陷提出了自适应伪距-相位噪声比方法。其关键在于数据处理过程中实时估计伪距噪声水平,将其作为随机模型的赋值依据。因为墨尔本-伍贝那(Melbourne-Wubbena,MW)组合观测值不仅消除了电离层延迟、对流层延迟,也消除了卫星钟差、接受机钟差和卫星至接收机之间的几何距离,仅受测量噪声和多路径误差的影响[16-20],所以本文利用MW组合观测值的离散程度来评估伪距噪声水平。当伪距噪声较大时,削弱伪距在精密单点定位中的作用,当伪距噪声较小时,提高伪距观测值在PPP初始化阶段的比例以缩短初始化时间。
1 基于自适应伪距-相位比随机模型解伪距和相位观测值噪声的随机特性是建立PPP观测值随机模型的前提。本文利用MW组合观测值进行噪声分析。
全球导航卫星系统(global navigation satellite system,GNSS)原始的伪距和载波相位观测方程为[20, 21]:
| $ \begin{array}{l} {P_{r, j}}^s = {\rho _r}^s + c({\rm{d}}{t_r} - {\rm{d}}{t^s}) + {T^s} + {I_{r, j}}^s + {e_{r, j}}^s\\ {\varphi _{r, j}}^s{\lambda _j} = {\rho _r}^s + c({\rm{d}}{t_r} - {\rm{d}}{t^s}) + {T^s} - {I_{r, j}}^s + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _j}{N_{r, j}}^s + {\varepsilon _{r, j}}^s \end{array} $ | (1) |
式中,r为接收机号;s为卫星号;下标j(j=1,2)为信号频率序号;为卫星至接收机之间真实几何距离,c是真空中光的传播速度;dtr和dts分别为r号接收机和s号卫星端的钟误差;Ts为斜路径对流层延迟;Ir, js为第j频率倾斜路径上的电离层延迟;Nr, js是相位观测值的整周模糊度;λj是第j频率载波波长;er, js表示伪距测量噪声;εr, js表示载波测量噪声;
基于式(1)中所列双频伪距和相位观测值逐历元逐卫星计算MW组合观测值[21]:
| $ MW = ({\varphi _1} - {\varphi _2}) - \frac{{{\rm{ }}{f_1}{P_1} + {f_2}{P_2}}}{{({f_1} + {f_2}) \times {\lambda _{WL}}}} = {N_{WL}} $ | (2) |
式中,P1、P2分别为相应频率上的P码观测值;φ1、φ2分别为相应频率上的载波相位观测值;f1、f2分别为P1、P2的频率;宽巷模糊度NWL=N2-N1,其中N1、N2为双频观测值整周模糊度;λWL为MW观测值即宽巷观测值的波长,计算公式为λWL=c/(f1-f2);当未发生周跳,且忽略相位观测值噪声影响时,N1、N2为常数,由此得到的MW组合观测值也将围绕某常数附近波动。
上述组合观测值不仅消除了电离层延迟,也消除了卫星钟差、接受机钟差和卫星至接收机之间的几何距离,仅受测量噪声和多路径误差的影响[21]。由于MW组合观测值包含整周模糊度,将受到周跳影响,首先需要利用有效的周跳和粗差探测方法剔除观测数据中的粗差并探测周跳,然后根据周跳信息将观测数据分成多个不同的观测弧段。在没有周跳和粗差的弧段内,MW观测值一般围绕某常数附近波动,这时采用滑动窗口法统计每个弧段内各历元MW组合观测值的标准差,以此来衡量伪距观测值的噪声水平。当然,前提是认为相位噪声和多路径效应足够小可以忽略不计。
首先对滑动窗口内MW观测值序列进行去均值化处理:
| $ {\rm{MW}}{\prime _i} = {\rm{MW}}{_i} - \left\langle {{\rm{MW}}} \right\rangle $ | (3) |
式中,<MW>为某一滑动窗口内所有MW观测值的平均值;MW′i和MWi分别为去均值后和去均值前历元时刻i的MW观测值。
引入衰减因子削弱与当前历元时间i间隔较长的历元信息对瞬时方差计算的贡献,计算历元i时刻的MW组合观测值的方差:
| $ D({\rm{MW}}{\prime _i}) = \sum\limits_{k = 0}^{n - 1} {{\beta _k}} {({\rm{MW}}{\prime _{i - k}})^2}/\sum\limits_{k = 0}^{n - 1} {{\beta _k}} $ | (4) |
式中,β(0 < β≤1)为衰减因子,采用以下方法计算:
| $ {\beta _k} = \frac{9}{{k + 9}}, 0 \le k \le n - 1 $ | (5) |
式中,n为该滑动窗口内的历元总数。需要说明的是,利用式(1)~式(3)计算得到的伪距噪声包含了多路径效应,而多路径效应具有一定的周期性。当连续弧段较长时,认为多路径效应造成的误差可忽略不计。本文根据经验设置滑动窗口长度为5~10 min,忽略多路径效应,又因为相位噪声远小于伪距噪声,忽略相位噪声对MW组合观测值的影响。
根据误差传播定律能够还原历元时刻i的伪距噪声标准差为:
| $ {\sigma _{{P_i}}} = \frac{{{\rm{ }}({f_1} + {f_2}) \times {\lambda _{WL}}}}{{\sqrt {{f_1}^2 + {f_2}^2} }} \times \sqrt {D({\rm{MW}}{\prime _i})} $ | (6) |
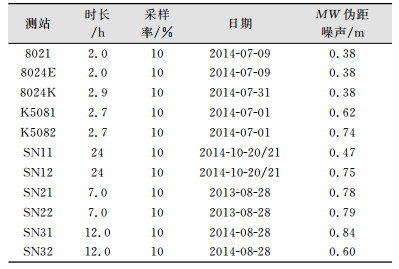
为了具体分析自适应伪距相位比方法的特点和定位性能,笔者分别进行了静态、模拟动态的精密单点定位试验。分别从定位精度、收敛性方面来对比分析固定比和自适应伪距相位比方法的定位性能。试验选取了10组10 s采样率的实测数据进行解算,这些实测数据采用司南接收机采集,观测位置位于上海市松山区佘山,观测信息如表 1所示。
| 表 1 实测数据信息 Tab.1 Information of Measured Data |
 |
为验证定位结果的正确性,以澳大利亚在线GPS软件AUSPOS精密网解结果所提供的测站坐标作为参考值,将解算结果与参考坐标做差,获得东(E)、北(N)、垂直(U)3个方向上的坐标偏差[22]。本文采用位置偏差均方差(root mean square, RMS)来表征定位精度[23]。为了分析两种PPP的定位收敛时间,使用单向滤波对上述10个测站分别进行静态、模拟动态PPP解算,并统计各测站定位偏差的水平分量优于0.1 m且垂直分量优于0.2 m时所需要的观测时长作为收敛时间指标。
3 基于自适应伪距-相位比实验结果分析采用国产接收机板卡的实测数据,其特点为普遍伪距噪声较大,且以上观测时长较短,所以本文得到的精密单点定位精度和收敛时间都较差,但这不影响本文对比分析固定比和自适应伪距相位比两种方法。
1) 精度分析。图 1和图 2给出了各测站PPP固定比与自适应伪距相位比结果精度比较。从图中可以看出,自适应伪距相位比的结果较固定伪距相位比为100的结果精度都有一定提高,伪距噪声越大,即伪距相位比越大时,精度提高越明显。例如K5081、K5082、SN21、SN22和SN32站,伪距噪声都超过0.6 m,而固定伪距相位比的缺省伪距噪声为0.3 m,所以在自适应方法中其伪距相位比升高了1倍以上,对应的测站定位精度提高非常明显,表 2代表性地给出了K5081、K5082两个测站精度和收敛速度提高水平。其余伪距噪声较小的测站,自适应伪距相位比与固定伪距相位比差距不是很明显,所以精度提高在图中不明显,但也有mm级的提高。统计结果显示,使用自适应伪距相位比的结果位置偏差均方差在E方向上平均提高23.4%,N方向上平均提高13.8%,U方向上平均提高17.7%。
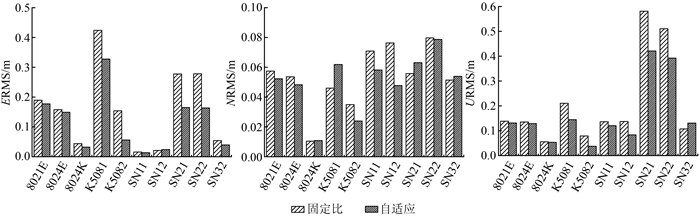 |
| 图 1 静态PPP固定比与自适应伪距相位比精度比较 Fig.1 Accuracy Comparison Under Fixed and Adaptive Pseudorange-Phase Ratio in Static PPP |
 |
| 图 2 动态PPP固定比与自适应伪距相位比精度比较 Fig.2 Accuracy Comparison Under Fixed and Adaptive Pseudorange-Phase Ratio in Kinematic PPP |
| 表 2 K5081和K5082站静态PPP精度和收敛速度提高水平/% Tab.2 The K5081 and K5082's improvement of accuracy and convergence time in static PPP/% |
 |
2) 收敛性分析。图 3代表性地给出了K5082站固定比与自适应伪距相位比静态PPP偏差序列,其中图 3(a)为实验结果中的固定比PPP偏差序列,图 3(b)为自适应伪距相位比偏差序列。图 4给出的则是SN22站动态PPP的偏差序列,上下图分别为固定比和自适应比的结果,图中画圈的部分显示在动态PPP模式下,由于该历元可用卫星数少于4个等原因导致PPP重新初始化过程,使用自适应伪距相位比的结果收敛时间有显著的缩短,而且使偏差序列更加平稳,精度更高。从两组序列对比中可以看出,采用自适应伪距相位比的结果在精密单点定位初始化阶段更大程度上提高了收敛速度,缩短了PPP初始化时间,使定位更快地达到相对稳定的程度。
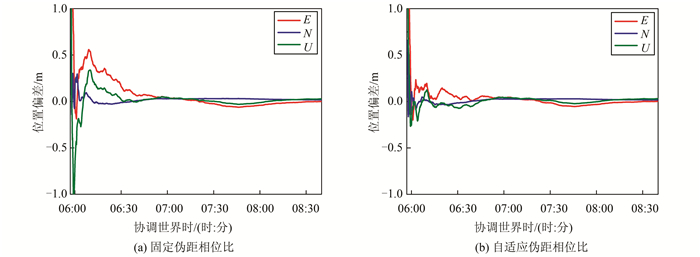 |
| 图 3 K5082站静态PPP固定比与自适应伪距相位比结果偏差序列比较 Fig.3 Static PPP Differences Sequence Comparison Under Fixed and Adaptive Pseudorange-Phase Ratio in K5082 Station |
 |
| 图 4 SN22站固定比与自适应伪距相位比偏差序列比较 Fig.4 Kinematic PPP Differences Sequence Comparison Under Fixed and Adaptive Pseudorange-Phase Ratio in SN22 Station |
图 5和图 6给出了10个测站的动态、静态收敛时间统计图。在图 6显示的结果当中,采用自适应伪距相位比的结果收敛速度提高明显,10个测站统计结果显示静态情况下的收敛时间平均缩短37.6%,动态情况下平均缩短34.6%。所以,当观测数据质量较差,尤其伪距噪声大于0.6m时,采用自适应伪距相位比的结果精度会有cm~dm级的提高,收敛速度会提高50%以上。
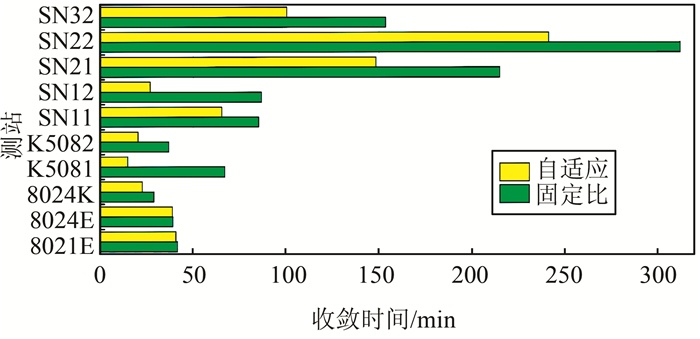 |
| 图 5 各站静态模拟动态PPP固定比与自适应伪距相位比收敛时间比较 Fig.5 Kinamtic PPP Convergence Time Comparison Under Fixed and Adaptive Pseudorange-Phase Ratio |
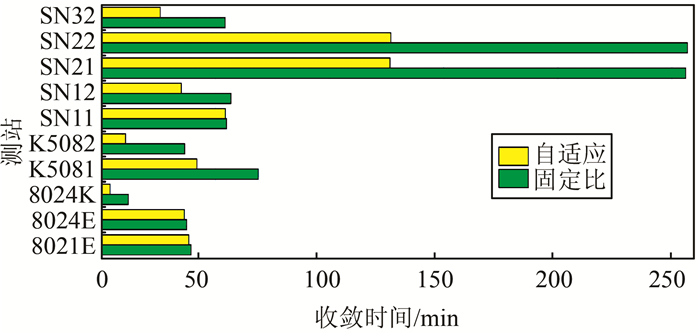 |
| 图 6 各站静态PPP固定比与自适应伪距相位比收敛时间比较 Fig.6 Static PPP Convergence Time Comparison Under Fixed and Adaptive Pseudorange-Phase Ratio |
4 结束语
本文针对传统的固定伪距相位噪声比存在的缺陷,即在伪距噪声较大或者较小时不适用的情况,提出了自适应的伪距相位噪声比方法。该方法基于MW组合观测值不仅能消除电离层延迟、对流层延迟,也能消除卫星钟差、接受机钟差和卫星至接收机之间的几何距离等误差,具有仅受模糊度、测量噪声和多路径误差影响的特性,根据MW组合观测值离散程度,采用滑动窗口和衰减记忆法实时估计伪距噪声,从而得到自适应的伪距-相位权比。自适应伪距-相位权比确定方法能有效提高定位精度和收敛时间,使用自适应伪距相位比的结果位置偏差均方差在E方向上平均提高23.4%,N方向上平均提高13.8%,U方向上平均提高17.7%;10个测站统计结果显示静态情况下的收敛时间平均缩短37.6%,动态情况下平均缩短34.6%。尤其是在观测值伪距噪声较大时,采用自适应伪距-相位权比的GNSS定位结果精度和收敛速度提高更明显。
| [1] |
Kouba J, Pierre Héroux. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28. DOI:10.1007/PL00012883 |
| [2] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [3] |
Hatch R R. The Synergism of GPS Code and Carrier Measurements[C]. International Geodetic Symposium on Satellite Doppler Positioning, USA, 1982
|
| [4] |
Bisnath S, Gao Y. Current State of Precise Point Positioning and Future Prospects and Limitations[C]. Observing our Changing Earth, IAG Symposia, Wuhan, 2009
|
| [5] |
Gao Y, Shen X. A New Method for Carrier-Phase-Based Precise Point Positioning[J]. Navigation, 2002, 49(2): 109-116. DOI:10.1002/j.2161-4296.2002.tb00260.x |
| [6] |
Seepersad G, Bisnath S. Reduction of PPP Convergence Period Through Pseudorange Multipath and Noise Mitigation[J]. GPS Solutions, 2015, 19(3): 369-379. DOI:10.1007/s10291-014-0395-3 |
| [7] |
Rui T, Ge M, Zhang H, et al. The Realization and Convergence Analysis of Combined PPP Based on Raw Observation[J]. Advances in Space Research, 2013, 52(1): 211-221. DOI:10.1016/j.asr.2013.03.005 |
| [8] |
Wu X L, Zhou J H, Wang G, et al. Multipath Error Detection and Correction for GEO/IGSO Satellites[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1297-1306. DOI:10.1007/s11433-012-4741-6 |
| [9] |
Dai W, Huang D, Cai C. Multipath Mitigation via Component Analysis Methods for GPS Dynamic Deformation Monitoring[J]. GPS Solutions, 2014, 18(3): 417-428. DOI:10.1007/s10291-013-0341-9 |
| [10] |
Tiberius C C J M, Kenselaar F. Estimation of the Stochastic Model for GPS Code and Phase Observables[J]. Empire Survey Review, 2000, 35(277): 441-454. DOI:10.1179/sre.2000.35.277.441 |
| [11] |
Cucurull L, Sedó P, Behrend D, et al. Integrating NWP Products into the Analysis of GPS Observables[J]. Physics & Chemistry of the Earth Parts A/B/C, 2002, 27(4/5): 377-383. |
| [12] |
Eueler H J, Goad C C. On Optimal Filtering of GPS Dual Frequency Observations Without Using Orbit Information[J]. Bulletin Géodésique, 1991, 65(2): 130-143. DOI:10.1007/BF00806368 |
| [13] |
Hartinger H, Brunner F K. Variances of GPS Phase Observations: The SIGMA-Model[J]. GPS Solutions, 1999, 2(4): 35-43. DOI:10.1007/PL00012765 |
| [14] |
Brunner F K, Hartinger H, Troyer L. GPS Signal Diffraction Modelling: The Stochastic SIGMA-Δ Model[J]. Journal of Geodesy, 1999, 73(5): 259-267. DOI:10.1007/s001900050242 |
| [15] |
Wieser A, Brunner F K. An Extended Weight Model for GPS Phase Observations[J]. Earth Planets and Space, 2000, 52(10): 777-782. DOI:10.1186/BF03352281 |
| [16] |
Dach R, Hugentobler U, Fridez P, et al. Bernese GPS Software Version 5.0, Astronomical Institute[R]. University of Bern, Switzerland, 2007
|
| [17] |
Teferle F N, Orliac E J, Bingley R M. An Assessment of Bernese GPS Software Precise Point Positioning Using IGS Final Products for Global Site Velocities[J]. GPS solutions, 2007, 11(3): 205-213. DOI:10.1007/s10291-006-0051-7 |
| [18] |
Herring T A, King R W, McClusky S C. Introduction to Gamit/Globk[R]. Mass Inst of Technol, Tech Rep, Cambridge, MA, 2008
|
| [19] |
Harris R B, Mach R G. The GPSTk: An Open Source GPS Toolkit[J]. GPS Solutions, 2007, 11(2): 145-150. DOI:10.1007/s10291-006-0043-7 |
| [20] |
Melbourne W G. The Case for Ranging in GPS-Based Geodetic Systems[C]. Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Boston, 1985
|
| [21] |
张守建, 李建成, 邹贤才, 等. GRACE卫星精密定轨随机模型精化[J]. 地球物理学报, 2010, 53(7): 1554-1561. DOI:10.3969/j.issn.0001-5733.2010.07.006 |
| [22] |
金鑫, 张景雄. 自适应加权中值滤波的InSAR干涉图去噪方法[J]. 测绘地理信息, 2016, 41(3): 12-15. |
| [23] |
韩菲, 张春燕. BERNESE5.0用于精密单点定位的数据处理及精度分析[J]. 测绘地理信息, 2015, 40(6): 28-31. |
 2019, Vol. 44
2019, Vol. 44

