| 原有测绘基准向CGCS2000统一的方法研究和实现 |
我国目前常用的坐标系有1954北京坐标系、1980西安坐标系和2000国家大地坐标系3种坐标系以及众多的地方独立坐标系[1]。由于历史原因,惠州存在市直部门之间和三县四区之间现有平面与高程系统不统一,测绘基准混乱,图件与数据无法拼接现象,各个地区甚至于同一地区的不同部门也可能存在不同坐标系下的测绘成果。不同测绘基准的采用造成测绘成果无法统一共享使用以及重复建设和浪费巨大,也给社会各应用部门带来许多不便,为后续工程测绘成果应用埋下了安全隐患,容易引发质量问题[2],客观上影响了全市经济社会建设和城市建设,逐渐发展成为限制惠州市数字城市建设下一步可持续发展的瓶颈问题。
为解决好这一难题,惠州市于2013-2014年间完成了全市范围内的B、C级GPS网的建设,并以此建立了惠州市现代测绘基准体系。按照广东省国土资源厅的统一要求,惠州市需要按条例规定保留一套全市统一的坐标系,废除其他坐标系,保证全市地理信息数据基准的一致性,建立一个能够为测绘成果数据进行高精度坐标转换的系统。在对原有控制成果进行分析的基础上,通过外业联测,利用公共点成果,确定现有各平面坐标系与1980西安坐标系及CGCS2000坐标系间高精度的转换参数,并搭建方便快捷的转换平台,实现了惠州市测绘基准的统一。
1 转换模型及精度评定原则 1.1 坐标转换模型 1.1.1 不同空间直角大地坐标系间的变换不同地球椭球基准下的空间直角大地坐标系统间的点位坐标转换的换算公式为布尔沙模型。涉及7个参数,即3个平移参数、3个旋转参数和1个尺度变化参数。公式为:
| $\begin{align} & \left[ \begin{matrix} {{X}_{N}} \\ {{Y}_{N}} \\ {{Z}_{N}} \\ \end{matrix} \right]=\left[ \begin{matrix} \Delta X \\ \Delta Y \\ \Delta Z \\ \end{matrix} \right]+ \\ & \left[ \begin{matrix} 0 & -Z & Y \\ Z & 0 & -X \\ -Y & X & 0 \\ \end{matrix} \right]\left[ \begin{matrix} {{\omega }_{x}} \\ {{\omega }_{y}} \\ {{\omega }_{z}} \\ \end{matrix} \right]+m\left[ \begin{matrix} X \\ Y \\ Z \\ \end{matrix} \right]+\left[ \begin{matrix} X \\ Y \\ Z \\ \end{matrix} \right] \\ \end{align}$ | (1) |
式中,
1) 三维七参数坐标转换模型。用于不同地球椭球基准下的大地坐标系统间的点位坐标转换,涉及3个平移参数、3个旋转参数和1个尺度变化参数,同时需顾及两种大地坐标系所对应的两个地球椭球长半轴和扁率差[4]。
2) 二维七参数转换模型。用于不同地球椭球基准下的椭球面上的点位坐标转换,涉及3个平移参数、3个旋转参数和1个尺度变化参数。公式为:
| $\left[ \begin{matrix} ~{{B}_{T}} \\ {{L}_{T}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{B}_{S}} \\ {{L}_{S}} \\ \end{matrix} \right]+\left[ \begin{matrix} \Delta B \\ \Delta L \\ \end{matrix} \right]$ | (2) |
式中,
| $\begin{align} & \left[ \begin{matrix} \Delta B \\ \Delta L \\ \end{matrix} \right]=\left[ \begin{matrix} -\frac{sin{{B}_{S}}cos{{L}_{S}}}{M} & -\frac{sin{{B}_{S}}sin{{L}_{S}}}{M} & \frac{cos{{B}_{S}}}{M} \\ -\frac{sin{{L}_{S}}}{Ncos{{B}_{S}}} & \frac{cos{{L}_{S}}}{Ncos{{B}_{S}}} & 0 \\ \end{matrix} \right]\cdot \\ & \left[ \begin{matrix} \Delta X \\ \Delta Y \\ \Delta Z \\ \end{matrix} \right]+\left[ \begin{matrix} -sin{{L}_{S}} & cos{{L}_{S}} & 0 \\ tan{{B}_{S}}cos{{L}_{S}} & tan{{B}_{S}}sin{{L}_{S}} & -1 \\ \end{matrix} \right]\left[ \begin{matrix} \varepsilon x \\ \varepsilon y \\ \varepsilon z \\ \end{matrix} \right]+ \\ & \left[ \begin{matrix} -\frac{N}{M}{{e}^{2}}sin{{B}_{S}}cos{{B}_{S}} \\ 0 \\ \end{matrix} \right]m+ \\ & \left[ \begin{matrix} {{\frac{N}{Ma}}_{S}}{{e}^{2}}sin{{B}_{S}}cos{{B}_{S}} & \frac{2-{{e}^{2}}si{{n}^{2}}{{B}_{S}}}{1-{{f}_{S}}} \\ 0 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} \Delta a \\ \Delta f \\ \end{matrix} \right] \\ \end{align}$ | (3) |
3) 三维四参数转换模型。用于局部坐标系间的坐标转换,涉及3个平移参数和1个旋转参数[6]。
4) 二维四参数转换模型。用于范围较小的不同高斯投影平面的坐标转换,涉及2个平移参数、1个旋转参数和1个尺度参数。对于三维坐标,需将坐标通过高斯投影变换得到平面坐标,再计算转换参数[7]。公式为:
| $\left[ \begin{matrix} {{x}_{T}} \\ ~{{y}_{T}} \\ \end{matrix} \right]=\left[ \begin{matrix} \Delta x \\ \Delta y \\ \end{matrix} \right]+\left( 1+m \right)\left[ \begin{matrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \\ \end{matrix} \right]\left[ \begin{matrix} {{x}_{S}} \\ {{y}_{S}} \\ \end{matrix} \right]$ | (4) |
式中,
5) 多项式拟合模型。用于全国、全省或相对独立的平面坐标系统的转换。公式同式(2)。其中,
| $\begin{align} & \Delta B或\Delta L={{a}_{1}}+{{a}_{2}}B+{{a}_{3}}L+{{a}_{4}}{{B}^{2}}+{{a}_{5}}BL+ \\ & {{a}_{6}}{{L}^{2}}+\ldots +{{a}_{20}}B{{L}^{4}}+{{a}_{21}}{{L}^{5}} \\ \end{align}$ | (5) |
式中,a1,a2,a3,…,a21为系数,可以通过最小二乘求解。
1.2 坐标转换精度估计1) 重合点残差
V=重合点转换坐标值-重合点已知坐标值
2) 点位中误差
| ${{M}_{p}}=\pm \sqrt{M_{X}^{2}+M_{Y}^{2}+M_{Z}^{2}}$ | (6) |
式中,空间直角坐标X、Y、Z的残差中误差分别为
3) 平面点位中误差
| ${{M}_{p}}=\pm \sqrt{M_{x}^{2}+M_{y}^{2}}$ | (7) |
式中,平面坐标x、y的残差中误差分别为Mx=$\pm \sqrt{\frac{{{\left[ vv \right]}_{X}}}{n-1}},{{M}_{y}}=\pm \sqrt{\frac{{{\left[ vv \right]}_{Y}}}{n-1}}$;n为点位个数[9]。
1.3 转换参数确定为了判断上述各种坐标转换模型的使用条件,选择合适的坐标转换模型,以惠州市1980坐标系与2000国家大地坐标系之间的坐标转换为例,在新布设的215个控制点中,选择了计算点205个,检核点10个,分别采用上述模型进行坐标转换,并对坐标转换结果及精度进行比较分析。
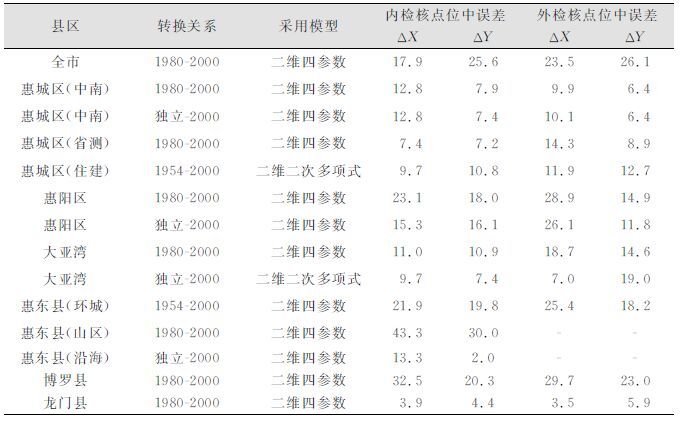
通过上述计算和比较分析可知,采用二维整体法精度最高,二维四参数精度最低。但是采用二维四参数外检核点位中误差小于4 cm,满足转换精度要求。考虑到二维整体法有参数,具备此转换模型的软件较少,为提高转换参数的可移植性,最终主要采用二维四参数,在二维四参数不满足精度要求下优先选用二维多项式。各县区转换精度如表 1所示。
2 软件实现 2.1 软件主体功能本项目前期调研过程中,收集了现有地理信息相关数据格式和各部门对转换软件的需要,针对需求,基于C语言编制了惠州市现代测绘基准服务平台。此平台是针对惠州市各地区的高精度坐标转换系统,系统能适应惠州市各单位现有的测绘成果文件格式,在规范下完成坐标转换,并且在保证坐标精度的条件下,简化系统操作界面,使系统软件使用方法更加人性化,使用户能更加简便地得到理想的转换成果,增加系统的可用性与实用性。
| 表 1 各县区转换精度统计/mm Table 1 Statistical Precision for Tranformation/mm |
 |
本系统功能分为权限管理、控制点查询、转换模块设计、单点转换、矢栅转换、高程转换等功能,系统主要功能如图 1所示。
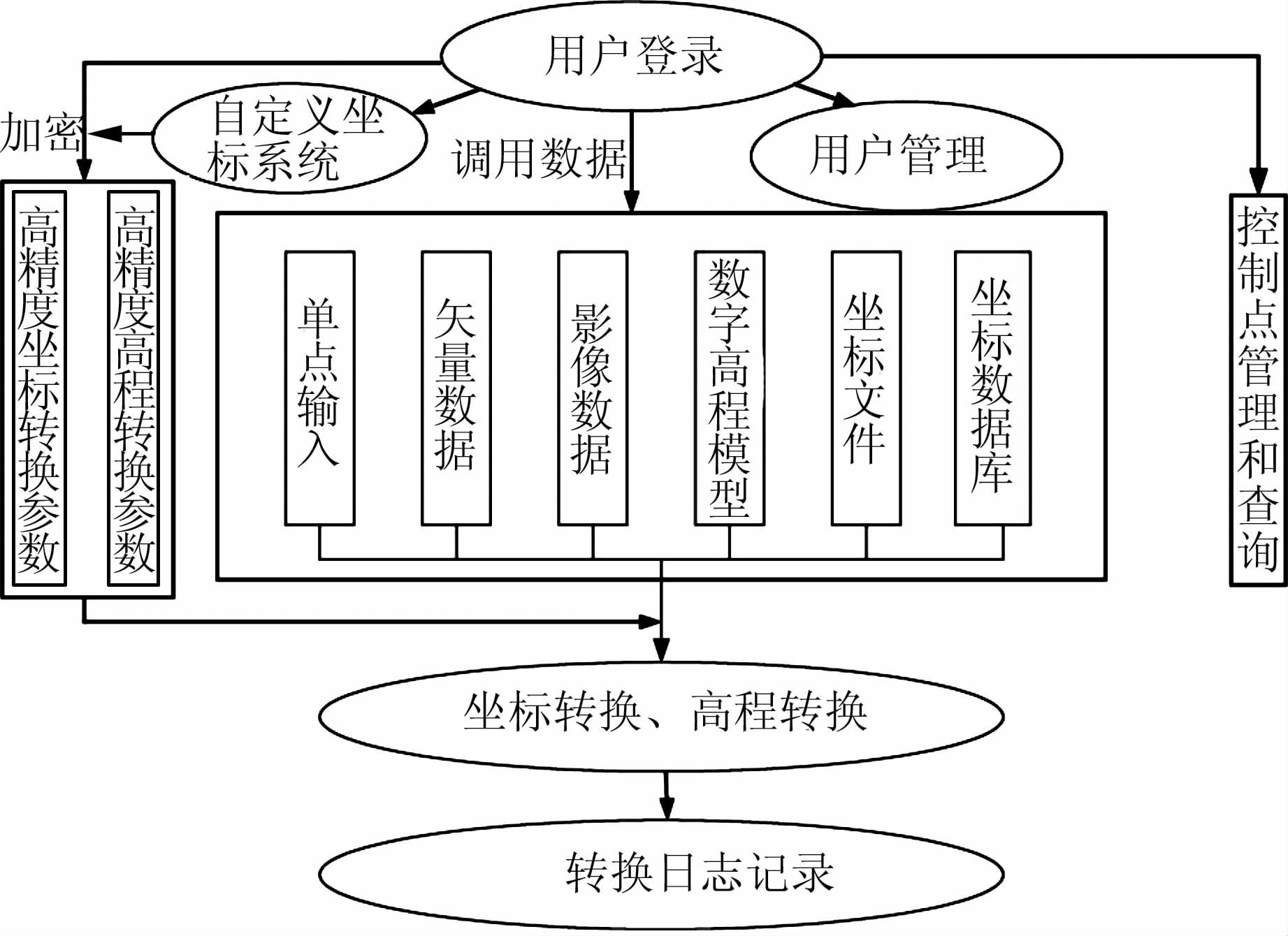 |
| 图 1 软件实现模块图 Figure 1 Graph of Software Realization |
平台采用SQLserver数据库管理现有的全部转换参数,以加密乱码形式存储。通过权限管理模块,管理和分配系统登录权限,包括可查看转换模型关系、自定义坐标系等功能的管理员和只能调用现有参数的普通用户,保证转换参数的保密性。
控制点管理和转换模块设计两部分,支持用户对现有的控制成果进行管理,并自选公共点坐标求取所需的转换参数,自动存储在平台内,方便后期调用。
单点转换、矢栅转换等坐标转换模块支持现有的主流形式数据使用参数模板转换和同椭球基准投影换带计算两个功能。操作流程只需选定原始数据和转换数据路径,勾选所对应的转换参数即可完成转换。操作过程简便、清晰。
2.2 外业工作开展外业工作开展的关键点在于对原有控制成果的收集和转换公共点的选取。在项目开始初期,多次对惠州市3县4区的国土、规划等部门进行调研,收集现有控制网成果,包括点位图、联测图、原始观测数据和最终成果等。收集的资料情况如表 2所示。
| 表 2 惠州市各县区坐标系统计表 Table 2 Statistical Coordinate Systems in Huizhou |
 |
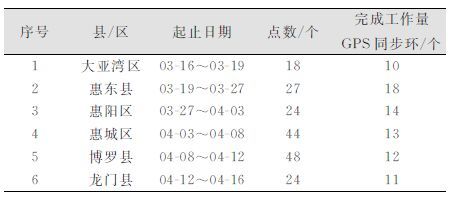
从表 2可知,惠州市国土系统主要采用1980西安坐标系,规划部门主要采用1954北京坐标系,由于原有控制网都是分批建设,因此所有原有控制网都要分别建立转换关系。根据提供的现有平面控制点的分布情况,均匀选择合适数量的控制点与惠州市新建的控制网(B/C级GPS网)联测,由于原有控制网多为E级GPS网,故平面联测采用D级GPS网要求施测。外业联测点数和环数如表 3所示。
| 表 3 外业联测工作量统计 Table 3 Statistical Works for Surveying |
 |
2.3 外业成果解算
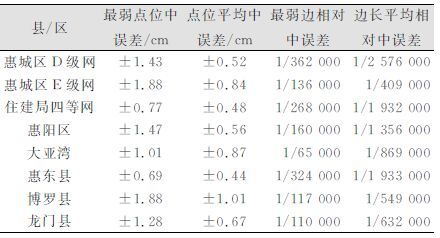
利用外业观测基线,解算得到各联测点的全市统一CGCS2000成果。整体平差采用科傻GPS数据处理软件。对于有原始观测数据的,以联测点的新成果为起算,重新整网平差得到全网CGCS2000成果,既保证了所有控制点CGCS2000成果的高精度,也为转换关系求取提供更多的公共点选择;对于没有原始观测数据的,则利用联测点作为公共点计算转换参数,实现原有控制成果向CGCS2000的转换。最终解算精度情况如表 4所示。
| 表 4 二维平差结果统计表 Table 4 Statistical Results for 2D Adjustment |
 |
2.4 软件应用效果
平台开发完成后,对现有数据进行转换,运行数据为惠州市市本级基础数据,数据大小约1 T,数据格式包括dwg、shp、gdb、tif、asc、adf等格式。
由于原有各比例尺数据线画图数据量较大,需要先整理再转换,整个工作持续了约一个月时间。通过具体工作中的问题进一步完善了软件,保证系统功能完全符合系统详细设计说明书中的要求,能在惠州市各单位现有测绘成果文件格式与规范下完成坐标转换,并且能够保证转换后图形要素及属性完整,系统总体上满足惠州市统一测绘基准的要求,系统运行日趋稳定,系统操作界面设计简单、人性化,系统可用性与实用性强。
3 结束语惠州市统一测绘基准工作的重点是转换参数的精度和转换平台的无损高效。通过多次的调研、收集资料,保证了对各县区现有控制成果的充分收集,针对不同的控制网进行高精度的外业联测,保证了转换参数的全覆盖和高精度。通过构建综合服务平台,实现了主流数据格式的统一转换。随着统一测绘基准工作的进一步推进,相信惠州市能在较短的时间内解决原来坐标系统不统一所带来的问题,实现真正全面应用2000国家大地坐标系,从而有利于城市建设和开发纳入一个统一的地理空间定位管理体系,实现测绘图件与地理信息数据在全市范围的无缝拼接,方便政府决策和各部门工作的开展,避免无序的管理、定位矛盾和工程隐患[10];有利于为大型基础设施建设、权属测量等各项工作提供强有力的测绘保障;有利于数字城市建设地理空间信息资源共享,减少重复测绘和资源浪费,提高城市建设的管理水平。
| [1] |
程鹏飞, 成英燕, 文汉江, 等.
2000国家大地坐标系实用宝典. 北京: 测绘出版社[M]. 2008 .
Chen Pengfei, Cheng Yingyan, Wen Hanjiang, et al. Practical Manual on CGCS2000. Beijing: Surveying and Mapping Press[M]. 2008 . |
| [2] |
李东, 毛之琳. 地方坐标系向2000国家大地坐标系转换方法的研究[J].
测绘与空间地理信息,2010,33(6) : 193–196.
Li Dong, Mao Zhilin. Research on Tranformation Methods from Local Coordinate System into CGCS 2000[J]. Geomatics & Spatial Information Technology,2010,33(6) : 193–196. |
| [3] |
孟庆武, 张洪文, 朱李忠. 基于CGCS2000的高斯平面坐标与城市独立平面坐标转换的研究[J].
测绘与空间地理信息,2012,35(11) : 160–164.
Meng Qingwu, Zhang Hongwen, Zhu Lizhong. A Study of the Conversion Between Gauss Plane Coordinate and Urban Independent Plane Coordinate[J]. Geomatics & Spatial Information Technology,2012,35(11) : 160–164. |
| [4] |
孟泱, 戴明松, 冯发杰, 等. CGCS2000坐标系对现有测绘成果的影响及坐标转换方法的探讨[J].
工程勘察,2010,(S1) : 683–687.
Meng Yang, Dai Mingsong, Feng Fajie, et al. Influence of CGCS2000 to Existing Surveying and Mapping Productions and Coordinate Transformation Methods[J]. Geotechnical Investigation & Surveying,2010,(S1) : 683–687. |
| [5] |
焦立芬. 基于坐标转换重合点的分布、密度、精度与转换精度分析[J].
测绘技术装备,2013,15(4) : 25–28.
Jiao Lifen. Distribution, Density, Accuracy and Transformation Accuracy Analysis of Coincidence Point Based on Coordinate Transformation[J]. Geomatics Technology and Equipment,2013,15(4) : 25–28. |
| [6] |
李东, 毛之琳, 廖文兵, 等. CGCS2000与独立坐标系转换模型适用性研究[J].
测绘工程,2015,24(1) : 1–5.
Li Dong, Mao Zhilin, Liao Wenbin, et al. Applicability Research of Transformation Model Between CGCS2000 and Independent Coordinate System[J]. Engineering of Surveying and Mapping,2015,24(1) : 1–5. |
| [7] |
陈俊勇. 中国现代大地基准——中国大地坐标系统2000(CGCS2000)及其框架[J].
测绘学报,2008,7(3) : 269–271.
Chen Junyong. Chinese Modern Geodetic Datum—Chinese Geodetic Coordinate System 2000(CGCS 2000) and Its Frame[J]. Acta Geodaetica et Cartographics Sinica,2008,7(3) : 269–271. |
| [8] |
杨元喜, 徐天河. 不同坐标系综合变换法[J].
武汉大学学报·信息科学版,2001,26(6) : 509–513.
Yang Yuanxi, Xua Tianhe. The Combined Method of Datum Transformation Between Different Coordinate Systems[J]. Geomatics and Information Science of Wuhan University,2001,26(6) : 509–513. |
| [9] |
王文利, 程传录, 陈俊英. 常用坐标转换模型及其实用性研究[J].
测绘信息与工程,2010,35(5) : 37–39.
Wang Wenli, Cheng Chuanlu, Chen Junying. Coordinate Transformation Models and Their Practicability[J]. Journal of Geomatics,2010,35(5) : 37–39. |
| [10] |
鲍建宽, 李永利, 李秀海. 大地坐标转换模型及其应用[J].
测绘工程,2013,22(3) : 56–60.
Bao Jiankuan, Li Yongli, Li Xiuhai. Geodetic Coordinate Transformation Model and Its Application[J]. Engineering of Surveying and Mapping,2013,22(3) : 56–60. |
 2016, Vol. 41
2016, Vol. 41

