| 基于机器视觉的桥梁挠度实时精密测量方法 |
2. 空间信息智能感知与服务深圳市重点实验室,广东 深圳,518060;
3. 广东省城市空间信息工程重点实验室,广东 深圳,518060;
4. 自然资源部大湾区地理环境监测重点实验室,广东 深圳,518060;
5. 西安敏文测控科技有限公司,陕西 西安,710199
2. Shenzhen Key Laboratory of Spatial Smart Sensing and Services, Shenzhen University, Shenzhen 518060, China;
3. Guangdong Key Laboratory of Urban Informatics, Shenzhen University, Shenzhen 518060, China;
4. Key Laboratory for Geo-Environmental Monitoring of Great Bay Area, Ministry of Natural Resources, Shenzhen 518060, China;
5. Xi'an Min-Win M & C Technology. Co., Ltd., Xi'an 710199, China
桥梁跨越河流、峡谷等地理障碍,保障交通网络连通性,它是重要的交通基础设施。随着使用时间的增长,桥梁承受荷载的能力不断下降,到一定程度就会影响到桥梁安全性能,导致桥梁损坏甚至倒塌事故,造成严重的人民生命财产安全损失[1]。确保桥梁安全运营一直是交通部门重点关注的问题。集成传感器、物联网(internet of things, IoT)、全球导航卫星系统(global navigation satellite system, GNSS)技术进行桥梁结构健康监测,获取桥梁沉降或局部结构形变信息,可为桥梁安全性和使用性能的评估提供依据[2-4]。桥梁在荷载作用或温度变化下,其轴线在铅锤线方向会发生变形,此变形被称为桥梁挠度。桥梁挠度测量是桥梁结构健康监测的重要内容,可通过精准的桥梁挠度数据来监测桥梁荷载的时变规律,揭示桥梁形变的周期性规律,分析桥梁整体结构安全性[5, 6]。
随着测量、传感器和计算机技术的进步,相关学者研究了多种桥梁挠度测量的方法,分为水准测量法和自动化法两大类[5-11]。水准测量法在桥面上选择若干监测点,定期进行监测点的高精度水准测量,从而反映主梁的长周期的挠度,测量精度可达到0.5 mm。但是该方法费时费力,实时性差[12]。
自动化的桥梁挠度测量方法包括倾角仪、连通管法、GNSS、测量机器人、激光图像测量法、地面微波干涉雷达等。其中,倾角仪法沿桥梁轴线方向在桥面若干位置处布设倾角仪,利用测点处的倾角值计算桥梁挠度曲线[12]。连通管法沿主梁布设连通管,根据连通管内液面水平的原理,观测桥面若干测点处连通管内的液面高度,从而计算桥面的形变值,监测桥梁挠度变化。连通管法原理简单,成本低,实现方便,精度相对较高,并且可以多点同步监测[13]。GNSS测量法在桥梁附近处固定不动的参考点上设置基准站,在桥梁选取若干变形监测点,设置GNSS移动站,进行实时/后处理差分测量,获取监测点的位移。GNSS测量法不受通视条件的影响,测量精度一般在厘米级[14-16]。测量机器人由步进马达驱动,按照设计的程序依次扫描桥梁上的形变测点,获取这些点的精确位置,从而计算桥梁挠度。该方法具有快速监测、量程大、精度高等特点,但不能进行多点同步监测[17-21]。激光图像测量法在桥梁的测点上安装激光发射源或目标靶,利用激光的准直性,计算激光投影点的坐标,精准地推算桥梁挠度值[22-30]。激光图像测量法需要考虑镜头畸变、大气湍流引起的误差。地面微波干涉雷达结合步进频率连续波技术、合成孔径雷达技术和干涉测量技术,实现了高精度、非接触式、远距离监测的桥梁挠度精准测量[31-39]。
本文提出了一种基于视觉的动态桥梁挠度实时监测方法,在桥梁相对稳定处(如桥墩)安装红外相机和基准靶标,在桥板下的若干测量点处安装测量靶标。通过观测测量靶标相对基准靶标在像平面上的相对移动,实现桥梁挠度的实时高精度测量。特别地,利用基准靶标能够有效抑制图像系统噪声和大气变化等因素造成的误差。本文方法与传统的千分尺测量法的测量结果具有高度的一致性,相关系数高达0.95,测量值相差仅为0.2 mm,能够满足桥梁高精度形变实时监测的需要。本文方法可用于大型桥梁、桥梁集群的结构健康监测,为桥梁安全性能精准评估提供数据支撑。
1 桥梁挠度机器视觉测量原理基于机器视觉的桥梁动态挠度监测方法在主梁和桥墩处分别安装测量靶标和红外相机,采用红外相机对基准靶标和测量靶标同时进行观测,根据几何关系,计算像平面上测量靶标相对于基准靶标的实际位移,从而测量桥板上待测点处的实时形变。
桥梁动态挠度测量系统中的基准靶标和测量靶标采用850 nm红外LED灯,克服环境光的影响。基准靶固定在相对静止的参考点处,目标靶则固定在桥板下待测点处,将基准靶、目标靶成像在摄像机的长焦光学系统图像传感器上,如图 1所示。相机传感器通过稳定机械装置固定在基准点上,例如盖梁等位置,即使在重型车等荷载的作用下也能保持位置不发生变化。调节相机的参数和图像采集频率,采集目标部位不同时间的图像。随着桥梁结构在温度和荷载的作用下发生变形,目标靶在相机坐标系中会呈现出不同的像素坐标。利用嵌入式处理平台,进行图像识别并定位靶标的中心,确定基准靶和目标靶的像素坐标。最后,根据单像素代表的实际距离,由物像关系确定目标靶与基准靶之间的相对空间位置,从而计算得到挠度值,实现桥梁动态挠度的实时监测。
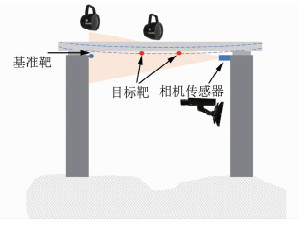 |
| 图 1 桥梁动态挠度机器视觉测量原理 Fig.1 Principle of Monitoring the Deflection of the Bridge Using Computer Vision |
2 桥梁挠度计算方法
通过相机拍摄已安装的基准靶标和测量靶标采集到图像数据后,需要对原始图像数据进行处理,计算实时的桥梁挠度。
图像数据处理流程如图 2所示。首先进行图像二值化和中值滤波,提取图像中基准靶标和目标靶标对应光斑的边缘特征;然后分别计算其对应中心点像素的坐标;最后通过物像关系来计算桥梁动态挠度值。
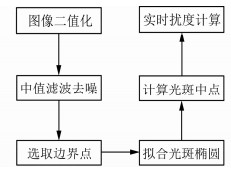 |
| 图 2 图像数据处理流程图 Fig.2 Flow Chart of the Image Data Processing |
2.1 靶标中心识别
首先,将相机采集到的图片转换为灰度图像,并利用式(1)对其进行二值化。
| ${\rm{G}}\left( {x,y} \right) = \left\{ {\begin{array}{*{20}{c}} {255,f\left( {x,y} \right) \ge T}\\ {0,f\left( {x,y} \right) < T} \end{array}} \right\}$ | (1) |
式中,G(x, y)为二值化图像;f(x, y)为原图像;x, y为像素坐标;T为设定的阈值。图像二值化后,对结果使用中值滤波去噪,将区域中的像素按灰度级排列,以中间值为输出对象,从而提高轮廓信息的提取精度。
图像中提取的光斑往往呈现椭圆形,而非规则的圆形。因此,采用椭圆拟合方法求取光斑中心像素坐标,计算如下:
| $f\left( {x, y} \right) = A{x^2} + Bxy + C{y^2} + Dx + Ey + F = 0$ | (2) |
式中,A、B、C、D、E、F为椭圆方程系数,且A+C≠0。令A+C=1,则A=1-C,通过最小二乘法求解椭圆方程系数,计算椭圆中心点(xc, yc):
| $\left\{ {\begin{array}{*{20}{c}} {{x_c} = \frac{{BE - 2CD}}{{\begin{array}{*{20}{c}} {4AC - {B^2}} \end{array}}}}\\ {{y_c} = \frac{{BD - 2AE}}{{\begin{array}{*{20}{c}} {4AC - {B^2}} \end{array}}}} \end{array}} \right.$ |
需要6个边界像素点(xi, yi), i=1, 2, 3,…, 6求解椭圆方程系数。为了消除随机选点的偶然性影响,本文采取多次随机选取边界点对椭圆光斑进行拟合,从而确定最优拟合参数。设(xi, yi)到f(x, y)的残差平方和为:
| $\begin{array}{*{20}{c}} {\left( {A,B,C,D,E,F} \right) = }\\ {\sum\limits_{i = 1}^n ( Ax_i^2 + B{x_i}{y_i} + Cy_i^2 + D{x_i} + E{y_i} + F{)^2})} \end{array}$ | (3) |
对其求偏导:
| $\frac{{\partial f}}{{\partial A}} = \frac{{\partial f}}{{\partial B}} = \frac{{\partial f}}{{\partial C}} = \frac{{\partial f}}{{\partial D}} = \frac{{\partial f}}{{\partial E}} = \frac{{\partial f}}{{\partial F}} = 0$ |
则所求极值点为残差平方和的最小值。本文通过多次选取边界点,计算各像素点与椭圆的残差平方和,输出小于阈值残差平方和的像素点。经过多次求解拟合像素点,以输出次数最多的像素点拟合最优椭圆,并根据其求解出椭圆中心点像素坐标(xc, yc)。
利用式(1)~式(3),分别计算基准靶标和测量靶标的像素中心坐标。
2.2 实时挠度计算获取靶标的图像光斑中心点像素坐标后,通过计算目标靶标与基准靶标之间的相对位移,得到桥梁的实时挠度值,计算过程如下:
1) 根据靶标中心识别算法,分别计算基准靶标和目标靶标的图像光斑中心点像素坐标(xc, yc),(x′c, y′c)。
2) 计算两者之间的像素距离:
3) 根据已知的像元大小d,求得两个靶标中心点在图像上的实际距离,即ΔH=d×Δh。
4) 图 3为相机成像示意图,根据其中的物像关系计算桥梁挠度挠度目标点处的实际位移:
| $\Delta y = \frac{{L' \times \Delta {\rm{H}}}}{f}$ | (4) |
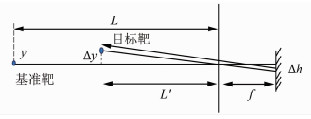 |
| 图 3 相机成像示意图 Fig.3 The Schematic Diagram of Camera Imaging |
式中,L′为目标靶标到相机的距离;f为相机焦距。
5) 考虑到目标靶标与基准靶标之间存在初始位移Δh′,在计算挠度时应去除初始位所带来的误差,因此挠度的实际变化值为:
| $\Delta y = \frac{{L' \cdot \left( {\Delta H - \Delta {H^{\rm{'}}}} \right)}}{f}$ | (5) |
式中,ΔH′=d×Δh′。
通过目标靶标与基准靶标之间的相对位移计算桥梁挠度,能够有效抑制图像系统噪声和大气变化等因素造成的误差,从而有效提高桥梁挠度的测量精度。
2.3 桥梁挠度异常探测利用高精度、高频率的桥梁挠度测量数据进行异常探测,预警威胁桥梁安全的异常事件。然而,温度、湿度等环境因素变化导致桥梁形变呈现昼夜周期性变化,干扰桥梁挠度的异常探测。本文采用滑动窗口法,选择一段时间内的桥梁挠度数据进行异常探测。假定当前时刻为t1,选择时间窗口t0~t1内的挠度测量值vt,构成集合V={vt, t0 < t≤t1}。计算集合内的挠度测量均值Ev和方差σv,将区间[Ev-3σv, Ev+3σv]之外的挠度值识别为异常值。进一步地利用异常值触发桥梁安全预警系统,驱动桥面上的相机联动拍照,并通过移动互联网发出警告信息。
3 实验分析及应用为了验证基于机器视觉的桥梁动态挠度实时测量的精度。在某市政桥梁上安装桥梁动态挠度视觉测量系统,采集实验数据并进行分析。将本文方法的测量结果与千分尺测量方法进行比较,分析两者之间的一致性与差异。最后,集成边缘计算、智能网关和互联网地图,开发桥梁结构健康监测系统,实现桥梁动态挠度的实时在线监测。
3.1 实验结果在某市政桥梁上安装本文研发的桥梁动态挠度测量系统,在两个桥墩处分别安装测量相机和基准靶,在桥跨中安装目标靶,测量目标靶处的实时挠度值。系统布置如图 4所示。同时,在目标靶标位置处安装细钢丝,下坠重锤,将桥面形变传递至地面,并利用高精度千分尺测量重锤的高度变化,从而精准测量目标靶处的形变位移,并将其与本文视觉测量的结果进行比较。
 |
| 图 4 桥梁挠度测量系统安装 Fig.4 The Installation of the Bridge Deflection Measurement System |
图 5为两种方法的测量结果。可以发现,无车辆通过时,主梁受温度影响,存在固有形变,约为2.4 mm,由于桥梁受到车辆载荷的影响,桥梁表面会发生形变,其值约为-6.0~4.8 mm。其中车辆通过时,形变值会先减少后增加,这是因为车辆逐渐接近待测点,由于载荷影响,在车辆前方会让桥面向上发生形变,形成一个局部的波峰。当车辆通过时,受重力作用,桥面会向下发生形变,车辆的形变达到最大,形成一个局部的波谷。在小型车通过时,由于小型车自重较轻,主梁的位移量较小,在北京时间13:40左右的形变约为-3.0~0.0 mm。重型车通过时,由于其自重较大,桥梁的形变随之增大,在北京时间13:40左右的瞬时位移量为可达-6.0 mm。
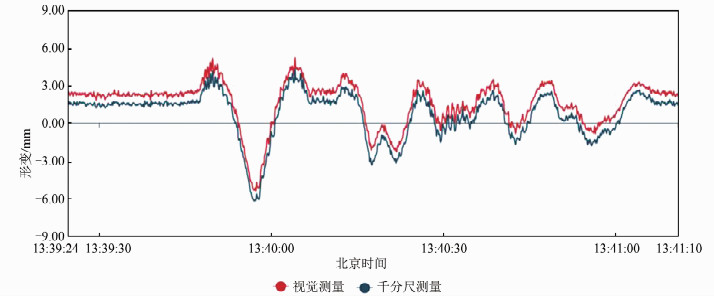 |
| 图 5 两种方法的桥梁挠度测量结果 Fig.5 The Bridge Deflection Measuring Results of Two Methods |
比较视觉方法和千分尺方法的计算结果,可以发现,整体上看,两者给出的挠动值的波动趋势十分相似。计算其皮尔逊相关系数,结果高达0.95。然后,计算其差值并进行统计。结果表明,两者差值的均值为0.2 mm,中误差为0.38 mm。因此,本文的机器视觉测量方法和经典的千分尺方法高度一致,精确度高。
利用桥梁的实时挠度精确测量值,还能够计算桥梁上车辆通行量。图 6以该桥梁2020-11-03北京时间21:00-22:00的挠度测量值为例,给出了桥梁挠度的变化曲线。可以发现,在短时间内,无车辆通过时,桥梁的挠度值变化较小,该桥梁在21:00-22:00的挠度值稳定在-2.00 mm左右。高频率的视觉测量挠度值的变化能够反映车辆通过桥梁的情况。通过滤波算法提取挠度信号中的波形,统计车辆数量。结果表明,在2020-11-03北京时间21:00-22:00内,共有95辆机动车通过该桥梁,其中小型车65辆,大型车30辆。
 |
| 图 6 某小时的桥梁挠度值变化情况 Fig.6 The Change of Bridge Deflection in One Hour |
桥梁形变不仅受到车辆载荷的影响,还与环境中的温度、大气紧密相关。利用长周期的桥梁挠度变化值,可以发现温度、大气等变化对桥梁形变的影响。图 7给出了该桥梁在某一天中该桥梁挠度值变化情况。可以发现,桥梁挠度在一天中不断变化。在夜间,由于温度较低,桥梁的形变较小,大部分时段的桥梁挠度值在2.05 mm左右。在中午时段,桥梁的挠度值逐渐增大,在3.0 mm左右。在下午时段,桥梁挠度值不断减小,接近2.0 mm。在晚间,桥梁挠度值在1.8 mm附近波动。
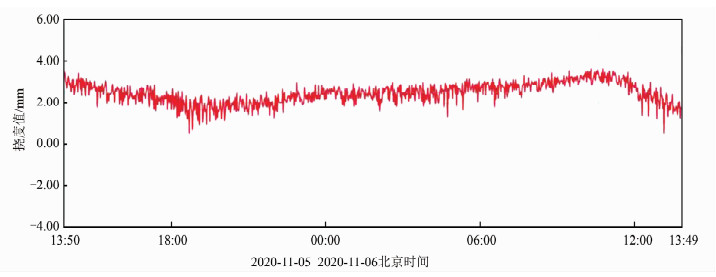 |
| 图 7 某一天中的桥梁挠度值变化情况 Fig.7 The Change of Bridge Deflection in One Day |
3.2 典型应用
本文基于互联网地图信息服务和建筑物信息模型(building information model, BIM), 结合边缘计算和空间可视化技术,进行桥梁挠度实时监测数据的接入与可视化,开发了桥梁结构健康监测系统如图 8所示。
 |
| 图 8 集成GIS和边缘计算的桥梁结构健康监测系统 Fig.8 The Structure Health Monitoring System of Bridges Integrating GIS and Edge Computing |
传统的结构健康监测系统一般通过3G/4G移动网络或者有线互联网将监测数据传回监测中心,数据量大,网络传输负担重,可连接的传感器数量十分有限。边缘计算在传感器端就进行少量计算任务,感知结果通过网络传输回监测中心,避免了大体量的数据传输。本文基于ARM(advanced RISC machines)平台实现桥梁挠度的实时计算。在相机端先进行挠度计算,然后将计算结果传输回云平台,这样将传输内容从图像转变为挠度值,可极大减少数据的传输量。
图 9为桥梁动挠度数据分析模块的主要界面。该模块包括实时数据、效应曲线和统计比对3个功能。其中实时数据部分接入动挠度数据并绘制变化曲线;效应曲线部分分析挠度变化与动应变监测之间的关系;统计比对部分分析长周期的桥梁动态挠度值,利用时间序列分析,统计其变化规律,发现桥梁挠度异常值。根据挠度异常检测的结果,能够进行桥梁安全预警。图 10为某桥梁异常值驱动的重型车辆抓拍界面。可以发现,该系统能够及时发现桥梁剧烈形变,从而进行预警。
 |
| 图 9 桥梁动挠度数据分析模块主要界面 Fig.9 Main Interface of the Dynamic Deflection of Bridges Analysis Module |
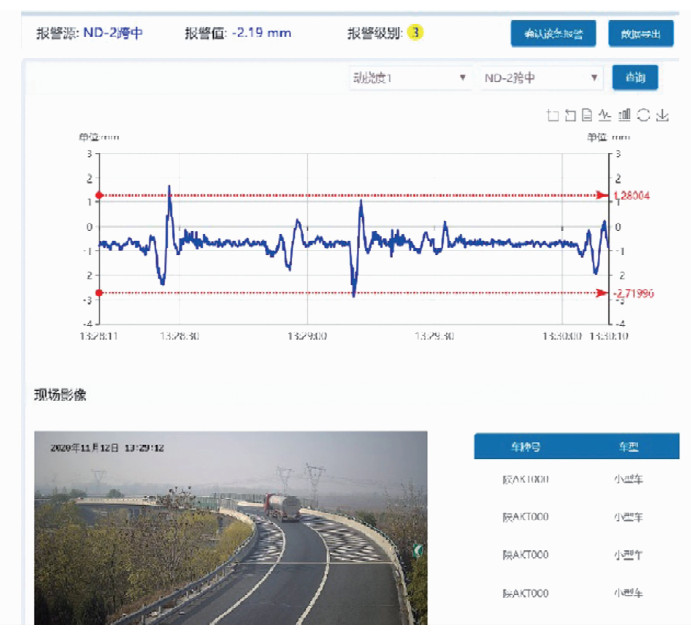 |
| 图 10 基于桥梁挠度值的超重型车辆抓拍界面 Fig.10 The Interface of Superheavy Vehicles Candid Photos Based on the Bridges Deflection |
目前,该桥梁结构健康监测系统已经在武汉、南京、合肥、济南、北京等地广泛使用,实时监测了多起桥梁挠度异常情况,并抓拍了多起超重型车辆的通行过程,效果良好。
4 结束语桥梁挠度刻画了荷载作用或者温度变化下的桥梁几何形变。桥梁挠度测量是桥梁结构健康监测的重要内容,精准的桥梁挠度数据可以用来监测桥梁荷载的时变规律,揭示桥梁形变的周期性规律,分析桥梁整体结构安全性。本文提出了基于机器视觉的动态桥梁挠度实时监测方法,利用高精度相机和若干红外靶标测量桥梁上待测点处的实时形变。其中基准靶标能够消除温度、湿度等环境变化的影响,实现桥梁挠度的实时高精度测量,测量精度可达到0.2 mm。本文方法可进一步推广应用于大型桥梁、桥梁集群的结构健康监测,为桥梁安全性能精准评估提供数据支撑。
| [1] |
Li H, Ou J P. Structural Health Monitoring: From Sensing Technology Stepping to Health Diagnosis[J]. Procedia Engineering, 2011, 14(1): 753-760. |
| [2] |
Jung J, Kim D, Suresh K P V. Long Term Deflection Monitoring of Cable-Stayed Bridge Using Time-Series Interferometry[C]. 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 2018
|
| [3] |
杜彦良, 苏木标, 刘玉红, 等. 武汉长江大桥长期健康监测和安全评估系统研究[J]. 铁道学报, 2015, 37(4): 101-110. |
| [4] |
杨李东, 钱志坚. 基于物联网与GIS的城市桥梁健康监测系统设计[J]. 测绘地理信息, 2019, 44(4): 19-22. |
| [5] |
路双, 张永水. 桥梁健康监测挠度评估方法应用[J]. 重庆交通大学学报(自然科学版), 2013, 32(6): 1 133-1 136. |
| [6] |
魏斌, 王强. 大跨度桥梁挠度监测方法评述[J]. 中外公路, 2015, 35(6): 164-169. |
| [7] |
文雪中. 大型桥梁挠度监测的方法比较及实践[J]. 测绘地理信息, 2016, 41(5): 70-73. |
| [8] |
Yu S S, Zhang J. Fast Bridge Deflection Monitoring Through an Improved Feature Tracing Algorithm[J]. Computer-Aided Civil and Infrastructure Engineering, 2020, 35(3): 292-302. DOI:10.1111/mice.12499 |
| [9] |
邓海. 桥梁结构挠度理论分析和健康监测研究[J]. 建筑技术, 2016, 47(11): 1 021-1 023. |
| [10] |
龚颖男. 基于挠度及有效预应力分析的高墩大跨度桥梁施工测量技术研究[J]. 城市勘测, 2020(3): 170-172. |
| [11] |
孙丰春. 大跨径桥梁挠度变形监测技术应用实践[J]. 海洋测绘, 2020, 40(4): 77-82. |
| [12] |
张俊中, 朱义朝, 刘乾, 等. 基于全站仪在桥梁挠度检测中的应用和研究[J]. 测绘与空间地理信息, 2019, 42(1): 41-44. |
| [13] |
刘龑, 王文剑, 李波, 等. 基于MEMS倾角仪的桥梁挠度监测动态及长期性能研究[J]. 中外公路, 2020, 40(4): 174-178. |
| [14] |
曾威, 于德介, 胡柏学, 等. 基于连通管原理的桥梁挠度自动监测系统[J]. 湖南大学学报:自然科学版, 2007(7): 44-47. |
| [15] |
安庆, 江博, 吴树森. 基于GNSS和传感技术的桥梁安全监测系统设计[J]. 全球定位系统, 2016, 46(5): 107-112. |
| [16] |
余加勇, 邵旭东, 晏班夫, 等. 基于全球导航卫星系统的桥梁健康监测方法研究进展[J]. 中国公路学报, 2016, 29(4): 30-41. |
| [17] |
余加勇. 基于GNSS和RTS技术的桥梁结构健康监测[J]. 测绘学报, 2015, 44(10): 1 177. |
| [18] |
徐进军, 郭鑫伟, 廖骅, 等. 基于地面三维激光扫描的桥梁挠度变形测量[J]. 大地测量与地球动力学, 2017, 37(6): 609-613. |
| [19] |
欧阳俊峰.基于三维激光扫描技术的现役桥梁变形监测应用研究[D].广州: 华南理工大学, 2018
|
| [20] |
骆义, 赵文举, 张建. 基于三维激光扫描技术的桥梁检测应用研究[J]. 智能建筑与智慧城市, 2020(3): 14-18. |
| [21] |
吴涛, 陈勇, 赵斌. 三维激光扫描技术在大型桥梁结构健康监测中的应用研究[J]. 上海公路, 2019(2): 71-74. |
| [22] |
赵宏伟, 宋云峰, 王会峰, 等. 激光基准桥梁挠度成像检测系统[J]. 激光与红外, 2019, 49(3): 282-290. |
| [23] |
蔡友发, 傅星, 李飞. 数字图像相关方法的桥梁挠度仪的温度补偿[J]. 电子测量与仪器学报, 2019, 33(7): 88-92. |
| [24] |
赵雪丹.基于DM642的激光基准桥梁挠度图像式检测仪[D].西安: 长安大学, 2017
|
| [25] |
张奔牛, 李星星, 宋军, 等. 激光投射式位移传感技术在桥梁挠度检测中的应用研究[J]. 传感技术学报, 2009, 22(5): 755-759. |
| [26] |
董萼良, 黄跃平, 何小元, 等. 桥梁静载试验中梁截面挠度的激光测试方法[J]. 桥梁建设, 2006(1): 70-72. |
| [27] |
董辉, 陈伟民, 符欲梅, 等. 一种激光图像挠度测量方法[J]. 传感器技术, 2004(10): 63-65. |
| [28] |
Vicente M A, Gonzalez D C, Minguez J, et al. A Novel Laser and Video-Based Displacement Transducer to Monitor Bridge Deflections[J]. 2018, 18, doi: 10.3390/s18040970
|
| [29] |
黄声享, 罗力, 何超. 地面微波干涉雷达与GPS测定桥梁挠度的对比试验分析[J]. 武汉大学学报·信息科学版, 2012, 37(10): 1 173-1 176. |
| [30] |
刘春, 程起军, 李俊义, 等. 基于地基干涉雷达的大型桥梁动态挠度监测与分析[J]. 工程勘察, 2017, 45(1): 53-58. |
| [31] |
Gentile C, Bernardini G. An Interferometric Radar for Non-Contact Measurement of Deflections on Civil Engineering Structures: Laboratory and Full-Scale Tests[J]. Structure and Infrastructure Engineering, 2010, 6(5): 521-534. DOI:10.1080/15732470903068557 |
| [32] |
罗剑. 地面干涉雷达技术在公路桥梁动态检测中的应用[J]. 工程与建设, 2019(4): 564-566. |
| [33] |
刘明亮, 丁克良, 宋子超, 等. 结合地基微波雷达与GPS的大型桥梁挠度检测分析[J]. 北京测绘, 2019(8): 924-928. |
| [34] |
谢润. 非接触式雷达IBIS-S遥测系统在桥梁挠度影响线监测中的应用研究[J]. 华东公路, 2019(1): 99-102. |
| [35] |
卢钊. GB-SAR城市桥梁动挠度监测大气参数优化改正[D].北京: 北京建筑大学, 2019
|
| [36] |
刘德煜. GPS与微波干涉测量在桥梁动挠度测量中的对比分析[J]. 桥梁建设, 2009(3): 81-84. |
| [37] |
刘小阳, 孙广通, 李峰, 等. 基于地基雷达的高铁简支箱梁运营性能检定[J]. 中国铁道科学, 2020, 41(1): 50-56. |
| [38] |
王鹏, 邢诚, 项霞. 地基干涉雷达IBIS-S桥跨结构振动变形测量与模态分析[J]. 测绘通报, 2019(10): 35-39. |
| [39] |
徐亚明, 王鹏, 周校, 等. 地基干涉雷达IBIS-S桥梁动态形变监测研究[J]. 武汉大学学报·信息科学版, 2013, 38(7): 845-849. |
 2020, Vol. 45
2020, Vol. 45

