| GPS广域增强系统星历和星钟改正及用户性能分析 |
2. 武汉大学卫星导航定位技术研究中心,湖北 武汉,430079;
3. 千寻位置网络有限公司,上海,200438;
4. 武汉大学地球空间环境与大地测量教育部重点实验室,湖北 武汉,430079
2. GNSS Research Centre, Wuhan University, Wuhan 430079, China;
3. Qianxun SI CO., Ltd., Shanghai 200438, China;
4. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
全球卫星导航定位系统广泛应用于测绘、授时、航空航天等多个领域,尤其在民用航空领域发挥着重要的作用,但由于卫星广播星历的精度有限且完备性告警时延太长,造成精度和安全性能要求较高的领域(如飞机的精密进近阶段的导航性能)不能满足要求。因此,为了提高全球导航卫星系统(global navigation satellite system, GNSS)的性能,诸多学者提出了多种差分系统,如广域差分系统。
目前,国内外很多学者对广域增强系统星历和星钟差分改正数算法作了大量的研究[1-10],并且很多国家也已经建立了自己的广域增强系统,如美国对GPS的广域增强系统(wide area augmentation system, WAAS);欧洲对GPS GLONASS的增强系统(European geostationary navigation overlay service,EGNOS);日本的多功能GPS卫星增强系统(multi-functional satellite augmentation system,MSAS)和准天顶卫星增强系统(quasi-zenith satellite system,QZSS);俄罗斯的GLONASS差分矫正和监测系统(system for differential corrections and monitoring,SDCM)等。国内对于广域增强系统的算法研究不多,李孝辉等[5]通过矢量差分的方法来计算GPS卫星星历及星钟差分改正数,但这种方法的实验数据主要是通过仿真得到,且没有分析卫星故障情况下的完备性;Chen等[7]实现了广域增强系统的矢量差分算法,并用实测数据对精度进行了分析,使用超快速精密星历作为先验参数,提高了差分改正数精度,但其主要应用于双频伪距观测值,没有对卫星故障情况下的完备性监测进行分析;陈金平等[8, 9]分析了广域增强系统和用户站的完备性监测情况,但没有涉及差分改正数的矢量差分算法。
本文从GNSS广域增强系统的矢量差分改正和故障监测两个方面开展较为全面的研究与性能分析,为中国北斗广域增强系统的研究与建设提供参考。
1 星历及星钟差分改正算法本文采用矢量差分的方法来求解卫星星历及星钟差分改正数[11-15],主要包括数据预处理、参考站接收机钟差求解、星历差分改正数求解、星钟差分改正数求解几个部分。
1.1 数据预处理数据预处理主要包括:周跳的探测[16],双频载波相位观测值平滑伪距和电离层[2],对流层改正、几何距离与卫星广播星历钟差计算,伪距残差计算。在此基础上,可以得到伪距残差Δρkj及其方差σΔρkj2为:
| $ \left\{ \begin{array}{l} \Delta \rho _k^j = \rho _k^j - D_k^j - I_k^j - T_k^j + {B^j} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{l}}_k^j\Delta {\mathit{\boldsymbol{R}}^j} + {b_k} - \Delta {B^j} + v_k^j\\ \sigma _{\Delta \rho _k^j}^2 = \sigma _{\rho _k^j}^2 + \sigma _{I_k^j}^2 + \sigma _{T_k^j}^2 \end{array} \right. $ | (1) |
式中,ρkj为平滑伪距观测值;Dkj为由广播星历计算得到的卫星至参考站的几何距离;Ikj为双频平滑电离层改正值;Tkj为对流层改正值;ΔRj与ΔBj分别为卫星j的星历误差、星钟误差;bk为参考站k的接收机钟差;lkj为卫星至接收机的单位向量;vkj为伪距残差观测值的观测噪声;σρkj为平滑伪距测量噪声中误差;σTkj为对流层改正中误差;σIkj为平滑电离层改正中误差。
1.2 参考站接收机钟差求解参考站接收机钟差的求解主要分为主控站接收机钟差计算和共视时间转换两个步骤。其中主控站接收机钟差为整个系统提供时间基准,而共视时间转换将所有的接收机钟差统一到这一时间基准上[2]。式(1)中的主控站接收机钟差可根据可见卫星的伪距残差经过加权平均(即最小二乘)估计得到,其估计值和方差分别为:
| $ \left\{ \begin{array}{l} {{\hat b}_M} = \left( {\sum\limits_{j = 1}^N \frac{{\Delta \rho _M^j}}{{\sigma _{\Delta \rho _M^j}^2}} } \right) \times \sigma _{{{\hat b}_{_M}}}^2\\ \;\;\;\sigma _{{{\hat b}_{_M}}}^2 = {\left( {\sum\limits_{j = 1}^N {\frac{1}{{\sigma _{\Delta \rho _M^j}^2}}} } \right)^{ - 1}} \end{array} \right. $ | (2) |
式中,N为参考站与主控站共视卫星的个数。
可以看出加权平均估计得到的主控站接收机钟差受到星历、星钟误差以及其他残差的影响,但主控站接收机钟主要用来提供一个时间基准,且这些影响通过共视时间转换也会反映在其他卫星上。将参考站上的时间与主控站的时间统一,求得参考站与主控站之间接收机钟差之差
| $ {\hat b_k} = {\hat b_M} + \Delta {\hat b_{k, M}} $ | (3) |
为了求得
| $ \begin{array}{l} \Delta \rho _{k, M}^j = \Delta \rho _k^j - \Delta \rho _M^j = \\ (\mathit{\boldsymbol{l}}_k^j - \mathit{\boldsymbol{l}}_M^j)\Delta {\mathit{\boldsymbol{R}}^j} + \Delta {b_{k, M}} + v_{k, M}^j \end{array} $ | (4) |
与式(1)相比,式(4)消除了卫星钟差ΔBj的影响;由于广域增强系统为一个区域网,卫星至参考站和主控站的单位向量之差非常小,最大仅几个厘米,(lkj-lMj)ΔRj可忽略不计[2]。故Δbk, M也可以采用估计主控站接收机钟的方法通过加权最小二乘估计得到。
1.3 卫星星历差分改正和故障监测经时间同步处理之后,所有参考站的伪距残差均统一到同一个时间基准上。因此,可逐颗卫星独立求解其星历及星钟差分改正数。时间同步后的伪距残差观测值及其方差可简写为:
| $ \left\{ \begin{array}{l} \Delta \tilde \rho _k^j = \Delta \rho _k^j - {{\hat b}_k} = \mathit{\boldsymbol{l}}_k^j\Delta {\mathit{\boldsymbol{R}}^j} - \Delta {B^j} + v_k^j\\ \sigma _{\Delta \tilde \rho _k^j}^2 = \sigma _{\Delta \rho _k^j}^2 + \sigma _{\Delta {{\hat b}_{k, M}}}^2 + \sigma _{\Delta {{\hat b}_M}}^2 \end{array} \right. $ | (5) |
式(5)的右边同时包含有卫星钟改正误差ΔBj与星历误差ΔRj。为了消除ΔBj,需要选择一个接收机钟差方差最小的参考站为基准站ref,然后在参考站k与基准站ref的伪距残差观测值之间求单差,得到:
| $ z_k^j = \Delta \tilde \rho _k^j - \Delta \tilde \rho _{{\rm{ref}}}^j = (\mathit{\boldsymbol{l}}{}_k^j - \mathit{\boldsymbol{l}}_{{\rm{ref}}}^j)\Delta {\mathit{\boldsymbol{R}}^j} + \mathit{\boldsymbol{\varepsilon}} _{k, {\rm{ref}}}^j $ | (6) |
式中,εk, refj为随机误差;ΔRj为:
| $ \Delta {\mathit{\boldsymbol{R}}^j} = {\left[ {\Delta {X^j}\;\;\;\Delta {Y^j}\;\;\;\Delta {Z^j}} \right]^{\rm{T}}} $ | (7) |
为了求得卫星的轨道误差ΔRj,将基准站ref与多个参考站(k=1, 2, …, n)依次差分后可以得到多个如式(6)的方程,表示为矩阵形式为:
| $ \mathit{\boldsymbol{z}} = \mathit{\boldsymbol{H}}\Delta {\mathit{\boldsymbol{R}}^j} + \mathit{\boldsymbol{\varepsilon }} $ | (8) |
式中,z=[z1j, …, znj];H为被估计参数的系数矩阵,即设计矩阵;ε为相互独立的随机误差向量,其对应的方差矩阵为D。基于以上模型,可以得到ΔRj的最小二乘估计。
由于被估计参数ΔRj有先验的统计信息,根据经验可知:ΔRj的期望接近零,中误差约为2 m左右,所以本文在对其估计中加入这些先验统计信息:E(ΔRj)=0和方差DΔRj。利用这些先验统计信息,可以对ΔRj进行最小方差估计为:
| $ \Delta {\mathit{\boldsymbol{\hat R}}^j} = {\mathit{\boldsymbol{D}}_{\Delta {\mathit{\boldsymbol{R}}^j}}}\mathit{\boldsymbol{H}}{({\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{D}}_{\Delta {\mathit{\boldsymbol{R}}^j}}}\mathit{\boldsymbol{H}} + \mathit{\boldsymbol{D}})^{ - 1}}\mathit{\boldsymbol{z}} $ | (9) |
| $ {\mathit{\boldsymbol{D}}_{\Delta {{\mathit{\boldsymbol{\hat R}}}^j}}} = {\mathit{\boldsymbol{D}}_{\Delta {\mathit{\boldsymbol{R}}^j}}} - {\mathit{\boldsymbol{D}}_{\Delta {\mathit{\boldsymbol{R}}^j}}}{\mathit{\boldsymbol{H}}^{\rm{T}}}{(\mathit{\boldsymbol{H}}\;{\mathit{\boldsymbol{D}}_{\Delta {\mathit{\boldsymbol{R}}^j}}}{\mathit{\boldsymbol{H}}^{\rm{T}}} + \mathit{\boldsymbol{D}})^{ - 1}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{D}}_{\Delta {\mathit{\boldsymbol{R}}^j}}} $ | (10) |
采用最小方差估计不仅利用了轨道误差的先验信息,而且可以有效地克服原来最小二乘估计中HTDΔRj-1H可能出现奇异的情况。
广域增强系统不仅发布差分改正,而且也对差分改正信息进行实时监测以确保其完备性。监测方法是对其改正结果进行卡方检验。假设检验量为:
| $ \left\{ \begin{array}{l} T = \sum\limits_{k = 1}^{k = n} {\frac{{{{\left( {z_k^j - (\mathit{\boldsymbol{l}}_k^j - \mathit{\boldsymbol{l}}_m^j)\Delta {{\mathit{\boldsymbol{\hat R}}}^j}} \right)}^2}}}{{\sigma _i^2}}} \\ 原假设\left( {无故障} \right)为:T \sim {\chi ^2}\left( {\lambda = 0, n - 3} \right)\\ 备选假设为:T \sim {\chi ^2}\left( {\lambda \ne 0, n - 3} \right) \end{array} \right. $ | (11) |
式中,λ为卡方分布的非中心化参数;n为观测值的个数;3为未知参数的个数。设定卡方检验的误警概率[2]为10-3,则对于自由度为n-3的卡方检验,若其满足:
| $ T < \chi _{{\rm{TH}}}^2\left( {n - 3} \right) $ | (12) |
则认为卫星j求解的星历改正数是正确的,否则就会向用户发出告警。式(12)中的χTH2(n-3)为基于原假设分布,误警概率为10-3的分位值,即检测限值。
1.4 卫星星钟差分改正数求解在估计了卫星星历差分改正数之后,将式(9)、式(10)计算得到的星历差分改正数及其方差代入式(5),得到卫星j至参考站k之间的卫星钟差改正观测值及其方差为:
| $ \left\{ \begin{array}{l} z_{c, k}^j = \Delta \tilde \rho _k^j - \mathit{\boldsymbol{l}}_k^j\Delta {{\mathit{\boldsymbol{\hat R}}}^j} = \Delta {B^j} + v_k^j\\ \sigma _{z_{c, k}^j}^2 = (\mathit{\boldsymbol{l}}_k^j){\mathit{\boldsymbol{D}}_{\Delta {{\mathit{\boldsymbol{\hat R}}}^j}}}{(\mathit{\boldsymbol{l}}_k^j)^{\rm{T}}} + \sigma _{\Delta \tilde \rho _k^j}^2 \end{array} \right. $ | (13) |
多个参考站同时对卫星j进行观测,则可以建立多个如式(13)的观测方程。然后通过加权最小二乘解得卫星j的星钟差分改正数和对应的方差为:
| $ \left\{ \begin{array}{l} \Delta {{\hat b}^j} = {(\mathit{\boldsymbol{H}}_c^{\rm{T}}\mathit{\boldsymbol{D}}_c^{ - 1}{\mathit{\boldsymbol{H}}_c})^{ - 1}}\mathit{\boldsymbol{H}}_c^{\rm{T}}\mathit{\boldsymbol{D}}_c^{ - 1}{\mathit{\boldsymbol{z}}_c}\\ \sigma _{\Delta {{\hat b}^j}}^2 = {(\mathit{\boldsymbol{H}}_c^{\rm{T}}\mathit{\boldsymbol{D}}_c^{ - 1}{\mathit{\boldsymbol{H}}_c})^{ - 1}} \end{array} \right. $ | (14) |
式中,Hc为系数矩阵;Dc为由σzc, kj2组成的方差阵。与对轨道的完备性监测一样,广域增强系统对钟差改正也进行故障监测,在这里,本文仍然采用基于卡方分布的假设检验方法。
2 程序设计流程本文设计的广域增强系统星历及星钟差分改正数程序主要包括数据预处理、接收机钟差解算、星历差分改正数解算和故障监测、星钟差分改正数解算和故障监测等,其具体的程序流程如图 1所示。
 |
| 图 1 星历及星钟差分改正数解算程序流程 Fig.1 Correction Calculation Process of Satellite Ephemeris and Clock Error |
在解算卫星星历及星钟差分改正数的过程中,出现下面任何一种情况,则认为该卫星不可用,此时会向用户播发卫星不可用完备性指标:①星历差分改正数解算结果:max(abs(Δx, Δy, Δz))>127.875 m; ②星历卡方检验没有通过;③星钟差分改正数解算结果:ΔB > 255.875 m或ΔB < -256.0 m; ④星钟卡方检验没有通过。
只有当以上所有情况都没有发生时,才认为程序求解的改正数是有效的,系统会将这些差分改正数及相应的完备性信息播发给用户。需要说明的是,对于星历和星钟差分改正数设置的限值,一方面是由于播发带宽的限制;另一方面是为了减小值对观测误差的放大作用[5]。
3 实验分析为了验证差分改正和故障监测的有效性,本文编程实现了GPS广域增强系统的基本算法,并做了以下3个实验来分析差分定位的精度以及卫星在故障情况下的完备性监测:①单频差分定位精度分析;②卫星星历故障情况下的完备性监测;③卫星钟差故障情况下的完备性监测。
本文计算星历及星钟差分改正数的观测数据来源于美国连续运行参考站(continuously operating reference stations, CORS)[15]观测数据,测站分布如图 2中的五角星所示,共17个分布较均匀的测站,其中ARHR测站为主控站。上述3个实验的星历数据来源于MGEX发布的广播星历,观测数据是基于GPSL1信号单频伪距观测数据,卫星截止高度角为5°,对流层采用SBAS对流层模型进行改正,电离层采用CODE发布的格网模型进行改正,定位时采用本文计算的差分改正数进行星历和星钟误差改正。
 |
| 图 2 参考站分布图 Fig.2 Distribution Map of Reference Stations |
3.1 差分定位精度分析
为了分析差分定位的精度,本文选取了3个不同位置的用户(如图 2中圆圈所示,KYTE、ZMP1和AMC2)来验证差分改正结果。图 3给出了AMC2站的2016年年积日为183~189共7天的每个小时在E、N和U方向的误差均值。其中实线为单点定位的结果,虚线为利用了差分改正的定位的结果。
 |
| 图 3 AMC2测站的定位误差序列 Fig.3 Positioning Error Series of AMC2 Station |
从图 3中可以看出相对于单点定位的结果,差分定位的结果更加的平滑,精度也更高。测站KYTE和测站ZMP1的定位结果从时间序列图上看与测站AMC2的定位结果类似,因此,限于篇幅不再给出。
为了更加直观地表示精度信息,本文将3个测站共一周的单点定位与差分定位误差的95%值进行了统计。图 4给出了这3个测站每一天的E、N和U方向的95%统计值。
 |
| 图 4 测站定位误差日95%统计值 Fig.4 Positioning Error Daidly 95% Value of Stations |
从图 4中可以看出,AMC2和KYTE两个测站利用差分改正信息的定位精度95%统计值在水平方向大约为0.8 m,在高程方向为2.0 m,相较于单点定位提高了60%,但ZMP1测站上的差分定位精度95%统计值在水平方向为1.7 m,在高程方向为3.0 m,较单点定位提高较少,约为30%左右。ZMP1测站上的差分定位精度提高较小的原因是该测站位于整个广域增强系统监测区域的边缘,而边缘区域的监测站分布不均匀,其几何强度较弱,导致轨道的差分改正信息在边缘部分的改正能力下降,从而影响了其定位的精度。从整体上看,本文解算的差分改正数精度可以满足CAT Ⅰ类精密进近95%统计值水平方向16.0 m,垂直方向4.0 m的精度要求。
3.2 卫星星历故障情况下的差分改正和完备性监测为了验证卫星星历故障情况下的完备性监测效果,本文选择了2016年8月16号GPS PRN 30号卫星的广播星历进行试验。这颗卫星在13:59:44~16:00:00这一时间段播发的广播星历的卫星健康标识svh≠0,表示卫星处于不健康的状态。为了分析此算法对故障的探测能力,假设此时卫星的健康标识为svh=0对此段时间的广播星历进行差分改正计算并进行故障监测,来检验本算法能否有效地进行故障监测并及时发出警告。图 5给出了从10:00:00~16:00:00的星历差分改正结果;图 6为对应的卫星星历差分改正数卡方检验时间序列。
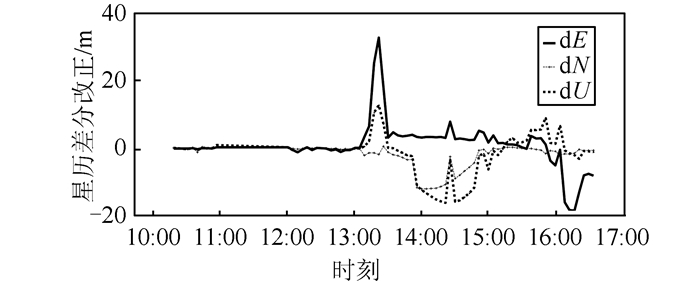 |
| 图 5 G30卫星星历差分改正数时间序列 Fig.5 Satellite Ephemeris Differential Correction Time Series of G30 |
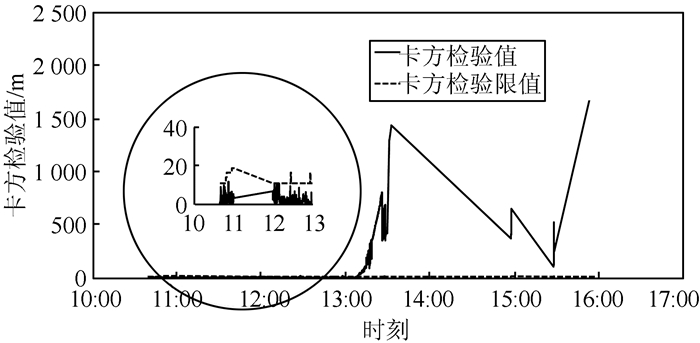 |
| 图 6 G30卫星星历差分改正数卡方检验时间序列 Fig.6 Chi Square Test Time Series of G30 Satellite Ephemeris Correction |
从图 5中可以看到,30号卫星星历差分改正数在10:00:00~13:00:00这一时间段变化比较平稳,且图 6对应的时间段(圆圈的放大部分)的故障检验值小于检测限值;在13:00:00~16:30:00这一时间段计算得到的差分改正数较大,变化也没有规律,对应的卡方检验值从13:07:50开始大于检测限值,表明广域增强系统的差分改正不具有完备性,应向用户发出警告。本文的故障检测发出告警时间与卫星被标定不健康的时间基本一致,表明能够有效地发现故障并发出告警。
3.3 卫星钟差故障情况下的差分改正和完备性监测卫星钟差故障常表现为台阶类(step-type)和斜坡类(ramp-type)故障两种[2]。台阶类故障是由于卫星钟差发生突变导致,而斜坡类卫星故障是由于卫星钟差按一定速度的缓慢变化导致。本文针对卫星斜坡类故障进行分析。
为了模拟卫星钟差斜坡类故障,本文同样将GPS PRN 13号卫星星历中的钟漂参数从-2.501 110 429 876×10-12改为-1.025 011 104 298×10-10,减小了约0.1 ns/s。
图 7给出了本文计算得到的从1~6 am的钟差差分改正数。可以看出,PRN 13号卫星在03:00:00~05:00:00时间段呈现一个斜坡类的上升趋势(图 7(a)),其变化率大概为0.03 m/s(图 7(b)),这准确地反映出了模拟故障时被改变的钟漂参数(1 ns/s)。图 8给出了与之对应的故障检测结果。结果表明此差分改正通过了卡方检验,差分结果可用,提高了系统的可用性。
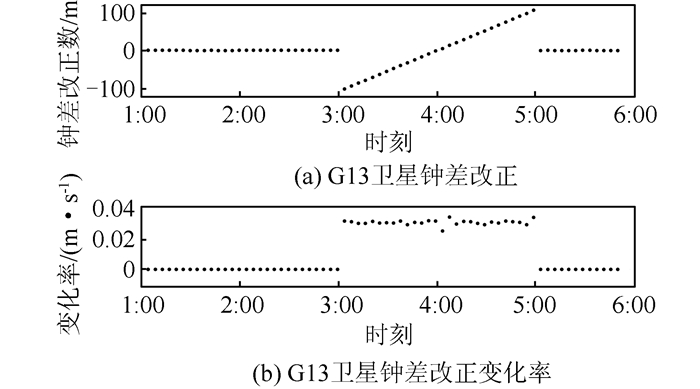 |
| 图 7 G13卫星钟改正数及其变化率 Fig.7 Satellite Clock Corrections and Its Rate of Change of G13 |
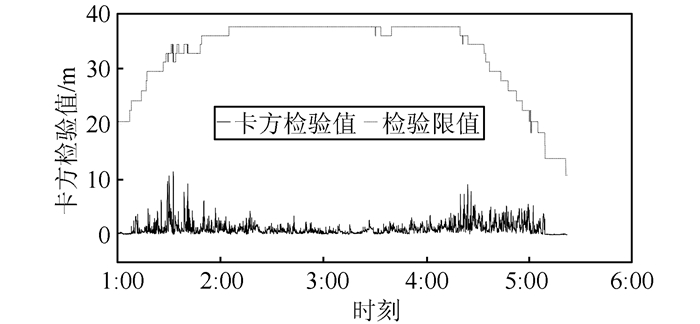 |
| 图 8 G13卫星钟斜坡类故障卡方检验时间序列 Fig.8 Chi-Squre Time Series of G13 Satellite Clock Ramp-Type Failure |
此外,还对此解算结果在用户端进行了验证。图 9给出了用户端的单点定位结果。
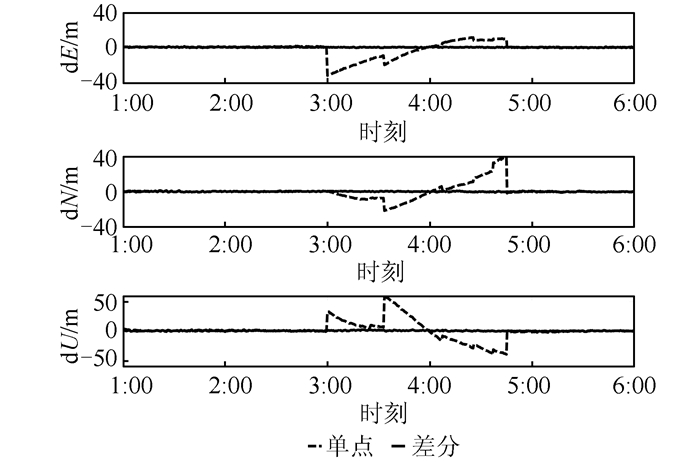 |
| 图 9 AMC2测站卫星钟斜坡类故障情况下单点定位与差分定位误差时间序列 Fig.9 Single Point Positioning and Differetial Positioning Error Time Series of AMC2 Station Under Clock Ramp-Type Failure |
由图 9可知,用户端的单点定位误差较大,尤其是U方向上的误差达到50 m左右;而利用差分改正信息的定位误差均在1 m以内。这表明了差分改正为用户提供了精确的卫星钟差及钟漂改正数,得到准确的定位结果。
4 结束语本文研究并实现了GPS广域增强系统的差分改正和故障监测算法,选择位于北美区域的17个监测站对GPS卫星实施差分改正和故障监测,就此系统从用户定位精度和故障检测能力上开展了分析,结果表明:①利用这些差分改正数所进行的单频差分定位较标准的伪距单点定位提高了60%,本文的差分改正数精度可以满足CATI精密进近的精度要求;②在卫星星历故障的情况下,本文方法能够很好地识别出故障卫星,并发出告警信息,减少了导航的完备性风险;③在卫星钟斜坡类故障情况下,不仅能够计算出有效的差分改正数,并能够准确地估计其变化率。
| [1] |
高为广, 楼益栋, 刘杨, 等. 卫星导航系统差分增强技术发展研究[J]. 测绘科学, 2013, 38(1): 51-53. DOI:10.3969/j.issn.1673-6338.2013.01.012 |
| [2] |
刘经南, 葛茂荣. 广域差分GPS的数据处理方法及结果分析[J]. 测绘工程, 1998, 7(1): 1-5. |
| [3] |
Tsai Y J. Wide Area Differential Operation of the Global Positioning System: Ephemeris and Clock Algorithms[D]. Palo Alto, CA: Stanford University, 1999
|
| [4] |
Chao Y C. Real Time Implementation of the Wide Area Augmentation System for the Global Positioning System with an Emphasis on Ionospheric Modeling[D]. Palo Alto, CA: Stanford University, 1997
|
| [5] |
李孝辉, 蔡成林, 吴海涛, 等.广域差分系统星钟和星历误差修正新方法研究[C].第一届中国卫星导航学术年会, 北京, 2010
|
| [6] |
蔡成林, 李孝辉, 吴海涛. 广域差分新方法的定位性能与差分网优化布局[J]. 宇航学报, 2009, 30(4): 1404-1409. DOI:10.3873/j.issn.1000-1328.2009.04.016 |
| [7] |
Chen J, Huang Z, Li R. Computation of Satellite Clock-Ephemeris Corrections Using a Priori Know-ledge for Satellite-Based Augmentation System[J]. GPS Solutions, 2017, 21(2): 663-673. DOI:10.1007/s10291-016-0555-8 |
| [8] |
陈金平. GPS完善性增强研究[D].郑州: 信息工程大学, 2001
|
| [9] |
秘金钟, 李毓麟. 广域差分GPS用户站的完备性监测[J]. 测绘通报, 2001(4): 6-8. DOI:10.3969/j.issn.0494-0911.2001.04.003 |
| [10] |
Walter T. WAAS MOPS: Practical Examples[C]. The 12th National Technical Meeting of the Institute of Navigation, Nashville, TN, 1999
|
| [11] |
Shallberg K, Sheng F S F. WAAS Measurement Processing: Current Design and Potential Improvements[C]. Position, Location and Navigation Symposium, IEEE, Monterey, CA, USA, 2008
|
| [12] |
Wu T, Peck S. An Analysis of Satellite Integrity Monitoring Improvement for WAAS[C]. The 15th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 2002
|
| [13] |
Walter T, Blanch J, Enge A P. L1/L5 SBAS MOPS to Support Multiple Constellations[C]. The 25th International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville, TN, USA, 2012
|
| [14] |
Hebelbarth A, Wanninger L. SBAS Orbit and Satellite Clock Corrections for Precise Point Positioning[J]. GPS Solutions, 2013, 17(4): 465-473. DOI:10.1007/s10291-012-0292-6 |
| [15] |
Liang L, Chun J, Lin Z, et al. Real-Time Single Frequency Precise Point Positioning Using SBAS Corrections[J]. Sensors, 2016, 16(8): 1261. DOI:10.3390/s16081261 |
| [16] |
王敬, 赵军祥. Blewitt周跳探测方法的改进[J]. 飞行器测控学报, 2011, 30(2): 80-83. |
 2019, Vol. 44
2019, Vol. 44

