| 惯导辅助的单频动态周跳探测 |
RTK-GPS(real-time kinematic GPS)是卫星定位领域最为精准的定位技术之一,利用载波相位双差观测值可以在城市环境下达到cm级精度,且已经广泛应用在诸多领域[1, 2]。近年来,一些学者尝试将该技术应用在移动车辆中[3, 4]。在城市环境观测条件较好时,完全可以达到理论精度,然而,城市环境复杂多变,当进入城市峡谷等不理想环境时,将发生信号频繁失锁、信噪比低、模糊度固定率低等诸多情况,其中一个很重要的原因就是周跳。周跳是载波相位的突然跳变,若周跳未被有效探测,将使得以载波为基础的RTK算法精度显著降低,因而城市RTK一个重要的技术难点就是克服周跳的问题。
在车载移动导航中,惯性导航系统(inertial navigation system,INS)经常与GPS/GNSS(global navigation satellite system)组合以提高导航的可靠性与精度[5-7]。在组合导航系统中,INS经常用来获取GPS失锁时汽车的位置、速度信息。城市环境下GPS信号质量不高,INS在提供位车辆速度的同时也为GPS提供了位置参照,借助该参照为GPS周跳探测提供了一种有效手段。由于车载应用多为消费级产品,受成本限制导航芯片多为单系统、且仅为单频,因而单系统单频的动态周跳探测是亟待解决的问题。
文献[8]利用之前已经固定的模糊度与当前模糊度作差获得检验量;文献[9]采用类似新息滤波的方法,以新息及其方差为探测依据;文献[10]根据惯导辅助PPP(precise point positionzing)算法,将双频系数(1, -1)和(4, -5)的结合起来探测具体频点的周跳。现有惯性辅助周跳方法均未对探测检验量的误差特性进行系统分析,未能揭示INS误差对探测性能的具体影响,探测阈值的估计方法缺乏针对性[9-11]。为克服以上问题,本文将IMU (inertial measurement unit)与GPS组合在一起,并采用三差观测方程和滑动窗口动态阈值方法,进行周跳探测,并进行动态实验以论证算法的有效性。
1 惯导辅助周跳探测算法GPS-RTK/INS组合导航系统中无论采用何种耦合方式,惯性辅助周跳探测的原理都是相同的。基于扩展卡尔曼滤波(extended Kalman filter,EKF)将GPS观测信息和INS观测信息融合后进行误差估计,而周跳探测则在量测更新前进行[4]。
1.1 惯性辅助周跳探测检测量GPS-RTK载波双差方程为:
| $ \begin{array}{*{20}{c}} {\lambda \nabla \Delta \mathit{\Phi } = \nabla \Delta {\rho _I} - \lambda \nabla \Delta N - }\\ {\nabla \Delta {d_I} + \nabla \Delta {d_T} + {e_{\nabla \Delta \mathit{\Phi }}}} \end{array} $ | (1) |
式中,λ为载波信号波长;Φ为相位观测值;ρI为基于惯导预测位置生成的卫地距离;N为模糊度;dI为电离层延迟;dT为对流层延迟;
| $ \begin{array}{*{20}{c}} {\nabla \Delta \mathit{\Phi } - \nabla \Delta {\rho _I}/\lambda + \nabla \Delta N = }\\ { - \nabla \Delta {d_I}/\lambda + \nabla \Delta {d_T}/\lambda + {e_{\nabla \Delta \mathit{\Phi }}}} \end{array} $ | (2) |
式中,
| $ {T_{dd}} = \nabla \Delta \mathit{\Phi } - \nabla \Delta {\rho _I}/\lambda + \nabla \Delta {N_{{t_m}}} $ | (3) |
此时根据式(3)已经可以进行周跳判断,然而双差检测法不可避免地涉及已固定的模糊度问题,如果模糊度没有固定或较长时间不能固定都将导致算法失灵。本文利用三差方法进一步消除模糊度参数,而动态定位中的位置变化量则由惯性数据给出,下面给出三差方程:
| $ \begin{array}{*{20}{c}} {\delta \;\nabla \Delta \mathit{\Phi } = - \delta \nabla \Delta {\rho _I}/\lambda - \delta \nabla \Delta {d_I}/\lambda + }\\ {\delta \nabla \Delta {d_T}/\lambda + {e_{\delta \nabla \Delta \mathit{\Phi }}}} \end{array} $ | (4) |
则惯性辅助三差周跳检测量为:
| $ \begin{array}{*{20}{c}} {D{T_{dd}} = \delta \;\nabla \Delta \mathit{\Phi }/\lambda - \delta \nabla \Delta {\rho _I}/\lambda = }\\ {\delta \;\nabla \Delta \mathit{\Phi }/\lambda - \delta \nabla {\rho _I}/\lambda + \delta \nabla \rho /\lambda } \end{array} $ | (5) |
采用历元间差分的方式可以削弱INS位置误差对周跳探测的影响。此外由于动态解算中长时间滤波下的方差已经很小,解算精度很高,与固定后方差相差无几,不必刻意追求以固定解为开始,以任意浮点解开始更具有一般性和普适性, 即使模糊度在一段时间内无法固定,仍能进行有效探测。
1.2 周跳探测阈值的确定由于采用GPS三差方程,周跳检验量主要受INS位置变化量影响而非绝对位置影响,因而检测量与运动状态有关,当惯导误差持续增大时,必将引起周跳检测量的方差增加,此时算法将无法探测小周跳。综合考虑INS误差源和GNSS误差源的影响,采用滑动窗口内数据估计周跳探测的阈值,阈值估计充分反映INS误差影响,确定的阈值具有较强的自适应性。最后采用实测数据进行实验并验证了惯性辅助周跳探测方法的有效性。
检验量DTdd包括GNSS误差和INS误差的影响,若取4倍方差为阈值,要探测1周大小的周跳,以GPS L1信号为例,INS在一次三差内位置变化量误差小于4.76 cm,理论上才可以探测出所有周跳。然而,在实际应用过程中,INS误差受各种因素影响,包括上一历元误差、元器件误差、导航状态误差等,因而该误差在表现上不如GPS稳定。顾及这种变化误差的影响,采用滑动窗口的方式估计阈值做实时周跳探测。
DTdd包含GNSS三差噪声
| $ \begin{array}{*{20}{c}} {{T_{D{T_{dd}}}} = }\\ {\left\{ {\begin{array}{*{20}{c}} {4{\sigma _{D{T_{dd}}}}\left( {D{T_{dd}}} \right), \quad \max \left( {\left| {D{T_{dd}}} \right|} \right) \le 4{\sigma _\mathit{\Phi }}}\\ {4{\sigma _{D{T_{dd}}}}\left( {\left| {D{T_{dd}}} \right| > 4\sigma } \right), \max \left( {\left| {D{T_{dd}}} \right|} \right) > 4{\sigma _\mathit{\Phi }}} \end{array}} \right.} \end{array} $ | (6) |
式中,σDTdd(DTdd)表示利用所有窗口内小于GNSS噪声的数据估计阈值,而当INS误差较大时,采用满足|DTdd|>4σ的数据估计阈值。
2 算例实验与分析本文以紧组合算法为例简要介绍算法流程,主要包括惯导机械编排、惯导误差补偿、双差观测值生成、周跳探测、滤波反馈、Kalman滤波、LAMBDA算法等处理模块[12-14]。图 1给出了算法架构,由于在组合导航中无论采用何种耦合方式,惯性辅助周跳探测部分原理是相同的,松组合由于单独解算GPS,因而要在惯导辅助周跳探测时生成两次双差观测值,而紧组合则仅需一次。
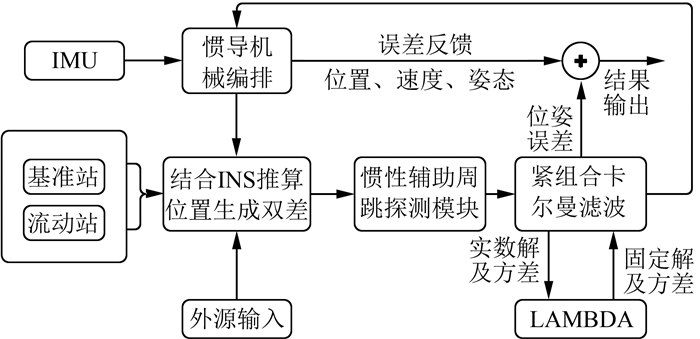 |
| 图 1 惯性辅助算法流程图 Fig.1 The Algorithm of INS-Aided Slip Cycle Detection |
为评估本文提出的单频实时动态周跳探测算法的性能,2017-11-24T13:43~16:43 (GPST:5:43~8:03)在湖北武汉大花岭进行了车载静态、动态实验,搭载了NovAtel的OEM系列接收机,IMU采样频率为200 Hz,性能指标为(0.75deg/h; 1 mg)。基准站采用Leica GRX1200GGPRO双频接收机,采样率为1 Hz,基站距离约为14 km。其中静态数据约15 min,动态数据约2 h,观测条件较好。本文将分别利用静态和动态数据进行周跳检测实验。
静态实验将检查静态阈值的缺陷性,静态观测一般为组合导航的初始对准阶段,该阶段会选择在GPS观测条件较好,地面平整的场地进行。此时,GPS数据显然应该具有更好的性能,同动态数据相比,传统方法的固定阈值探测周跳就存在漏探等问题。图 2为此次静态测量数据周跳检测结果。
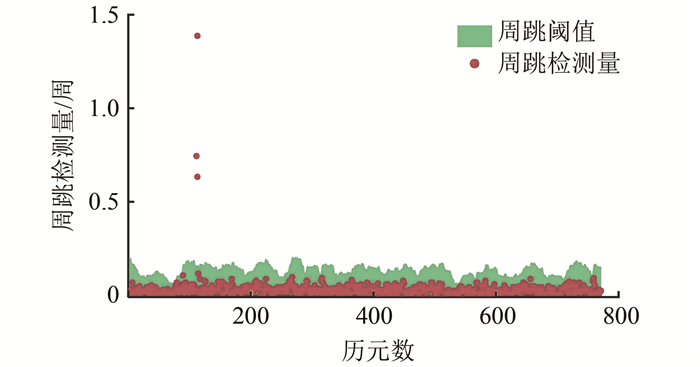 |
| 图 2 静态数据周跳检测结果 Fig.2 Slip Cycle Detection of Static Data |
图 2中,横坐标为时间以历元为单位,历元间隔为1 s,纵坐标为三差周跳检验量,单位是周。由图 2可以发现,在100 s左右历元有3个点明显在正常数据时间序列之外。传统方法一般以0.5或0.8为阈值,此处若以0.8为阈值进行探测,将不能发现另外两个周跳点;而若以0.5为阈值将会发现所有周跳,但是这显然不可行,在动态数据中,0.5的周跳探测阈值将造成灾难,下文动态实验将具体说明。
动态实验在开始和结尾时各静止约10 min,其余正常行驶。GPS信号质量不高时的位置漂移误差是反映GNSS/INS组合导航算法的关键指标[7, 8],为验证算法在长时间推算以及模糊度无法固定时的周跳探测性能,本文利用2 500到4 000共1 500历元(从6:25~6:55半小时)的数据进行实验,期间多为浮点解,这理应更能体现算法价值。
测试中发现,该组合算法因为采用单系统模式,虽多数情况共视卫星数大于等于5,然而仍出现仅有4颗星的情况,甚至分别于第2 705~2 706(GPST: 06:18:35~06:18:36)、4 491(GPST: 06:58:53)以及4 651~4 654历元(GPST: 07:01:33~07:01:36)出现仅有3颗共视卫星,RTK无法解算的情况。而此时仍可应用紧组合算法。可以发现数据采集时间较长,而Takasu等[9]将新息向量及其方差定义的周跳检测量用于卡尔曼滤波长时间估算,方差将会非常小,那么惯导的动态误差引起的周跳检测量增加将超过阈值引起错误;另外由于基线较长,固定结果并不理想,Lee等[8]提出的依靠上次固定的模糊度探测周跳的算法显然也存在问题。
本文实验数据由双频接收机采集,经解算双频RTK固定率在90%以上,平面内符合精度优于3 cm,可以认为参考准确,因而选择该结果为参考。图 3为组合导航结果与RTK结果作差得到的位置误差图。
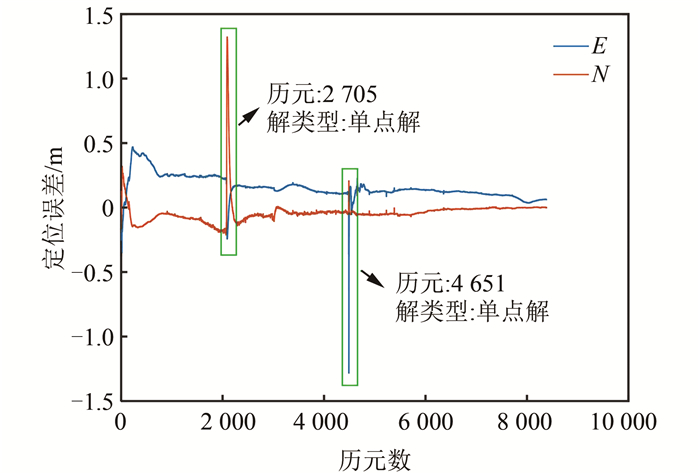 |
| 图 3 位置误差图 Fig.3 Horizontal Statistics Error of Trajectory |
从图 3可以发现,误差跳动最大的位置出现在2 705和4 651历元处,结合共视卫星数和位置精度衰减因子值发现,差别最大的地方在共视卫星仅为3颗的位置,与前文描述相符。在4 491历元处也出现单点解,标准差较大达到1.5 m,但并未出现滤波的位置跳动。对比RTK解算结果,RTK算法在这两个位置共视卫星不足,因而出现抖动。此差异体现了紧组合算法的优越性与正确性。
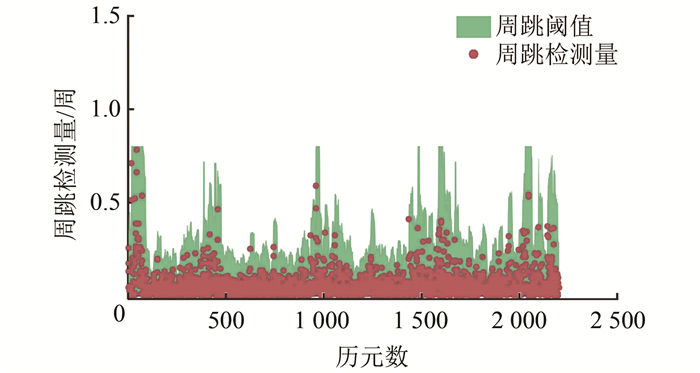
在GPS-RTK的组合导航中,INS的推算精度主要取决于陀螺精度,惯性设备精度应满足式(6),因而仍以1周的小周跳检验算法的精度与可靠性。原始数据已采用双频观测值Turbo-Edit方法进行验证,可以认为是“干净”的数据。现选取时段内高度角最高且没有周跳的15号卫星为参考星,21号卫星为流动星,它们构成双差观测值,向L1载波每隔30 s人为增加1周周跳,探测周跳过程中窗口长度为20 s,码噪声取0.02周。图 4为21号卫星原始观测序列,图 5为加入周跳后算法的探测结果。
 |
| 图 4 原始观测序列 Fig.4 Raw Observations |
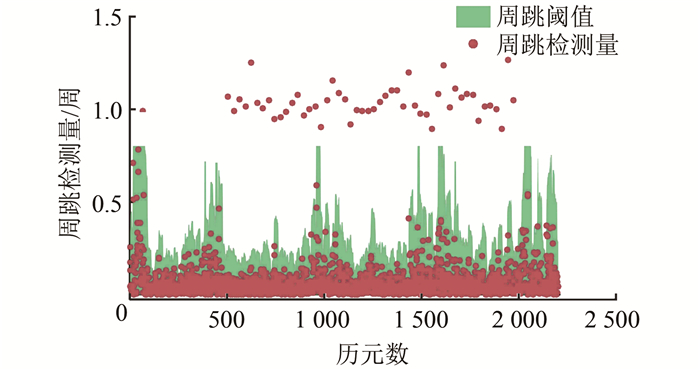 |
| 图 5 加入周跳后序列 Fig.5 Observations After Adding Cycle Slips |
图 4、图 5中坐标轴与内容含义与前文相同。可清楚发现在历元数500处开始每30 s人为加入大小为1周的周跳,本文认为算法对小周跳敏感,且没有漏探、错探的情况出现。结合以上结果和静态数据结果可以得出以下结论。
1) 使用滑动窗口阈值的方法,在INS动态误差较大时采用较大的检测量,估计得到的阈值随INS误差变化而变化,具有较强的适应性。
2) 对于静态与动态数据,周跳检测量量级不同时,该算法均能进行有效探测,不会出现固定阈值时错探和漏探的情况。
3) 车载动态数据固定情况不理想时,在难以固定仅为浮点解的情况下仍能对1周的小周跳进行有效探测。
3 结束语为提高城市复杂环境下车载RTK-GPS算法的精度与可靠性,本文设计并实现了基于惯导辅助的实时单频动态周跳探测算法,绕过传统单频周跳探测时不可避免的伪距噪声、多普勒噪声问题,可以实现实时小周跳的探测,该算法能够有效利用惯导信息,基于滑动窗口的动态阈值估计能够同时顾及GNSS与惯导的误差。实验数据表明,本文方法在GNSS/INS误差较小时,可以很好地满足判定要求;而在惯导推算误差略大时,仍保持可靠性和敏感性。在车载动态实验中,1周的小周跳在三差检验量中是非常显著的,可以实现实时动态探测。
| [1] |
Meng X. Real-Time Deformation Monitoring of Bridges Using GPS/Accelerometers[D]. Nottingham: University of Nottingham, 2002 http://www.researchgate.net/publication/37245649_Real-time_deformation_monitoring_of_bridges_using_GPSAccelerometers
|
| [2] |
Chiang K W, Tsai M L, Chu C H. The Development of an UAV Borne Direct Georeferenced Photogrammetric Platform for Ground Control Point Free Applications[J]. Sensors, 2012, 12(12): 9161-9180. |
| [3] |
唐炉亮, 杨雪, 牛乐, 等. 一种众源车载GPS轨迹大数据自适应滤选方法[J]. 测绘学报, 2016, 45(12): 73-81. |
| [4] |
Petovello M G. Real-Time Integration of a Tactical-grade IMU and GPS for High-Accuracy Positioning and Navigation[D]. Calgary: University of Calgary, 2005
|
| [5] |
Niu X, Zhang H, Shi C, et al. A Proposed Evaluation Standard for Navigation Results of MEMS INS/GPS Integrated System[C]. The 2010 International Symposium on GPS/GNSS, Taipei, China, 2010
|
| [6] |
Niu X, Zhang Q, Gong L, et al. Development and Evaluation of GNSS/INS Data Processing Software for Position and Orientation Systems[J]. Survey Review, 2015, 47(341): 87-98. DOI:10.1179/1752270614Y.0000000099 |
| [7] |
李团, 章红平, 牛小骥, 等. RTK/INS紧组合算法在卫星数不足情况下的性能分析[J]. 武汉大学学报·信息科学版, 2018, 43(3): 478-484. |
| [8] |
Lee H K, Wang Jinling, Rizos C. Carrier Phase Processing Issues for High Accuracy Integrated GPS/Pseudolite/INS Systems[C]. Proceedings of 11th IAIN World Congress, Berlin, Germany, 2003
|
| [9] |
Takasu T, Yasuda A. Cycle Slip Detection and Fixing by MEMS-IMU/GPS Integration for Mobile Environment RTK-GPS[C]. Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, Savannah, USA, 2008
|
| [10] |
韩厚增.惯导辅助BDS/GPS高精度动态定位模型研究[D].徐州: 中国矿业大学, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10290-1017950201.htm
|
| [11] |
Godha S. Performance Evaluation of Low Cost MEMS-Based IMU Integrated with GPS for Land Vehicle Navigation Application[D]. Calgary: University of Calgary, 2006 http://www.researchgate.net/publication/272009386_performance_evaluation_of_low_cost_mems-based_imu_integrated_with_gps_for_land_vehicle_navigation_application
|
| [12] |
仇立成, 姚宜斌, 祝程程. GPS/INS松组合与紧组合的实现与定位精度比较[J]. 测绘地理信息, 2013, 38(3): 17-19. |
| [13] |
宋宇, 朱锋, 卢立果, 等. 车载GNSS/SINS组合导航中零速区间探测方法的改进[J]. 测绘地理信息, 2016, 41(6): 12-16. |
| [14] |
刘帅. 模糊度固定解PPP/INS紧组合理论与方法[J]. 测绘学报, 2017, 46(6): 803. |
 2020, Vol. 45
2020, Vol. 45

